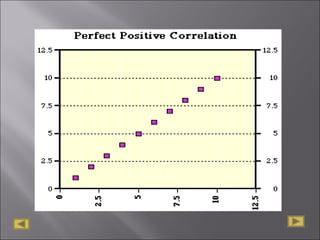
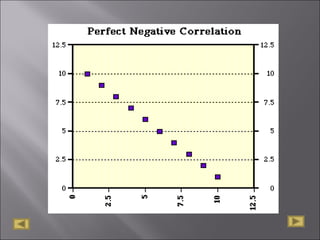
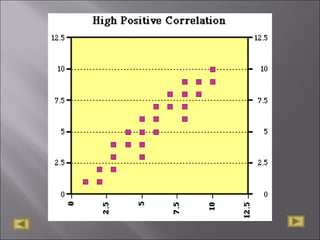
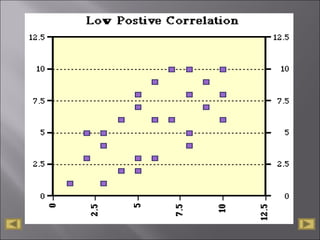
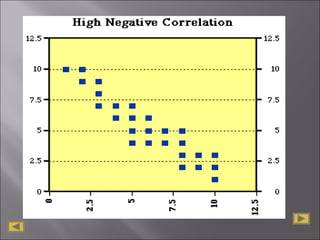
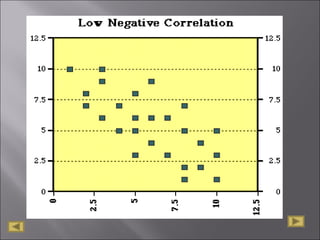
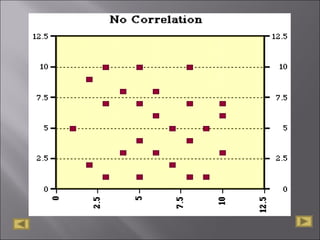
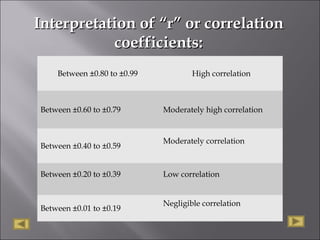
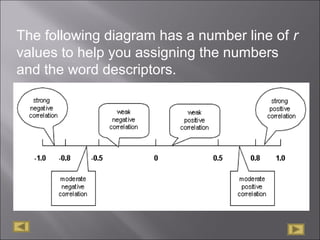
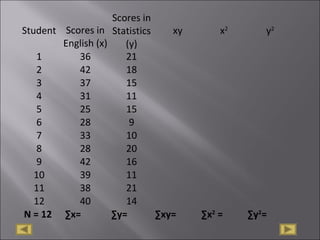
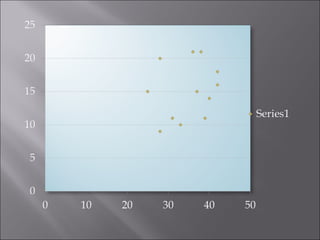
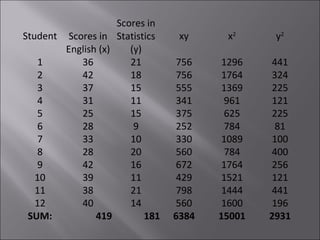
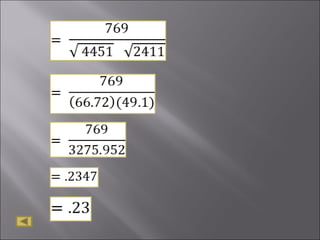
The document discusses correlation analysis and correlation coefficients. It explains that correlation analysis finds how well data points fit a line of best fit, with perfect correlation being 1. The correlation coefficient r is a measure of the linear relationship between two variables, ranging from -1 to 1. A scattergram plots the variables to show the strength, shape, direction, and outliers of their relationship. The interpretation of r values is provided, with higher absolute values indicating stronger correlation. Steps for correlation analysis and an example are also presented.

2. Correlation AnalysisCorrelation Analysis is the
process of finding how well
(or badly ) the line fits the
observations, such that if all
the observations lie exactly
on the line of best fit, the
correlation is considered to
be perfect 1 or unity.

3. Correlation CoefficientCorrelation Coefficient ( R )( R ) or
the Pearson’s product moment
correlation coefficient in honor
of its developer Karl Pearson ).
It is numerical measure of the
linear relationship between two
variables usually labeled x and
y.

4. ScattergramScattergram is composed of the points
plotted in the rectangular coordinate
system, where x and y are respectively the
values of the independent and dependent
variables. It is useful when there are a large
number of data sets. They provide the
following information about the
relationship between two variables:
•Strength
•Shape – linear, curved, etc.
•Direction
•Presence of outliers

12. Interpretation of “r” or correlationInterpretation of “r” or correlation
coefficients:coefficients:
Between ±0.80 to ±0.99 High correlation
Between ±0.60 to ±0.79 Moderately high correlation
Between ±0.40 to ±0.59
Moderately correlation
Between ±0.20 to ±0.39 Low correlation
Between ±0.01 to ±0.19
Negligible correlation

13. r

14. The correlation coefficient, r, has a
specific range of values:

15. Note that:
•r never lies outside this range, therefore r = 2 is a
nonsense answer whose only explanation can be "I
made an arithmetic error".
•r =1 is perfect positive correlation and all the data
points lie exactly on a straight line with positive
gradient.
•r = -1 likewise is perfect negative correlation.
•r is often measured or referred to as a percentage.
In this case, the range is from -100% to 100%
(remembering that 100% is the same as 1)

16. Steps you need to follow:
1.draw the scatterplot;
2.draw the trend line which describes
the direction of the data;
3.evaluate how closely the cloud of data
points clusters around the line;
4.determine what r value and what word
descriptor best suits the data cloud.

17. The following diagram has a number line of r
values to help you assigning the numbers
and the word descriptors.

18. Student Scores in
English (x)
Scores in
Statistics
(y)
xy x2
y2
1 36 21
2 42 18
3 37 15
4 31 11
5 25 15
6 28 9
7 33 10
8 28 20
9 42 16
10 39 11
11 38 21
12 40 14
N = 12 ∑x= ∑y= ∑xy= ∑x2
= ∑y2
=

20. Student Scores in
English (x)
Scores in
Statistics
(y)
xy x2
y2
1 36 21 756 1296 441
2 42 18 756 1764 324
3 37 15 555 1369 225
4 31 11 341 961 121
5 25 15 375 625 225
6 28 9 252 784 81
7 33 10 330 1089 100
8 28 20 560 784 400
9 42 16 672 1764 256
10 39 11 429 1521 121
11 38 21 798 1444 441
12 40 14 560 1600 196
SUM: 419 181 6384 15001 2931