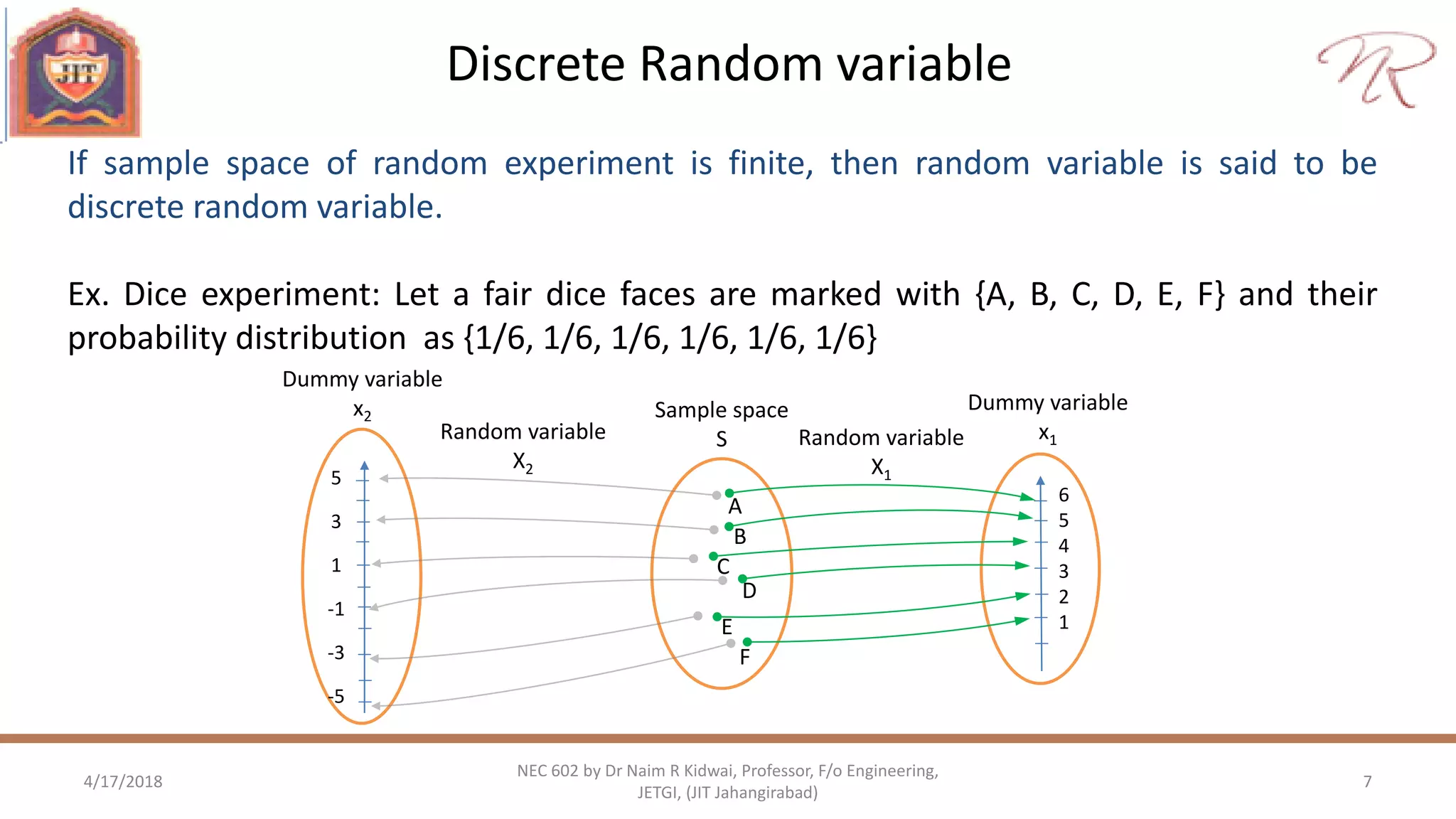
The document focuses on the concepts of probability, random variables, and statistical averages, exploring the foundational principles of random processes. Key topics include the definition and properties of probability, Bayes' theorem, types of random variables (discrete and continuous), cumulative and probability density functions (CDF and PDF), as well as joint and marginal distributions. The document emphasizes the mathematical representation of these concepts, illustrated through examples such as dice experiments and transformations of random variables.













![Statistical Averages: mean
4/17/2018 15
NEC 602 by Dr Naim R Kidwai, Professor, F/o Engineering,
JETGI, (JIT Jahangirabad)
Pdf and cdf provide probabilistic characterization of random variable. Partial
description of random variable are given in form of statistical averages.
[ ] ( )
Let ( ), where X, Y random variables
then [ ] ( ) ( )
X X
Y X
E X xf x dx
Y g X
E Y g x f x dx
Average or Mean or Expectation:](https://image.slidesharecdn.com/nec602unitiirandomprocess-180417054415/75/Nec-602-unit-ii-Random-Variables-and-Random-process-15-2048.jpg)
![Statistical Averages: Moment and central moment
4/17/2018 16
NEC 602 by Dr Naim R Kidwai, Professor, F/o Engineering,
JETGI, (JIT Jahangirabad)
nth central moment
th
st
nd 2
n moment of random variable
[ ] ( )
1 moment [ ] mean
2 moment [ ] mean square
n n
XE X x f x dx
E X
E X
nth moment
th
st
nd 2 2 2 2
2
n central moment of random variable
[( ) ] ( ) ( )
1 central moment [( )] 0
2 moment [( ) ] [ ]
Variance of X,
standard deviation of X
n n
X X X
X
X X X
X
X
E X x f x dx
E X
E X E X
](https://image.slidesharecdn.com/nec602unitiirandomprocess-180417054415/75/Nec-602-unit-ii-Random-Variables-and-Random-process-16-2048.jpg)
![Statistical Averages: Joint Moments
4/17/2018 17
NEC 602 by Dr Naim R Kidwai, Professor, F/o Engineering,
JETGI, (JIT Jahangirabad)
,order i+j moment, [ ] ( , )
If X and Y are statistically independent then [ ] [ ] [ ]
i j i j
X Y
i j i j
E X Y x y f x y dxdy
E X Y E X E Y
Order i+j moment : Let X and Y are random variables with joint pdf fX,Y(x,y)
Correlation: E[XY] is referred as correlation
Covariance: COV[XY]=E[(X-X) (Y-Y)] = E[XY] - X Y is referred as covariance of X and Y
[ ]
Correlation coefficient,
1 1
0 no correlation,
1 Y and X are linearly dependent
XY
X Y
XY
XY
XY
Cov XY
](https://image.slidesharecdn.com/nec602unitiirandomprocess-180417054415/75/Nec-602-unit-ii-Random-Variables-and-Random-process-17-2048.jpg)


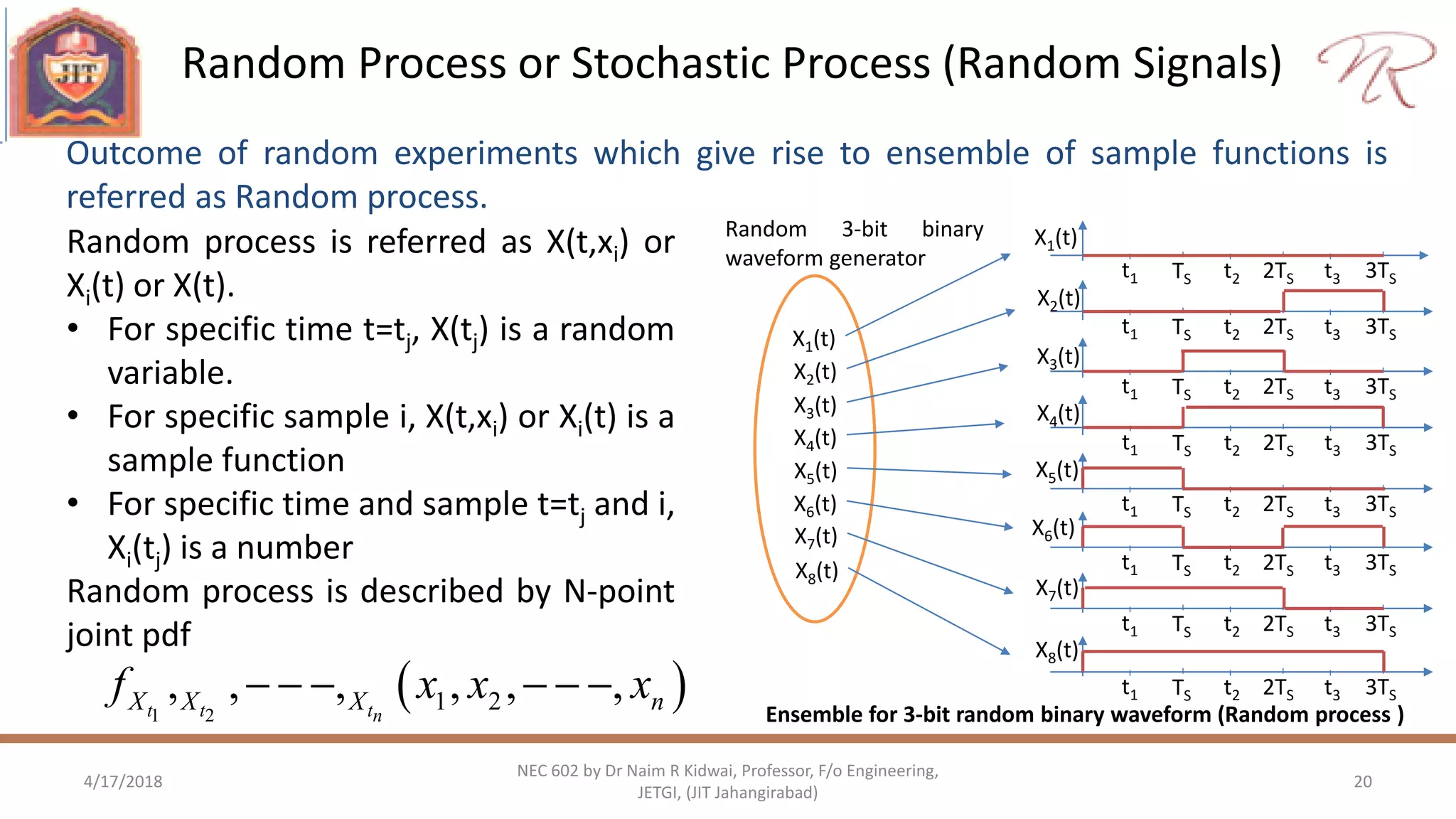
![Random Process : Important moments
4/17/2018 21
NEC 602 by Dr Naim R Kidwai, Professor, F/o Engineering,
JETGI, (JIT Jahangirabad)
A random process is partially characterized by statistical averages or moments
1
( ) 1 1 1[ ( )] ( )tX t XE X t x f x dx
Mean or Expectation of X(t):
Variance of X(t)
1
22
2
1 1 1t
X X
X X
t E X t t
x t f x dx
• Mean of random process is generally function of time
• Variance & standard deviation of random process is generally function of time](https://image.slidesharecdn.com/nec602unitiirandomprocess-180417054415/75/Nec-602-unit-ii-Random-Variables-and-Random-process-21-2048.jpg)





