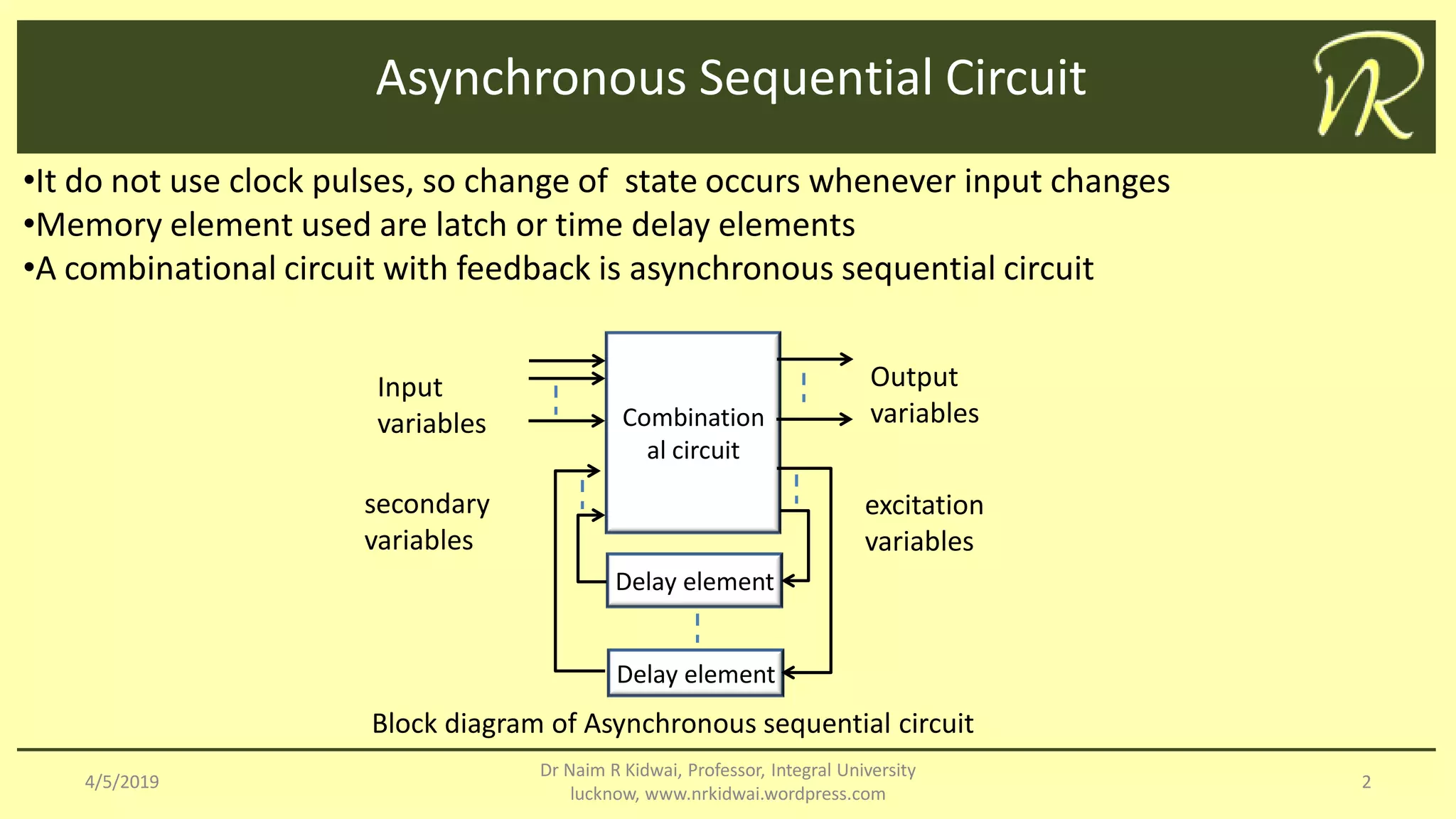
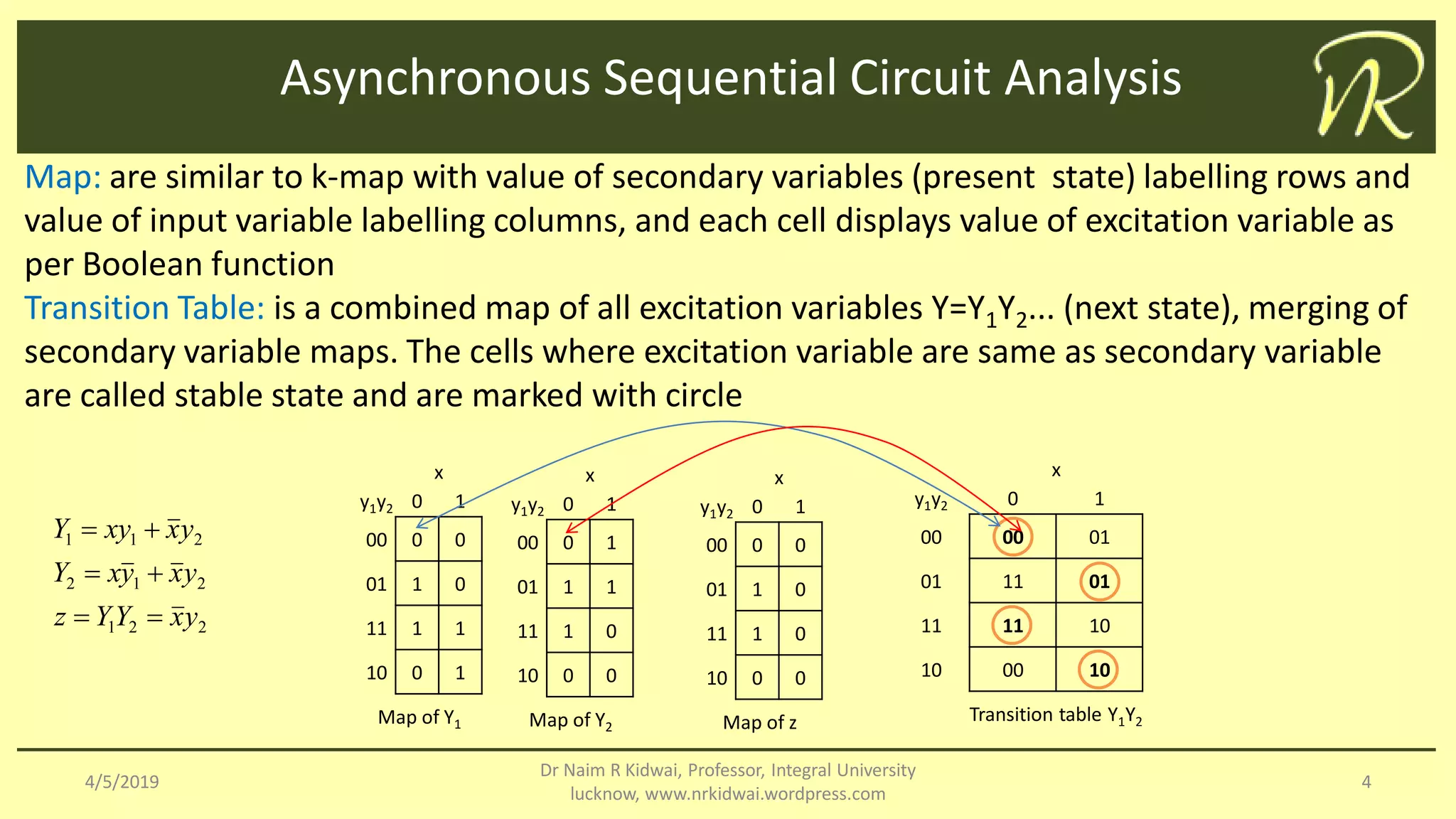
The document outlines the analysis and design of asynchronous sequential circuits, which operate without clock pulses and use feedback combinations of memory elements like latches. It discusses methodologies such as transition and flow tables to describe circuit behavior and highlights the significance of mapping states and variables. Additionally, it addresses race conditions, categorizing them as critical or non-critical based on the dependency of final stable states on the order of state changes.

1. Asynchronous Sequential Circuit Analysis
4/5/2019
Dr Naim R Kidwai, Professor, Integral University
lucknow, www.nrkidwai.wordpress.com
1
Learning Objectives:
1. To learn analysis of asynchronous Sequential Circuits
2. To learn map, transition table and flow table
3. To learn Design of asynchronous Sequential Circuit
4. To race conditions in asynchronous Sequential Circuit

2. Asynchronous Sequential Circuit
4/5/2019
Dr Naim R Kidwai, Professor, Integral University
lucknow, www.nrkidwai.wordpress.com
2
•It do not use clock pulses, so change of state occurs whenever input changes
•Memory element used are latch or time delay elements
•A combinational circuit with feedback is asynchronous sequential circuit
Combination
al circuit
Delay element
Delay element
Input
variables
secondary
variables
excitation
variables
Output
variables
Block diagram of Asynchronous sequential circuit

3. Asynchronous Sequential Circuit Analysis
4/5/2019
Dr Naim R Kidwai, Professor, Integral University
lucknow, www.nrkidwai.wordpress.com
3
Steps of Analysis
1. In the circuit look for feedback
2. Assign excitation variable to output that is fed-back (Capital Letter)
3. Assign secondary variable at the input where feedback ends (small letters)
4. Write the Boolean expression for excitation variable
221
212
211
yxYYz
yxyxY
yxxyY



y1
y2
Y2
Y1
z
x
The circuit in example
has two feedback
paths Input
variable
secondary
variable
excitation
variable

4. Asynchronous Sequential Circuit Analysis
4/5/2019
Dr Naim R Kidwai, Professor, Integral University
lucknow, www.nrkidwai.wordpress.com
4
x
y1y2 0 1
00 0 0
01 1 0
11 1 1
10 0 1
Map of Y1
Map: are similar to k-map with value of secondary variables (present state) labelling rows and
value of input variable labelling columns, and each cell displays value of excitation variable as
per Boolean function
Transition Table: is a combined map of all excitation variables Y=Y1Y2... (next state), merging of
secondary variable maps. The cells where excitation variable are same as secondary variable
are called stable state and are marked with circle
x
y1y2 0 1
00 0 1
01 1 1
11 1 0
10 0 0
Map of Y2
x
y1y2 0 1
00 00 01
01 11 01
11 11 10
10 00 10
Transition table Y1Y2
x
y1y2 0 1
00 0 0
01 1 0
11 1 0
10 0 0
Map of z
221
212
211
yxYYz
yxyxY
yxxyY




5. Asynchronous Sequential Circuit Analysis
4/5/2019
Dr Naim R Kidwai, Professor, Integral University
lucknow, www.nrkidwai.wordpress.com
5
x
y1y2 0 1
00 0 0
01 1 0
11 1 1
10 0 1
Map of Y1
Flow table: In the design representation of asynchronous sequential circuit it is more
convenient to represent the state with letter symbols rather than binary symbols. Such a
table is referred as flow table.
Output may be included in flow /transition table with state separated by a comma, giving
complete description of the circuit
x
y1y2 0 1
00 0 1
01 1 1
11 1 0
10 0 0
Map of Y2
x
y1y2 0 1
00 00 01
01 11 01
11 11 10
10 00 10
Transition table Y1Y2
x
y1y2 0 1
00 0 0
01 1 0
11 1 0
10 0 0
Output Map (z)
x
y1y2 0 1
a a, 0 b, 0
b c, 1 b, 0
c c, 1 d, 0
d a, 0 d, 0
Flow table with output
221
212
211
yxYYz
yxyxY
yxxyY




6. Design from Flow table
4/5/2019
Dr Naim R Kidwai, Professor, Integral University
lucknow, www.nrkidwai.wordpress.com
6
00 01 11 10
a a , 0 a , 0 a , 0 b , 0
b a , 0 a , 0 b , 1 b , 0
Flow table with output
1. The circuit has two input variables (let x1 and x2), one
excitation variable Y (corresponding secondary variable y)
and one output z.
2. Assign binary values to state . a=0, b=1, then flow table
changes to transition table with outputx1x2
y 00 01 11 10
0 0 , 0 0 , 0 0 , 0 1 , 0
1 0 , 0 0 , 0 1 , 1 1 , 0
transition table with output
3. Separate map of Y and output map and find binary expression
for Y and z using k map
4. Implement the Boolean expressions using gates
x1x2
y 00 01 11 10
0 0 0 0 1
1 0 0 1 1
Map of Y
x1x2
y 00 01 11 10
0 0 0 0 0
1 0 0 1 0
Output map
yxxxY 121  yxxY 21
y
x2
Y
z
x1

7. Race Conditions
A race condition exists when two or more state variables (excitation) change in response to
input variable changes.
Non critical race: if final stable state does not depend on the order of state variable changes
Critical race: if final stable state depends on the order of state variable changes
4/5/2019
Dr Naim R Kidwai, Professor, Integral University
lucknow, www.nrkidwai.wordpress.com
7
x
y1y2 0 1
00 00 11
01 10 11
11 01 11
11 00 01
Non critical race
Y1Y2=00, and x=0 to x=1
then possible transitions are
Y1Y2: 00→11
Y1Y2: 00→01 →11
Y1Y2: 00→10 →01 →11
x
y1y2 0 1
00 00 11
01 10 01
11 00 01
10 01 11
Non critical race
Y1Y2=00, and x=0 to x=1
then possible transitions are
Y1Y2: 00→11 →01
Y1Y2: 00→01
Y1Y2: 00→10 →11 →01
x
y1y2 0 1
00 00 11
01 10 01
11 00 11
10 01 10
Critical race
Y1Y2=00, and x=0 to x=1
then possible transitions are
Y1Y2: 00→11
Y1Y2: 00→01
Y1Y2: 00→10
x
y1y2 0 1
00 00 11
01 10 11
11 00 11
10 01 10
Critical race
Y1Y2=00, and x=0 to x=1
then possible transitions are
Y1Y2: 00→11
Y1Y2: 00→01 →11
Y1Y2: 00→10