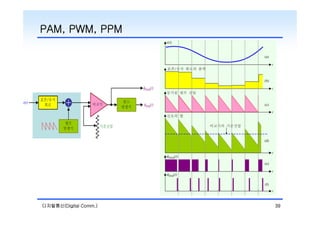
The document discusses pulse modulation techniques in digital communication. It introduces three main types of pulse modulation: PAM (Pulse Amplitude Modulation), PWM (Pulse Width Modulation), and PPM (Pulse Position Modulation). It then focuses on PAM modulation, discussing natural sampling and flat-top sampling. For natural sampling, it explains how the spectrum is periodic with harmonics determined by the sampling frequency. For flat-top sampling, it shows how the signal is reconstructed by filtering each sampled value. Proper filtering and equalization are needed to remove distortion from the band-limited sampling pulse.

1. 펄스 변조(Pulse Modulation)
조선대학교
정보통신공학과
디지털통신(Digital Comm.)

2. Contents
Sampling theory
Pulse Modulation
 PAM (Pulse Amplitude Modulation)
 PWM (Pulse Width Modulation)
 PPM (Pulse Position Modulation)
Multiplexing
 FDM
 TDM
디지털통신(Digital Comm.)
2

3. 기저대역 시스템 (Baseband system)
Digital
information
Information
source
Character
information
•PAM
•PWM
•PPM
PCM
Analog
information
Sampling
Quantization
Encoding
Pulse
modulation
형식화(Formatting)
Analog
information
Information
sink
LPF
Decoding
TX
Channel
Demodulation
/detection
RX
Character
information
Digital
information
형식화(Formatting) 및 기저대역(baseband) 신호 전송
디지털통신(Digital Comm.)
3

4. Sampling
참고 : http://www.engr.usask.ca/classes/EE/352/virtual_labs.htm
 Sampling theory
 Ideal sampling(=impulse sampling)
analog signal x(t ) has a bandwidth
x (t ) 
fm

  (t  nT )
n  
Ts :sampling period
s
x s ( t )  x ( t ) x ( t ) 

 x ( nT
n  
1
X  ( f )  F [ x  ( t )] 
Ts
s
) ( t  nT s )

(f
n  
fs 
1
X s ( f )  X ( f )* X  ( f ) 
Ts
디지털통신(Digital Comm.)

 nf s )
1
: sampling frequency
Ts

n  
X ( f  nf s )
4

5. Sampling
analog signal x(t ) has a bandwidth f m
| X (f)|
x ( t )
t
0
x (t ) 


n  
1
X ( f ) 
Ts
 ( t  nT s )
…
…
-4Ts -2Ts
2Ts 4Ts
0
0
2Ts 4Ts

(f
n
t
-2fs
 nf s )
…
…
-fs
x s (t )  x (t ) x (t )
-4Ts -2Ts
f
-fm 0 fm
0
f
2fs
fs
| X (f)|
t
…
…
-2fs
-fs
0
fs
2fs
f
Impulse sampling
디지털통신(Digital Comm.)
5

6. Sampling
|Xs( f )|
Filter property to restore the original
signal from sampled signal
-2fs
-fs
-fm
0
fm
fs
2fs
f
(a)
|Xs( f )|
-2fs
-fs
Sampling theory
0
fs
2fs
fs  2 fm
f
(b)
(a)
디지털통신(Digital Comm.)
f s  2 f m (b)
fs  2 fm
aliasing
6

7. Sampling
 example
 음성신호가 3400Hz의 최대주파수를 가질때 Nyquist 표본화 정리에
의하면 원래의 신호로 완전하게 복원시키려면 최소한 초당 몇번을 표
본화해야 하는가?
f s  2 f max  2  3400  6800 Hz이상
 어떤 신호가 25KHz로 대역제한되어있다. Nyquist 율을 만족하는 최
소표본화주기를 구하라
f s  2 f max  2  25000  50 KHz이상
Ts 
1
1

 20  s
f s 50 KHz
 음성신호를 3KHz로 대역제한해서 Nyquist율로 표본화한 후, 각 표본
을 7bit로 A/D변환하여 전송하려고 할때 전송율은?
2  3000 sample/sec  7  42Kbps
디지털통신(Digital Comm.)
7

8. Sampling methods
~
~
Instantaneous sampling
Ideal sampling
(using impulse train)
F
 Ts (t )  s  s ( )

2 
 s 


Ts 


~
  s ( ) 

 (  k )
s
k  
PAM (t )  T (t )  p(t )
x
s
Realistic sampling
(using rectangular
pulse train)
■ sampling theory
디지털통신(Digital Comm.)
 s   max   max
 s  2 max
8

9. Baseband transmission
x(t )
t
PAM
t
PWM
t
PPM
t
디지털통신(Digital Comm.)
9

10. 펄스진폭 변조(PAM)
자연 표본화
(Natural sampling)
평탄 표본화
(Flat-top sampling)
디지털통신(Digital Comm.)
10

11. 펄스진폭 변조(PAM)
자연 표본화(Natural sampling)
 PAM (t )  x(t ) pTs (t )
p (t )  rect (t  )
  
P( )  sinc

 2 
~
pTs (t )  p(t )   Ts (t )
~
F [ pTs (t )]  F [ p(t )   Ts (t )]
~
 F [ p (t )]F [ Ts (t )]
~
  s P ( )  s ( ).
 
  ssinc
 2
  s
~
  s ( )


 k 
sinc s
 2
k  


 (  k s )



 c  (  k ).
k
s
k  
디지털통신(Digital Comm.)
11

12. 펄스진폭 변조(PAM)

F [ pTs (t )] 
 c  (  k )
k
s
k  
 k  
ck   ssinc s .
 2 
x
*
 PAM (t )  x(t ) pTs (t )


 c  (  k )
k 
k
s
 PAM ( )
 F [ PAM (t )]  F [ x(t ) pTs (t )]

1
F [ x(t )]  F [ pTs (t )]
2


=
=

1
X ( ) 
ck  (  k s )
2
k  



ck
X (  k s ).
2
k  
시간상의 표본화는 주파수상에서
의 주기화를 일으킨다
디지털통신(Digital Comm.)
12

13. Natural sampling
 A 2 kHz sinusoid was sampled at 10 kHz while the sampling pulse duty cycle
was increased from 10% to 50%. The power increases with the duty cycle of the
sampling pulse.
Duty cycle
10%
20%
디지털통신(Digital Comm.)
13

14. Natural sampling
Duty cycle
33%
50%
디지털통신(Digital Comm.)
14

15. Natural sampling
 A 2 kHz sinusoid was sampled with a 25% duty cycle while the sampling
frequency was increased from 10 kHz to 25 kHz. The spectrum indicates that it
would be less difficult to filter out the 2 kHz sinusoid from the samples that are of
higher frequency.
Sampling freq.
10KHz
20KHz
디지털통신(Digital Comm.)
15KHz
25KHz
15

16. Natural sampling
 50% Natural Sampling of a Sinusoid
 This simulation shows time and frequency domain
representations of a naturally sampled sinusoid. To run the
simulation, matlab simulink file : natsamp1.mdl
"Mouse Over" the Spectrum Analyzer or Scope in the Simulink
model to see the output.
디지털통신(Digital Comm.)
16

17. 펄스진폭 변조(PAM)
■ 자연 표본화(natural sampling)에서의 재구성(interpolation)
대역제한 내삽은 ideal
LPF 사용한다 : 구현 불
가능
디지털통신(Digital Comm.)
17

18. Sampling & Reconstruction
 A 2 kHz, 1.5 Vp-p sinusoid was
sampled at 10 kHz with a 33%
duty cycle. The filtered output is
displayed on the bottom trace of
the scope.
Sampling circuit
(a)
디지털통신(Digital Comm.)
18
(c)
(d)

19. 펄스진폭 변조(PAM)
평탄 표본화(flat-top sampling)
PAM (t )  T (t )  p(t )
x
s
~
Ts (t )  x(t )Ts (t ) 
x

 x(kT ) (t  kT )
n  
s
s
 

PAM (t )  Ts (t )  p(t )  p(t )    x(kTs ) (t  kTs )
x

k  


 x(kT )[ p(t )   (t  kT )]   x(kT ) p(t  kT )
n  
디지털통신(Digital Comm.)

s
s
n  
s
s
19

20. 펄스진폭 변조(PAM)
*
=
디지털통신(Digital Comm.)
X
=
20

21. 펄스진폭 변조(PAM)
■ 평탄 표본화(flat-top sampling)에서의 재구성(interpolation)
Equalizer : P(w)의
영향을 보상해주기
위해 사용
 Flat-top sampling된 PAM signal를 복원하기 위해 LPF를 통과시키
면 신호의 왜곡 (signal distortion) 발생
[solution]
 1. sampling pulse duration(τ) << sampling period( Ts )
 2. LPF + equalizer (inverse transfer function of P(w))
equalizer : used to remove the distortion of band-limited pulse
디지털통신(Digital Comm.)
21

22. 펄스진폭 변조(PAM)
표본/유지 회로(Sample & hold circuit)
Flat-top
sampling PAM
modulation
Flat-top
sampling PAM
demodulation
 Sample & hold circuit
 충전과 방전을 이용한 평탄 특성 생성
 Flat-top PAM 신호의 복조(demodulation)에도 이용
디지털통신(Digital Comm.)
22

23. Typical digital communication system
x1
x2
Transmitting
filter
{X k }
x3
channel
T
T
Receiving filter
(equalizing filter)
Detector
ˆ
{X k }
t  kT
noise
(a)
x1
pulse 2
pulse 1
x2
H(f)
{X k }

h(t)
x3
ˆ
{X k}
t  kT
T
T
Detector
noise
(b)
Intersymbol interference in the detection process
(a) Typical baseband digital system (b) Equivalent model
디지털통신(Digital Comm.)
23

24. System transfer function
 Overall equivalent system transfer function
H ( f )  Ht ( f )H c ( f )H r ( f )
H ( f ) represents the composite system transfer function due
to all the filtering at various locations throughout the
transmitter/channel/receiver chain
여기서,
: transmitting filter
Hc ( f )
: filtering within the channel
Hr ( f )
디지털통신(Digital Comm.)
Ht ( f )
: receiving/equalizing filter
24

25. 대역제한(filter)
Causal system → practical band-limited system
W 

W  j 

1



1  ( W ) 2


 ( )   tan 1 ( W )



디지털통신(Digital Comm.)
Non-causal system
-impractical
FT {e  at u (t ), a  0} 
1
a  jw
M ( )  H ( ) 
FT
25

26. ISI (intersymobl interference) & cross talk
Filter
Guard time
디지털통신(Digital Comm.)
26

27. ISI (intersymobl interference) & cross talk
B1, B2, B3 : cutoff-frequency
(a) Pulse train
(b) Interfered by high frequency limit
(c) Interfered by low frequency limit
디지털통신(Digital Comm.)
27

28. 해상도(resolution)
LPF (band-limited
channel) impulse
response
ISI (intersymobl interference)
디지털통신(Digital Comm.)
28

29. 최적의 펄스 형태(optimal pulse shape)
To reduce interference
• increase the channel BW
• band-limit the transmitted pulse BW
→ overlap sync pulses
Sampling time
in receiver
Frequency response of Ideal LPF
디지털통신(Digital Comm.)
29

30. ISI (intersymobl interference)
- Theoretical minimum system bandwidth needed in order to Rs
symbols/s, without ISI
W  1/ 2T  Rs / 2 (Hz)
h (t )
H ( f )
h (t  T )
T

1
2T
0
(a)
1
2T
f
t
0
T
T
(b)
Nyquist channels for zero ISI
(a) Rectangular system transfer function (b) Received pulse shape ht   sinc(t / T )
디지털통신(Digital Comm.)
30

31. ISI (intersymobl interference)
심볼률 패킹 (symbol-rate packing)
: maximum possible symbol transmission rate per hertz
Rs
Rs

2
W Rs / 2
(symbol/s/Hz) : zero ISI
W
※ R
s
: normalized bandwidth (Hz/symbol/s)
Problem)
• Zero ISI only when the sampling is performed at exactly the correct
sampling time
• When tails are large, small timing errors will result in ISI
디지털통신(Digital Comm.)
31

32. ISI (intersymobl interference)
 Pulse shaping to reduce ISI
 올림 코사인 필터 (raised cosine filter)
Commonly used filter of f(t)
이론적인 최소의 대역폭을 초과하는 대역폭 필요
T

T 
 

H ( )   1  sin 
(   W ) 
 2W

2 
0

디지털통신(Digital Comm.)
, 0    (1   )W
, (1   )W    (1   )W
,   (1   )W .
32

33. ISI (intersymobl interference)
상승 코사인(raised cosine) pulse
 sin Wt  cos Wt 
h(t )  

 1  (2Wt  ) 2 

 Wt 

디지털통신(Digital Comm.)
33

34. ISI (intersymobl interference)
- Excess bandwidth : w  W

W
W0  1 / 2T
 W0
: 절대 대역폭
: minimum nyquist bandwidth
- 롤오프 계수 (roll-off factor) :
 
(W  W 0 )  w

W0
W0
measure of the excess
bandwidth of the filter
 0
: case of minimum nyquist bandwidth
 1
: excess bandwidth = 100%
1 symbol/s/Hz의 심볼률 패킹을 얻음
-일반적인 관계
1
W  (1   ) Rs
2
; Baseband transmission
W  (1   ) Rs
;Bandpass transmission
디지털통신(Digital Comm.)
34

35. 예) Digital Satellite Receiver


Fully DVB-S/MPEG-2 Compliant
• Highly Sensitive, Low Eb/No Tuner (920-2150MHz)
• QPSK Demodulator with Symbol Rate 2-50MS/s,SCPC and MCPC Compatible
• 10 Level LED Signal Strength Indicator
• Memory Space Capable of 1200 Channels
• Max.16 Satellite Input Support
• Automatic NTSC/PAL Detection
• Auto Searching Satellite Programs
• Auto Memorization of Frequency Deviation for Fast Program Searching
• Manual Edit Video, Audio, TTX and PCR PIDs etc
• Favorite Channels Support
• Parental Lock Function
• RF Modulator(CH 21-69)
• 32 Step Volume Control
• Compatible with CCIR/ITU-R Broadcast
• DiSEqC 1.0 LNB Control Protocol Support
• 0/12V, 13/18V, 22KHz for LNB Switching
• Software Upgradable Via RS-232
• Mechanical Polarizer Control(+5V Pulse GND)
GENERAL
- Colour OSD, Easy-to-Use Menu
- Operating Temp. -5° C to+50°C
- Power Supply Voltage...85 to 265V AC50/60Hz
- Main Power ON/OFF Switch
- Power Consumption Max, 30W .(Stand by 5W)
- Weight Approx. 2.8Kg
DEMODULATOR
http://www.digicomcatv.com/dsreceiver.php

-
Waveform QPSK
Symbol Rate 2-50MS/s
Roll off Factor 0.35
Outer Decoder Reed-Solomon (204,188,8)
Code Rate 1/2, 2/3, 3/4, 5/6, 7/8
SCPC and MCPC Compatible
Audio Decoder MPEG-1 Layer I and II
Audio Channel Mono, Dual Channels, Stereo
Volume Control 32 Steps Adjustable.
디지털통신(Digital Comm.)
35

36. Eye pattern
 아이 패턴 (eye pattern)
기저대역 신호에 대한 시스템의 응답을 측정하여 오실로스코프로 표
시
 최적의 표본화 시간은 최대의 눈 개방(eye opening)에 상응하며 잡음
으로부터 신호를 최대한 보호
 심볼 간 간섭이 증가할 수록 눈이 감겨지고, 심볼 간 간섭이 감소할 수
록 눈이 떠짐
송신부
디지털통신(Digital Comm.)
수신부
36

37. Eye pattern
최적 표본화 시간
시간 오류에
대한 민감도
심볼 간 간섭에
의한 왜곡
시간 지터
(timing jitter)의
측정값
잡음 마진
(noise margin)
심볼 간 간섭에 의한 아이 패턴
디지털통신(Digital Comm.)
37

38. PAM, PWM, PPM


 t  nTs 
[ x(nTs )  C ]rect

 PAM (t ) 
  
n  


, C  x(t ) max




 t  nTs 
rect

 PWM (t ) 
  
n  


,   kW x(nTs )  C


, kW x(t ) max  C  Ts  kW x(t ) max .





 t  nTs  a 
rect

 PPM (t ) 



n  


, a  k P x(nTs )  C


, k P x(t ) max  C  Ts    k P x(t ) max .





디지털통신(Digital Comm.)
38

39. PAM, PWM, PPM
디지털통신(Digital Comm.)
39