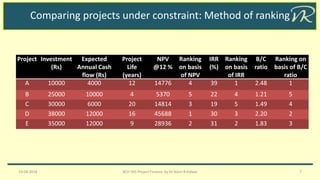
The document discusses the evaluation of investment projects under capital constraints, emphasizing the impact of project dependency and capital rationing on decision-making. It outlines different types of project relationships (independent, mutually exclusive, negatively dependent, and positively dependent) and presents methods for comparing projects, including ranking approaches and mathematical programming models. The analysis highlights how conflicts can arise in project ranking due to size, time, and life disparities, and suggests approaches to resolve these issues.

1. Multiple Projects and
Constraints
19-04-2018 BCH 505 Project Finance by Dr Naim R Kidwai 1

2. Multiple projects and constraints
• In isolation, Investment projects can be evaluated on any of discounted
cash flow method (NPV, IRR, B/C ratio etc.) for correct decision making.
• In existing organization capital investment decisions can’t be taken in
isolation due to lack of capital rationing and project independence
• Without considering the constraints, the rational criterion of project
evaluation (NPV, IRR, etc) may lead to wrong decisions
19-04-2018 BCH 505 Project Finance by Dr Naim R Kidwai 2

3. Constraints: Project dependence
Project A and B are financially independent if acceptance or rejection of one does not
affect the cash flow of other or does not affect acceptance or rejection of other. (Ex.
Investment in boiler and investment in computer network are independent)
Mutually exclusive projects: (Alternative projects) . Acceptance of one project
automatically precludes the other mutually exclusive projects.
Negatively dependent projects : Projects though not mutually exclusive but negatively
influence each others cash flows (Ex. Building a bridge and buying commercial ferry)
Positively dependent projects: (Complementary projects) undertaking of a project
positively affects cash flows of other.
▪ symmetric complementary: positive effect in both direction only (taking A or B
benefits other)
▪ asymmetric complementary: positive effect in one direction only (taking A benefits B
but taking B does not benefit A)
19-04-2018 BCH 505 Project Finance by Dr Naim R Kidwai 3

4. Constraints: Capital Rationing
• Capital rationing exists when capital available is
inadequate to undertake all projects which are
otherwise acceptable.
• Capital rationing may arise because of internal
limitation or external constraints.
• Internal capital rationing is caused by management
decision to set a limit on capital expenditure outlays.
• External capital rationing arise out of firm’s inability to
raise sufficient fund at a given cost of capital.
• Implication of cost of capital curve is that some projects
which might have been acceptable if cost of capital
being constant , have to be abandoned or postponed
19-04-2018 BCH 505 Project Finance by Dr Naim R Kidwai 4
Quantum of fund raised
Costofcapital

5. Constraints:
Project Indivisibility: A Capital project has to be accepted in Toto i.e. it can not be
accepted partially
Ex. Three indivisible projects A, B and C require investment of Rs 5 crore, 4 crore and 3
crore. NPV of the projects are 2 crore, 1.5 crore and 1 crore respectively.
On the basis of NPV Project A is superior. But acceptance of A with NPV of 2 crore
makes sure rejection of B and C due to capital rationing, which together provides NPV
of 2.5 crore.
Thus comparison of projects under constraints is required to make a suitable financial
decision
19-04-2018 BCH 505 Project Finance by Dr Naim R Kidwai 5

6. Comparing projects under constraint: Method of ranking
Approaches of comparing projects under constraints
▪ Method of ranking
▪ Method of mathematical Programming
Method of ranking consists of two steps
o Rank all project under descending order on the basis of financial criterion ( NPV,
etc.)
o Accept project in same order till the capital is exhausted
Method of ranking is impaired with two problems
• Conflict in ranking as per discounted cash flow criteria
• Project indivisibility
19-04-2018 BCH 505 Project Finance by Dr Naim R Kidwai 6

7. Comparing projects under constraint: Method of ranking
Project Investment
(Rs)
Expected
Annual Cash
flow (Rs)
Project
Life
(years)
NPV
@12 %
Ranking
on basis
of NPV
IRR
(%)
Ranking
on basis
of IRR
B/C
ratio
Ranking on
basis of B/C
ratio
A 10000 4000 12 14776 4 39 1 2.48 1
B 25000 10000 4 5370 5 22 4 1.21 5
C 30000 6000 20 14814 3 19 5 1.49 4
D 38000 12000 16 45688 1 30 3 2.20 2
E 35000 12000 9 28936 2 31 2 1.83 3
19-04-2018 BCH 505 Project Finance by Dr Naim R Kidwai 7

8. Comparing projects under constraint: Ranking Conflicts
In a given set of Projects, preference ranking tends to differ from one criterion to
other criterion
Conflicts in project ranking may arise because of
▪ size disparity: Size of the capital projects may tremendously differ ( NPV refers to
size while IRR and B/C ratio does not refers to size of capital)
▪ Time disparity: due to varying pattern of cash inflows ( IRR assumes that cash
inflows can be reinvested at the same rate or return while NPV and B/C ratio
analysis assumes that cash inflows can be reinvested at the firms cost of capital).
It may be solved by defining reinvestment rate.
▪ Life disparity: When mutually exclusive alternatives have different project life. This
conflict can be taken care by defining reinvestment rate.
19-04-2018 BCH 505 Project Finance by Dr Naim R Kidwai 8

9. Comparing projects under constraint: Project Indivisibility
Project indivisibility may pose a problem in project ranking method.
The problem may be resolved by Feasible combination approach
• Defined all possible combinations considering the constraints
• Choose the feasible combination which has large NPV
19-04-2018 BCH 505 Project Finance by Dr Naim R Kidwai 9

10. Comparing projects under constraint:
Mathematical programming approach
Feasible combination approach tends to be cumbersome if number of projects
increases.
The solution lies in mathematical programming model. This approach helps in
determining optimum solution ( most desirable combination of projects)
A mathematical model is formulated in form of
• Objective function
• Constraint equation
Type of mathematical programming models
• Linear Programming model
• Integer Programming model
• Goal Programming Model
19-04-2018 BCH 505 Project Finance by Dr Naim R Kidwai 10

11. Thank You
19-04-2018 BCH 505 Project Finance by Dr Naim R Kidwai 11
Contact
Email: naimkidwai@gmail.com
https://nrkidwai.wordpress.com/