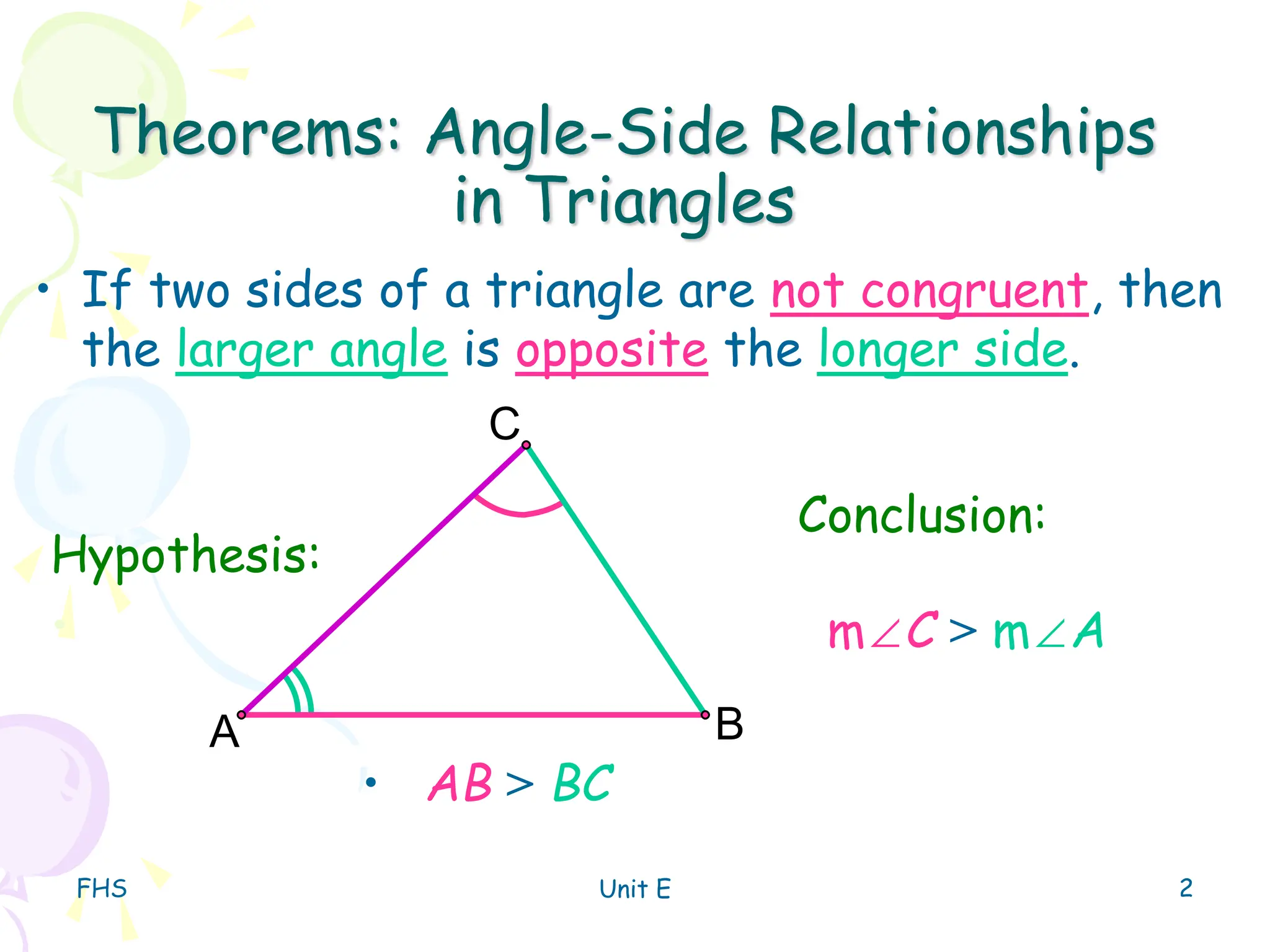
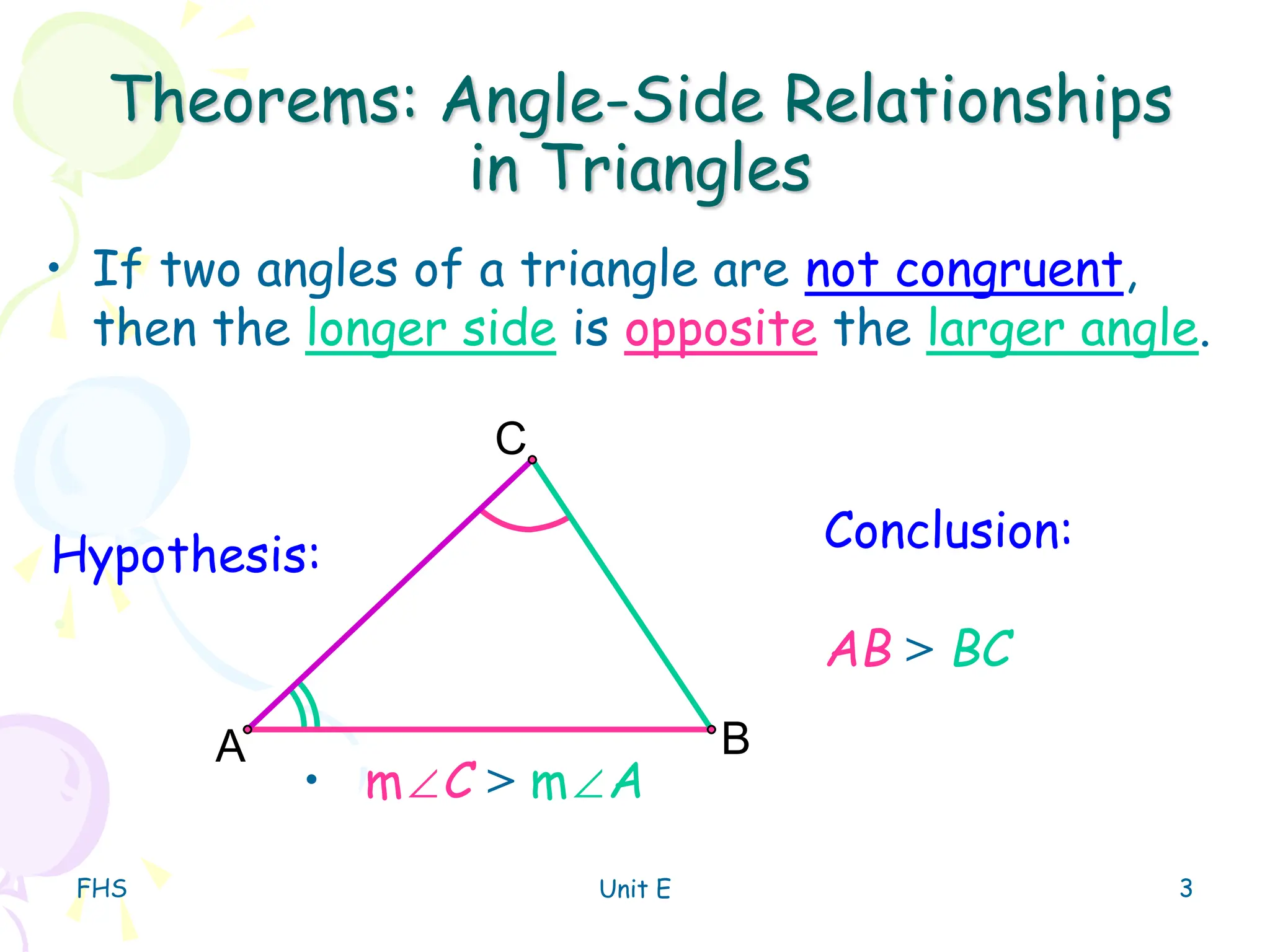
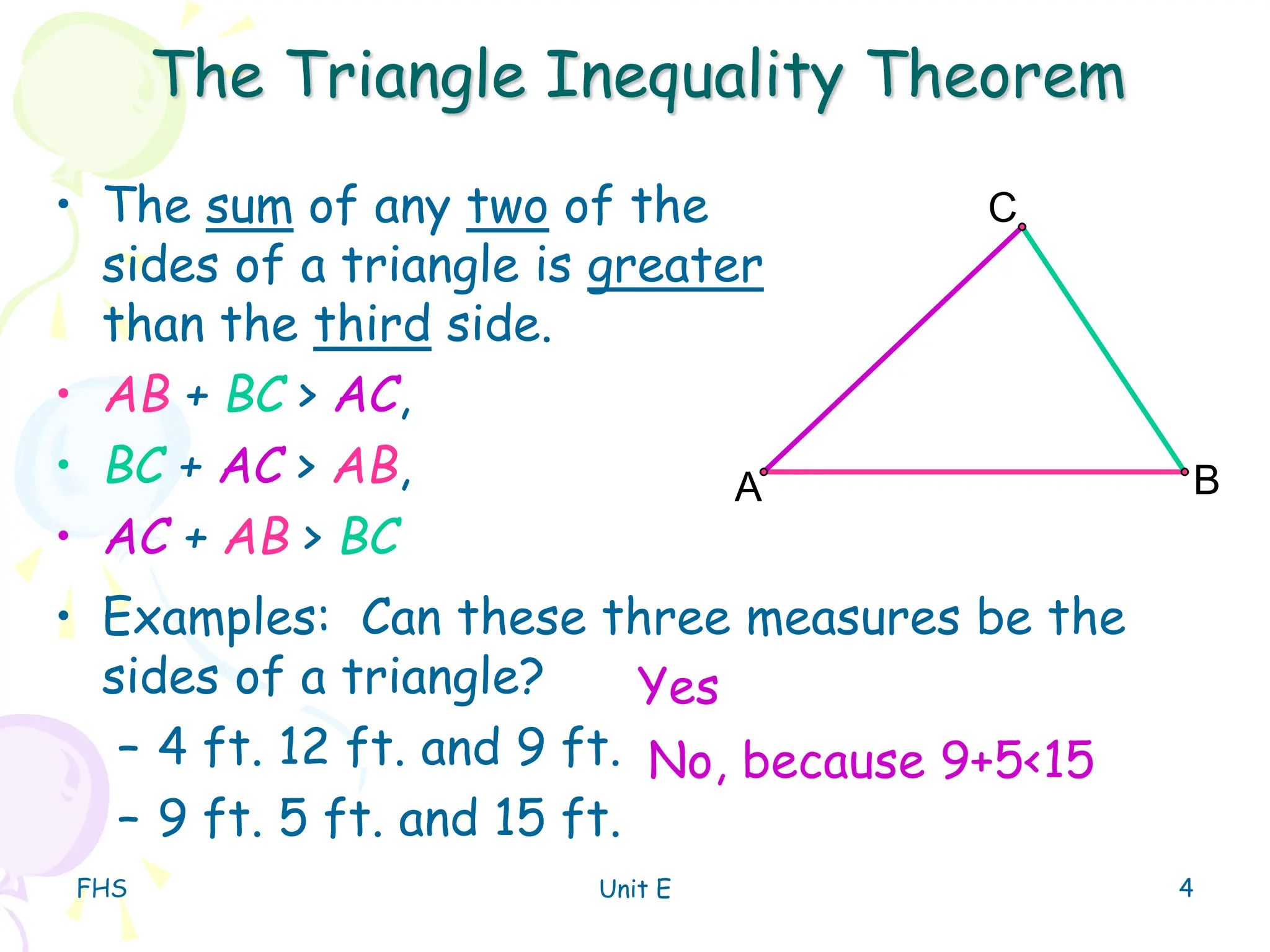
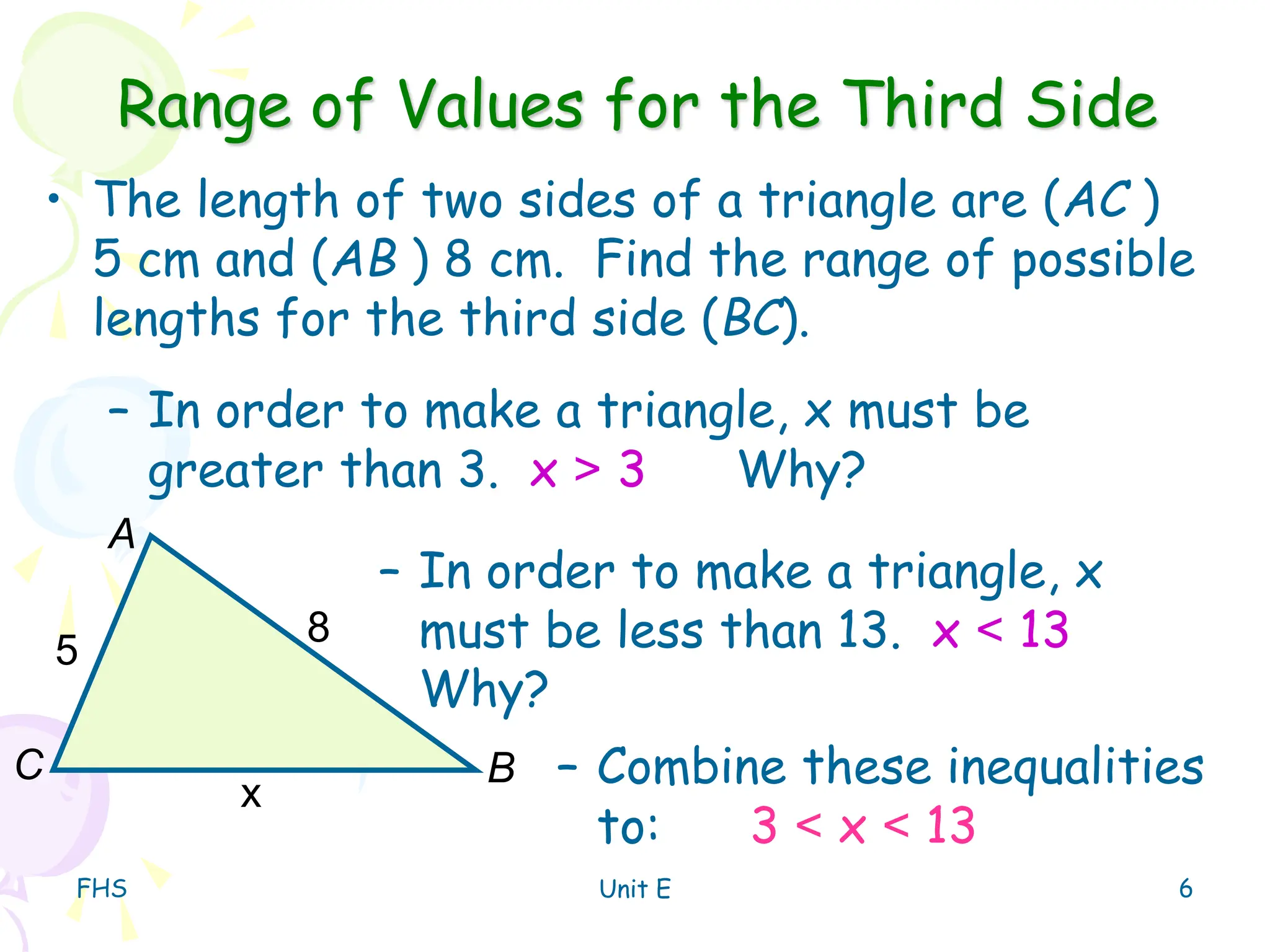The document discusses the triangle inequality theorem, which states that the sum of any two side lengths of a triangle must be greater than the third side length. It provides examples of determining whether a triangle can exist given three side lengths, and how to find the range of possible lengths for the third side of a triangle given the lengths of two sides.

1. Triangle Inequality
Theorem
Students will be able to apply the triangle
inequality theorem to find missing angles.
T.2.G.2: Investigate the measures of segments to
determine the existence of triangles (triangle
inequality theorem)

2. FHS Unit E 2
Theorems: Angle-Side Relationships
in Triangles
• If two sides of a triangle are not congruent, then
the larger angle is opposite the longer side.
A B
C
Conclusion:
m∠C > m∠A
• AB > BC
Hypothesis:
•

3. FHS Unit E 3
Theorems: Angle-Side Relationships
in Triangles
• If two angles of a triangle are not congruent,
then the longer side is opposite the larger angle.
A B
C
• m∠C > m∠A
Conclusion:
AB > BC
Hypothesis:
•

4. FHS Unit E 4
• Examples: Can these three measures be the
sides of a triangle?
– 4 ft. 12 ft. and 9 ft.
– 9 ft. 5 ft. and 15 ft.
The Triangle Inequality Theorem
• The sum of any two of the
sides of a triangle is greater
than the third side.
• AB + BC > AC,
• BC + AC > AB,
• AC + AB > BC
A B
C
Yes
No, because 9+5<15

5. FHS Unit E 5
Shortcut to Using Triangle
Inequality Theorem
Tell whether a triangle can have sides with
the lengths of 8, 13, and 21. Explain.
No.
We need to test these numbers using the Triangle
Inequality Theorem, Add the smallest two
numbers together and see if the sum is larger
than the third number.
If the sum is larger, then they can make a triangle.
If the sum is not larger, then they cannot make a
triangle.

6. FHS Unit E 6
Range of Values for the Third Side
• The length of two sides of a triangle are (AC )
5 cm and (AB ) 8 cm. Find the range of possible
lengths for the third side (BC).
– In order to make a triangle, x must be
greater than 3. x > 3 Why?
A
C B
5
8
x
– In order to make a triangle, x
must be less than 13. x < 13
Why?
– Combine these inequalities
to: 3 < x < 13

7. FHS Unit E 7
• In other words, this is what we do to get
to the answer.
– Subtract the two given sides: 8 – 5 = 3
– Add the two given sides: 8 + 5 = 13
A
C B
5 8
– Plug these two numbers into
the inequality:
3 < x < 13
x
Range of Values for the Third Side

8. FHS Unit E 8
1. Write the angles in order from smallest to
largest.
2. Write the sides in order from shortest to
longest.
Lesson Quiz: Part I
C, B, A
, ,
DE EF DF

9. FHS Unit E 9
Lesson Quiz: Part II
3. The lengths of two sides of a triangle are 17 cm and
12 cm. Find the range of possible lengths for the
third side.
4. Tell whether a triangle can have sides with lengths
2.7, 3.5, and 9.8. Explain.
No; 2.7 + 3.5 > 9.8.
5 cm < x < 29 cm
Yes; the sum of any two lengths is
greater than the third length.
5. Ray wants to place a chair so it is 10
ft from his television set. Can the
other two distances shown be 8 ft
and 6 ft? Explain.