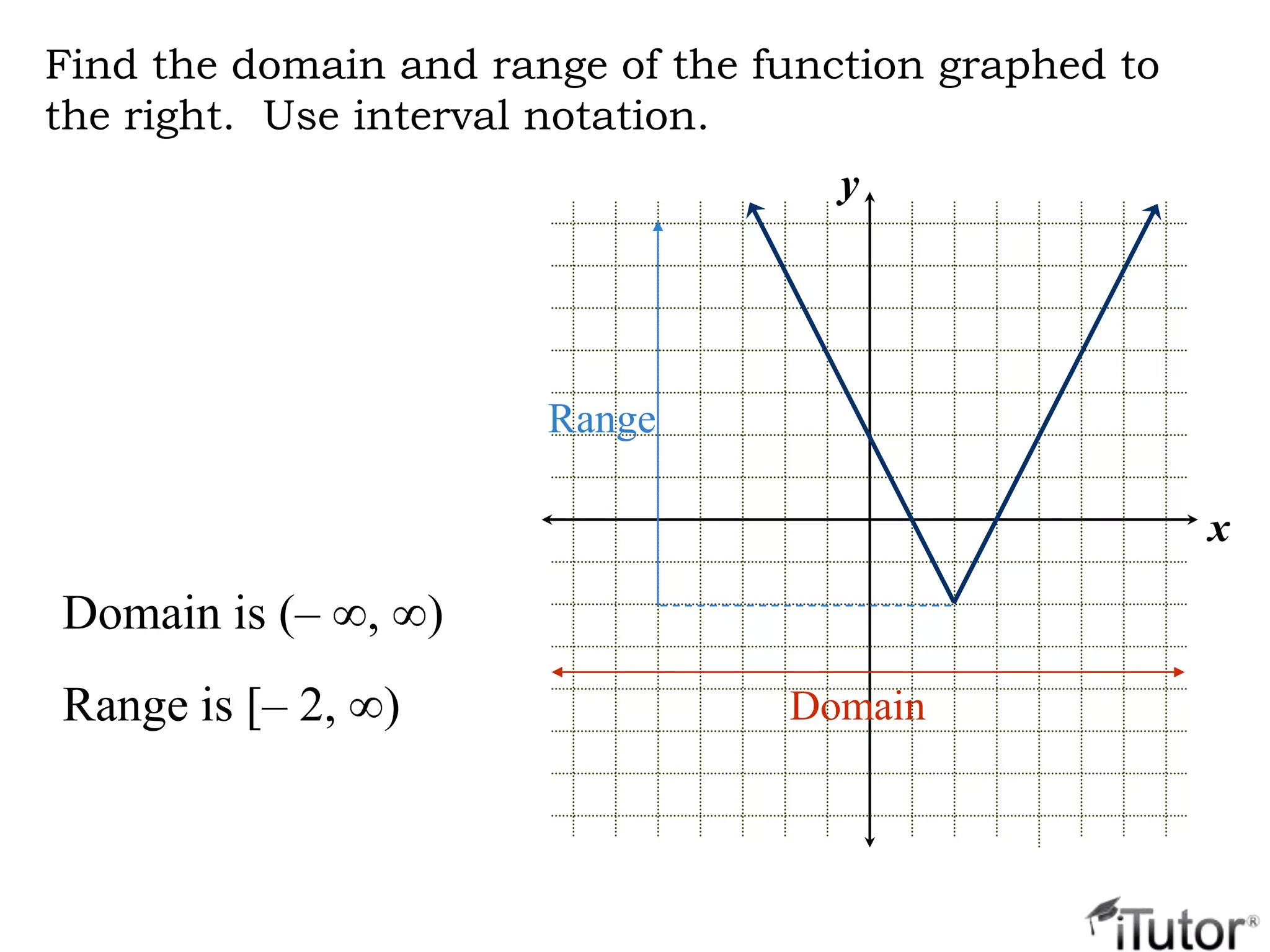
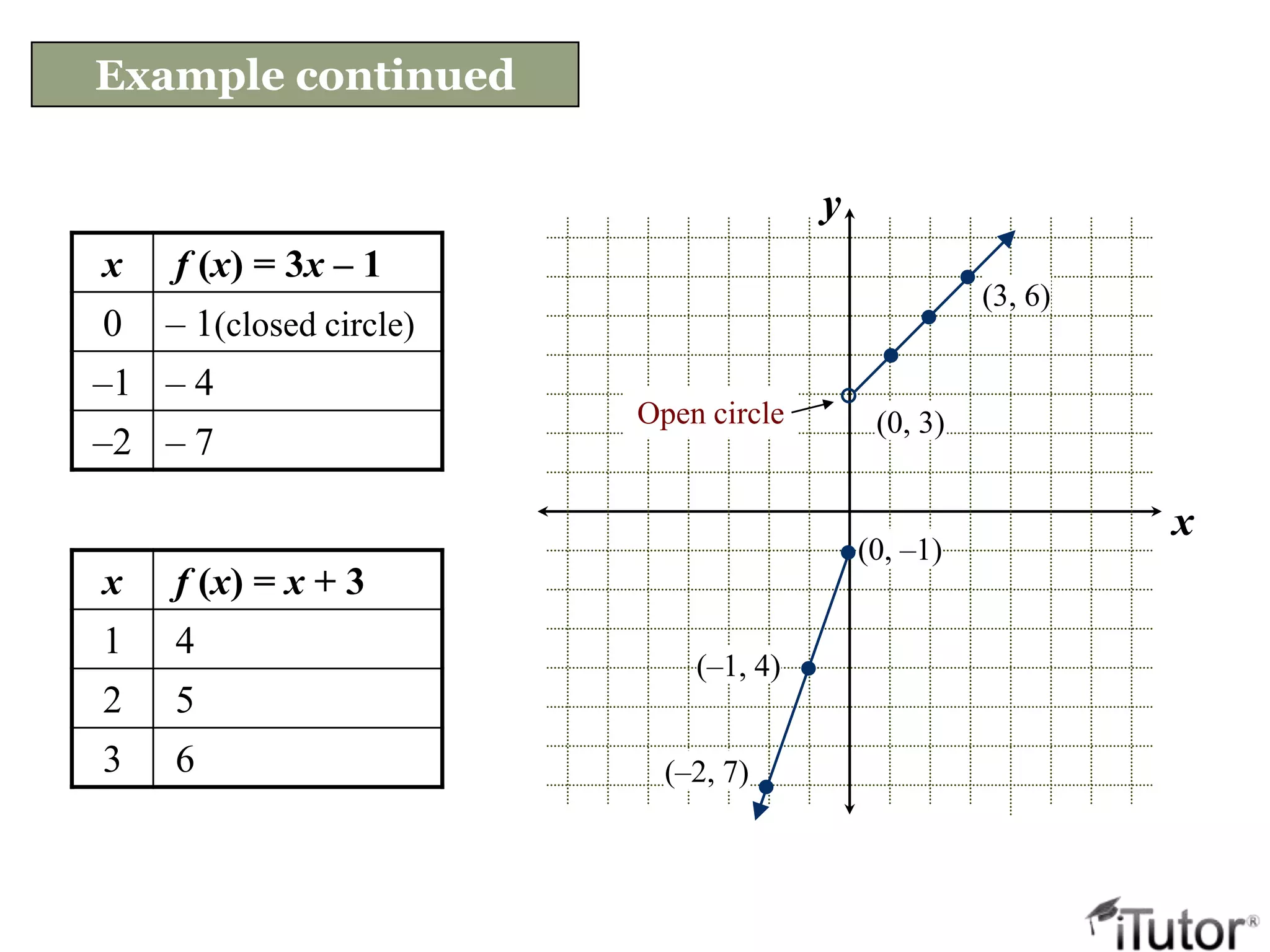
This document introduces methods for solving quadratic equations beyond factoring, including the square root property, completing the square, and the quadratic formula. It discusses how to determine the number and type of solutions based on the discriminant. The key steps are presented for solving quadratics, graphing quadratic functions as parabolas, and finding the domain and range. Piecewise-defined quadratic functions are also explained.

1. Martin-Gay, Developmental Mathematics 1
T- 1-855-694-8886
Email- info@iTutor.com
By iTutor.com

2. Solving Quadratic Equation by Square Root Property
 We previously have used factoring to solve quadratic equations.
 This chapter will introduce additional methods for solving
quadratic equations.
 Square Root Property
 If b is a real number and a2 = b, then ba
Example
♦ Solve x2 = 49
2x
♦ Solve (y – 3)2 = 4
♦ Solve 2x2 = 4
x2 = 2
749x
y = 3 2
y = 1 or 5
243y
♦ Solve x2 + 4 = 0
x2 = 4
There is no real solution
because the square root of 4
is not a real number.

3. Solve (x + 2)2 = 25
x = 2 5
x = 2 + 5 or x = 2 – 5
x = 3 or x = 7
5252x
Example
Solve (3x – 17)2 = 28
72173x
3
7217
x
72283x – 17 =

4. In all four of the previous examples, the constant in the square
on the right side, is half the coefficient of the x term on the left.
Also, the constant on the left is the square of the constant on the
right.
So, to find the constant term of a perfect square trinomial, we
need to take the square of half the coefficient of the x term in the
trinomial (as long as the coefficient of the x2 term is 1, as in our
previous examples).
Solving quadratic Equation by Completing the Square
Example
What constant term should be added to the following expressions
to create a perfect square trinomial?
x2 – 10x
add 52 = 25
x2 + 16x
add 82 = 64
x2 – 7x
add
4
49
2
7
2

5. We now look at a method for solving quadratics that involves a
technique called completing the square.
It involves creating a trinomial that is a perfect square, setting
the factored trinomial equal to a constant, then using the square
root property from the previous section.
Example
Solving a Quadratic Equation by Completing a Square
1) If the coefficient of x2 is NOT 1, divide both sides of the
equation by the coefficient.
2) Isolate all variable terms on one side of the equation.
3) Complete the square (half the coefficient of the x term squared,
added to both sides of the equation).
4) Factor the resulting trinomial.
5) Use the square root property.

6. Solve by completing the square. y2 + 6y = 8
y2 + 6y + 9 = 8 + 9
(y + 3)2 = 1
y = 3 1
y = 4 or 2
y + 3 = = 11
Example
Solve by completing the square. y2 + y – 7 = 0
y2 + y = 7
y2 + y + ¼ = 7 + ¼
2
29
4
29
2
1
y
2
291
2
29
2
1
y
(y + ½)2 = 4
29

7. The Quadratic Formula
♦ Another technique for solving quadratic equations is to use the
quadratic formula.
♦ The formula is derived from completing the square of a general
quadratic equation.
♦ A quadratic equation written in standard form, ax2 + bx + c = 0,
has the solutions.
a
acbb
x
2
42
Example
♦ Solve 11n2 – 9n = 1 by the quadratic formula.
11n2 – 9n – 1 = 0, so
a = 11, b = -9, c = -1
)11(2
)1)(11(4)9(9 2
n
22
44819
22
1259
22
559

8. The Discriminant
♦The expression under the radical sign in the formula (b2 – 4ac) is
called the discriminant.
♦The discriminant will take on a value that is positive, 0, or negative.
♦The value of the discriminant indicates two distinct real solutions,
one real solution, or no real solutions, respectively.
Example
Use the discriminant to determine the number and type of
solutions for the following equation.
5 – 4x + 12x2 = 0
a = 12, b = –4, and c = 5
b2 – 4ac = (–4)2 – 4(12)(5)
= 16 – 240
= –224
There are no real solutions.

9. Steps in Solving Quadratic Equations
1. If the equation is in the form (ax + b)2 = c, use the square
root property to solve.
2. If not solved in step 1, write the equation in standard form.
3. Try to solve by factoring.
4. If you haven’t solved it yet, use the quadratic formula.
Example
♦ Solve 12x = 4x2 + 4.
0 = 4x2 – 12x + 4
0 = 4(x2 – 3x + 1)
Let a = 1, b = -3, c = 1
)1(2
)1)(1(4)3(3 2
x
2
493
2
53
0
2
1
8
5 2
mm
0485 2
mm
0)2)(25( mm
02025 mm or
2
5
2
mm or
♦ Solve the following

10. x
y
Graph y = 2x2 – 4.
x y
0 –4
1 –2
–1 –2
2 4
–2 4
(2, 4)(–2, 4)
(1, –2)(–1, – 2)
(0, –4)
Graphs of Quadratic Equations
Example
♦The graph of a quadratic equation is a parabola.
♦The highest point or lowest point on the parabola is the vertex.

11. Although we can simply plot points, it is helpful to know
some information about the parabola we will be graphing prior to
finding individual points.
To find x-intercepts of the parabola, let y = 0 and solve for x.
To find y-intercepts of the parabola, let x = 0 and solve for y.
Intercepts of the Parabola
Characteristics of the Parabola
♦ If the quadratic equation is written in standard form,
y = ax2 + bx + c,
1) the parabola opens up when a > 0 and opens down when a < 0.
2) the x-coordinate of the vertex is .
a
b
2
To find the corresponding y-coordinate, you substitute the x-coordinate
into the equation and evaluate for y.

12. x
y
Graph y = –2x2 + 4x + 5.
x y
1 7
2 5
0 5
3 –1
–1 –1
(3, –1)(–1, –1)
(2, 5)(0, 5)
(1, 7)
Since a = –2 and b = 4, the
graph opens down and the x-
coordinate of the vertex is
1
)2(2
4
Example

13. Domain and Range
Recall that a set of ordered pairs is also called a relation.
The domain is the set of x-coordinates of the ordered pairs.
The range is the set of y-coordinates of the ordered pairs.
Example
Find the domain and range of the relation
{(4,9), (–4,9), (2,3), (10, –5)}
♦ Domain is the set of all x-values, {4, –4, 2, 10}
♦ Range is the set of all y-values, {9, 3, –5}

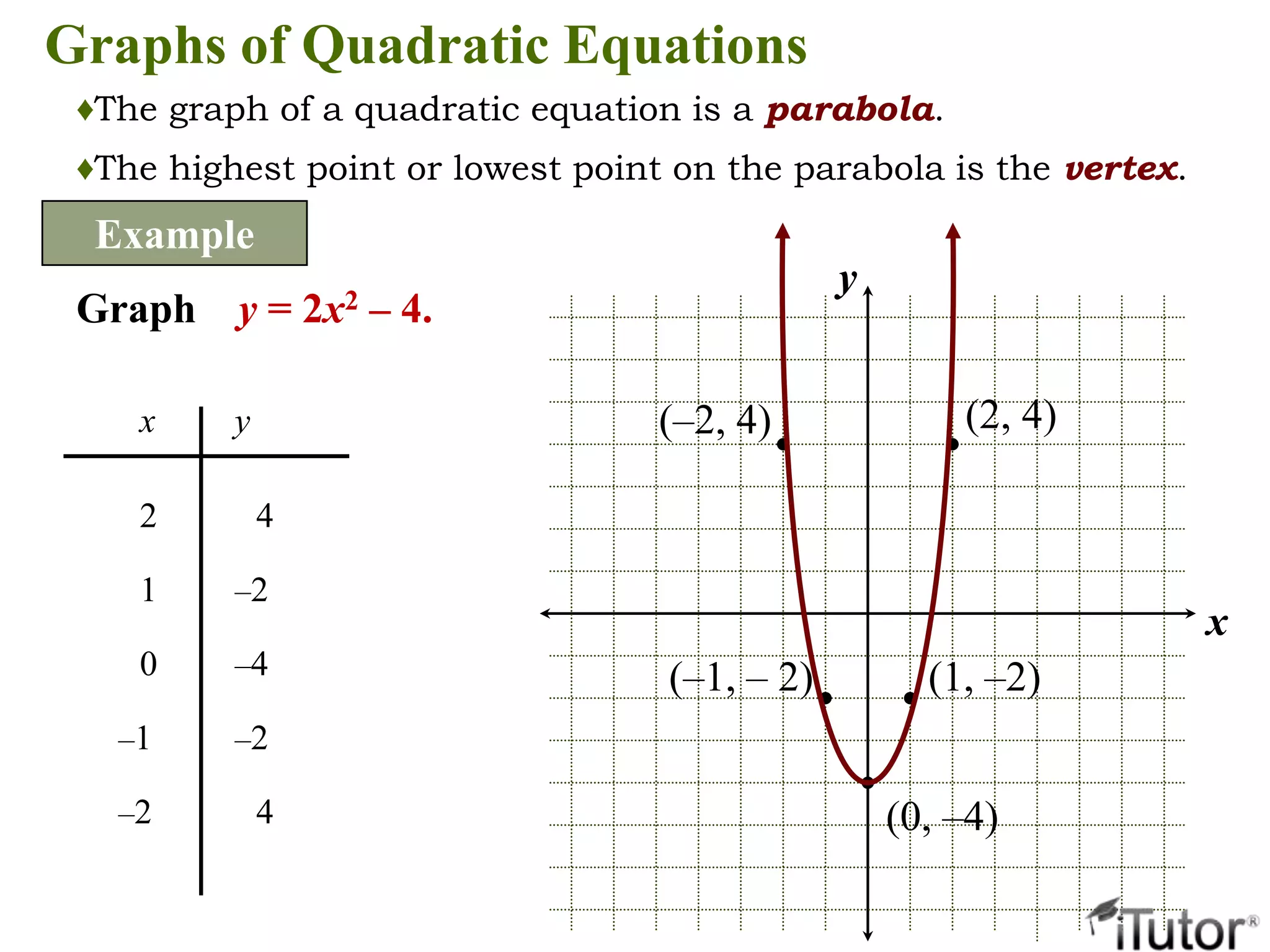
14. Find the domain and range of the function graphed to the
right. Use interval notation.
x
y
Domain is [–3, 4]
Domain
Range is [–4, 2]
Range
Example

15. Find the domain and range of the function graphed to
the right. Use interval notation.
x
y
Domain is (– , )
DomainRange is [– 2, )
Range

16. Graph each “piece” separately.
Graph
3 2 if 0
( ) .
3 if 0
x x
f x
x x
Graphing Piecewise-Defined Functions
Example
Continued.
x f (x) = 3x – 1
0 – 1(closed circle)
–1 – 4
–2 – 7
x f (x) = x + 3
1 4
2 5
3 6
Values 0. Values > 0.

17. Example continued
x
y
x f (x) = x + 3
1 4
2 5
3 6
x f (x) = 3x – 1
0 – 1(closed circle)
–1 – 4
–2 – 7
(0, –1)
(–1, 4)
(–2, 7)
Open circle (0, 3)
(3, 6)

18. Martin-Gay, Developmental Mathematics 18
The End
Call us for more
information:
www.iTutor.com
1-855-694-8886
Visit