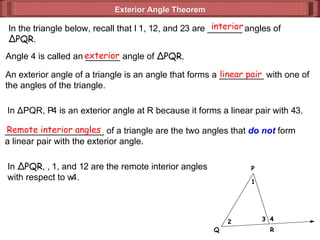
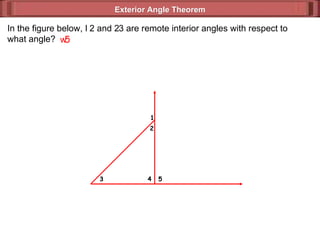
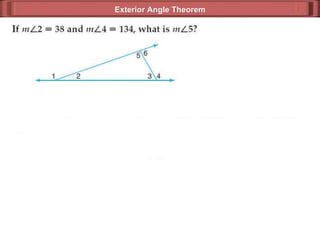
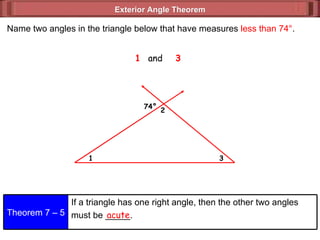
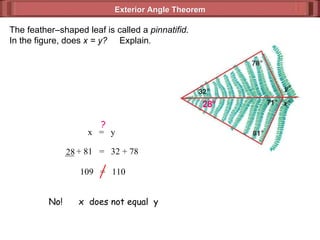
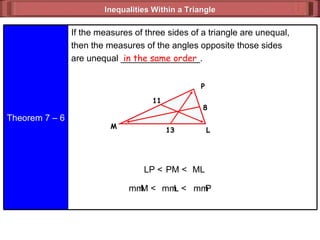
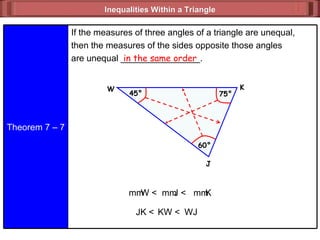
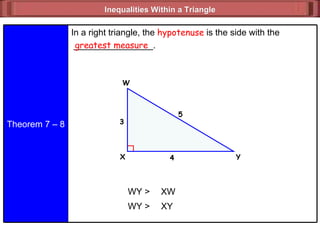
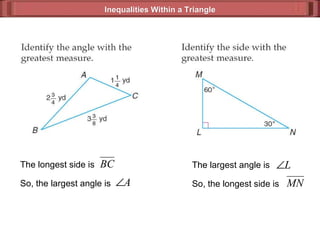
The document discusses various theorems and properties related to triangles, including: 1) The exterior angle theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of its two remote interior angles. 2) The triangle inequality theorem states that the sum of the measures of any two sides of a triangle is greater than the measure of the third side. 3) Properties relating the lengths of sides and measures of angles in a triangle, such as if sides are unequal then angles will be unequal as well.

1. Triangle Inequalities § 7.1 Segments, Angles, and Inequalities § 7.4 Triangle Inequality Theorem § 7.3 Inequalities Within a Triangle § 7.2 Exterior Angle Theorem

2. Segments, Angles, and Inequalities For any numbers a, b, and c, 1) if a < b and b < c, then a < c. 2) if a > b and b > c, then a > c. if 5 < 8 and 8 < 9, then 5 < 9. if 7 > 6 and 6 > 3, then 7 > 3. Property Transitive Property

3. Segments, Angles, and Inequalities For any numbers a, b, and c, For any numbers a, b, and c, 1) if a < b, then a + c < b + c and a – c < b – c. 2) if a > b, then a + c > b + c and a – c > b – c. 1 < 3 1 + 5 < 3 + 5 6 < 8 Property Addition and Subtraction Properties Multiplication and Division Properties

4. Exterior Angle Theorem You will learn to identify exterior angles and remote interior angles of a triangle and use the Exterior Angle Theorem . What You'll Learn 1) Interior angle 2) Exterior angle 3) Remote interior angle Vocabulary

5. Exterior Angle Theorem In the triangle below, recall that  1,  2, and  3 are _______ angles of Δ PQR. interior Angle 4 is called an _______ angle of Δ PQR. exterior An exterior angle of a triangle is an angle that forms a _________ with one of the angles of the triangle. linear pair In Δ PQR,  4 is an exterior angle at R because it forms a linear pair with  3. ____________________ of a triangle are the two angles that do not form a linear pair with the exterior angle. Remote interior angles In Δ PQR ,  1, and  2 are the remote interior angles with respect to  4. 1 2 3 4 P Q R

6. Exterior Angle Theorem In the figure below,  2 and  3 are remote interior angles with respect to what angle?  5 1 2 3 4 5

7. Exterior Angle Theorem remote interior angles m  4 = m  1 + m  2 Theorem 7 – 3 Exterior Angle Theorem The measure of an exterior angle of a triangle is equal to sum of the measures of its ___________________. X 4 3 2 1 Z Y

8. Exterior Angle Theorem

9. Exterior Angle Theorem remote interior angles m  4 > m  1 m  4 > m  2 Theorem 7 – 4 Exterior Angle Inequality Theorem The measure of an exterior angle of a triangle is greater than the measures of either of its two ____________________. X 4 3 2 1 Z Y

10. Exterior Angle Theorem  1 and  3 Name two angles in the triangle below that have measures less than 74 ° . acute 74° 1 3 2 Theorem 7 – 5 If a triangle has one right angle, then the other two angles must be _____.

11. Exterior Angle Theorem

12. Exterior Angle Theorem The feather–shaped leaf is called a pinnatifid. In the figure, does x = y? Explain . __ + 81 = 32 + 78 28 28 ° 109 = 110 No! x does not equal y x = y ?

13. Inequalities Within a Triangle You will learn to identify the relationships between the _____ and _____ of a triangle. What You'll Learn sides angles Nothing New! Vocabulary

14. Inequalities Within a Triangle in the same order LP < PM < ML m  M < m  P m  L < Theorem 7 – 6 If the measures of three sides of a triangle are unequal, then the measures of the angles opposite those sides are unequal ________________. 13 8 11 L P M

15. Inequalities Within a Triangle in the same order JK < KW < WJ m  W < m  K m  J < Theorem 7 – 7 If the measures of three angles of a triangle are unequal, then the measures of the sides opposite those angles are unequal ________________. J 45° W K 60° 75°

16. Inequalities Within a Triangle greatest measure WY > XW 3 5 4 WY > XY Theorem 7 – 8 In a right triangle, the hypotenuse is the side with the ________________. Y W X

17. Inequalities Within a Triangle The longest side is So, the largest angle is The largest angle is So, the longest side is

18. Triangle Inequality Theorem You will learn to identify and use the Triangle Inequality Theorem . What You'll Learn Nothing New! Vocabulary

19. Triangle Inequality Theorem greater a + b > c a + c > b b + c > a Theorem 7 – 9 Triangle Inequality Theorem The sum of the measures of any two sides of a triangle is _______ than the measure of the third side. a b c

20. Triangle Inequality Theorem Can 16, 10, and 5 be the measures of the sides of a triangle? No! 16 + 10 > 5 16 + 5 > 10 However, 10 + 5 > 16