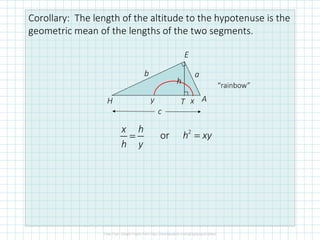
Similar right triangles have the following properties: 1) The lengths of corresponding sides are proportional and angles are equal. 2) The altitude to the hypotenuse divides the triangle into two smaller right triangles that are similar to the original triangle. 3) The length of the altitude to the hypotenuse is the geometric mean of the lengths of the two segments of the hypotenuse.

1. Similar Right Triangles
The student is able to (I can):
• Use the geometric mean to find segment lengths in right
triangles
• Apply similarity relationships in right triangles to solve
problems.

2. geometricgeometricgeometricgeometric meanmeanmeanmean – a proportion with the following pattern:
or
which end up as
Example: Find the geometric mean of 5 and 20.
a x
x b
= 2
x ab=
x ab=
5
20
x
x
=
2
100x =
x = 10

3. Theorem: The altitude to the hypotenuse of a right triangle
forms two triangles that are similar to each other and to the
original triangle.
T
I
ME
I T
M
E
I
T
IE
M
90˚−∠M
90˚−∠M
ΔMIT ~ ΔIET ~ ΔMEI

4. Because the triangles are similar, we can set up proportions
between the sides:
T
I
ME
I T
M
E
I
T
IE
M
ΔMIT ~ ΔIET ~ ΔMEI
, etc.
MI IE ME
IT ET EI
= =

5. Corollary: The length of the altitude to the hypotenuse is the
geometric mean of the lengths of the two segments.
H
E
AT
ab
xy
c
x h
h y
= or 2
h xy=
h “rainbow”

6. Corollary: The length of a leg of a right triangle is the
geometric mean of the lengths of the hypotenuse and the
segment of the hypotenuse adjacent to that leg.
H
E
AT
ab
xy
c
h
x a
a c
= or 2
a xc=
y b
b c
= or 2
b yc=
“horns”

7. Example: Find x, y, and z.
9 6
x
y
z
9 6
6
9 36
4
x
x
x
=
=
=
2
9
9 4
117
3 13
z
z
z
z
=
+
=
=
2
4
9 4
52
2 13
y
y
y
y
=
+
=
=
or use Pyth.
Theorem to
find y and z.
2 2 2
2
9 6
117
3 13
z
z
z
= +
=
=
2 2 2
2
4 6
52
2 13
y
y
y
= +
=
=