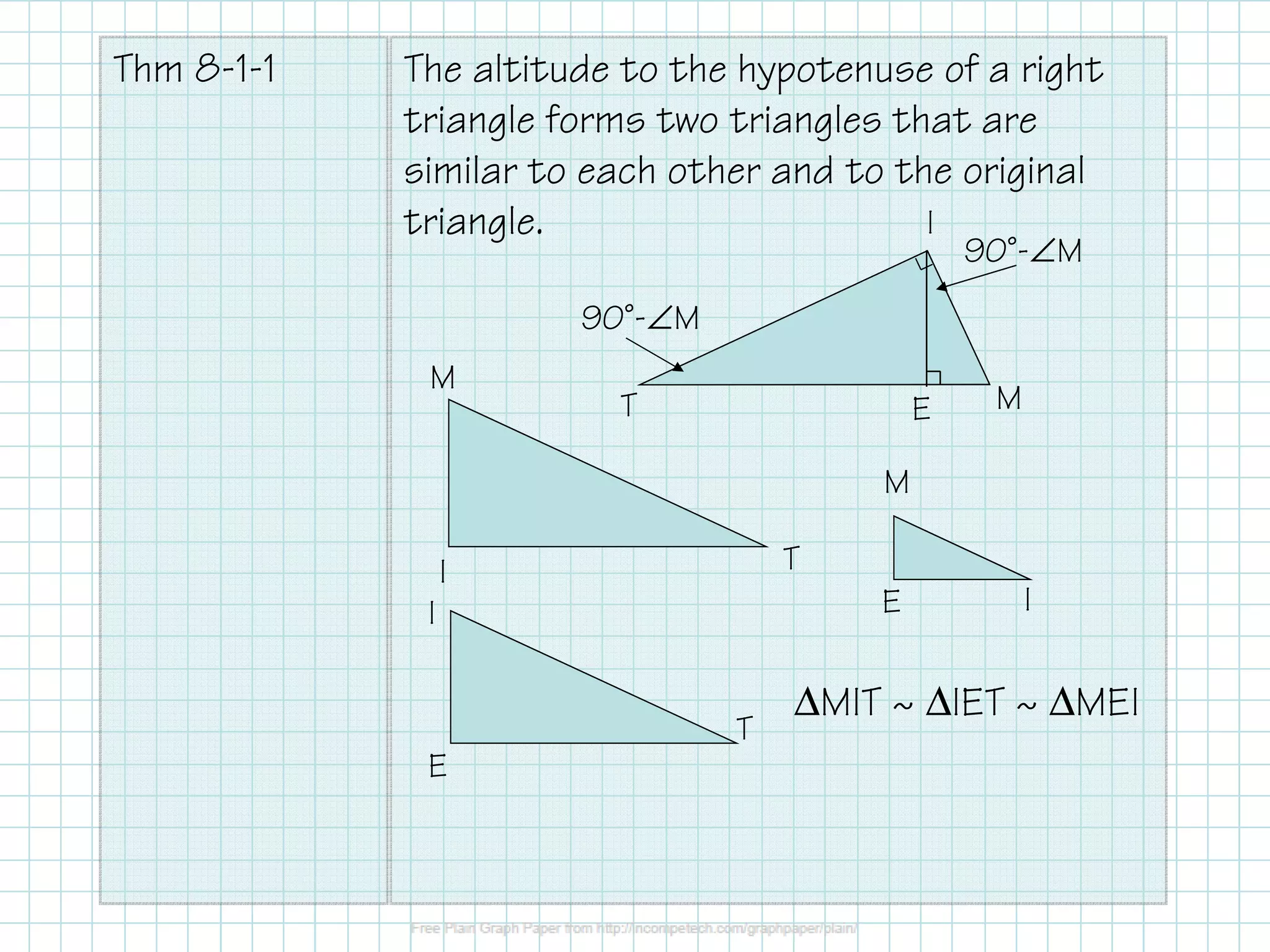
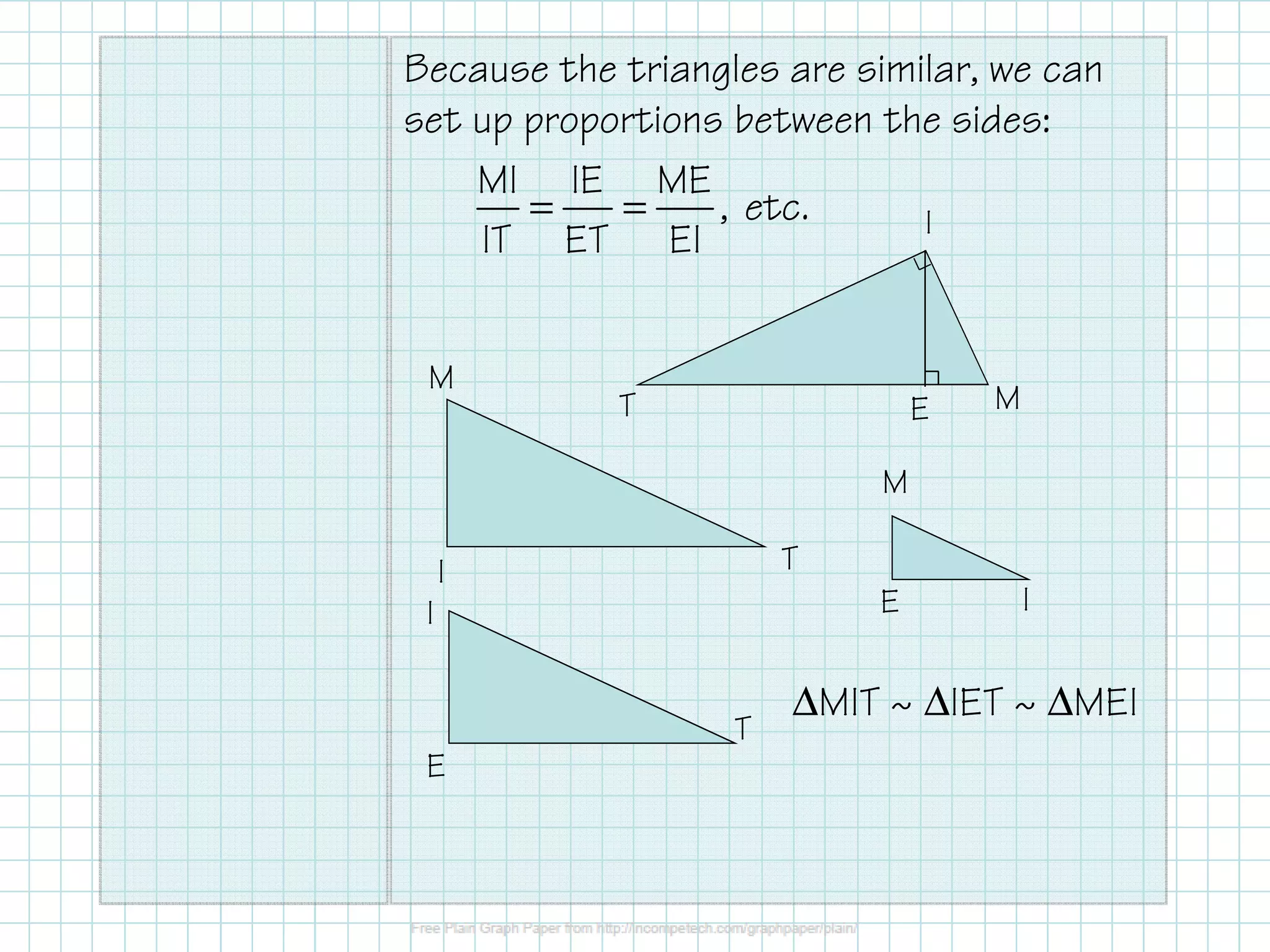
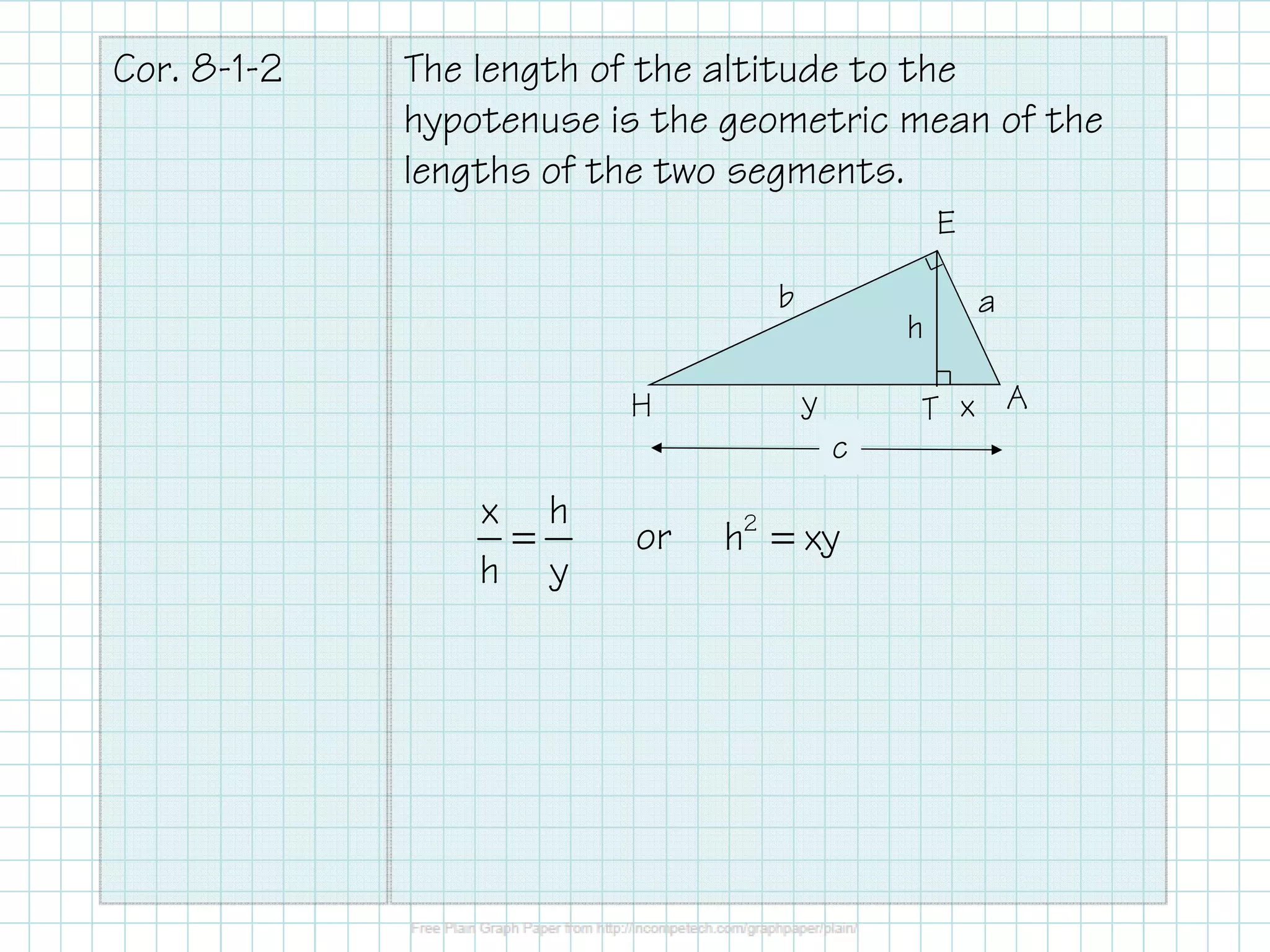
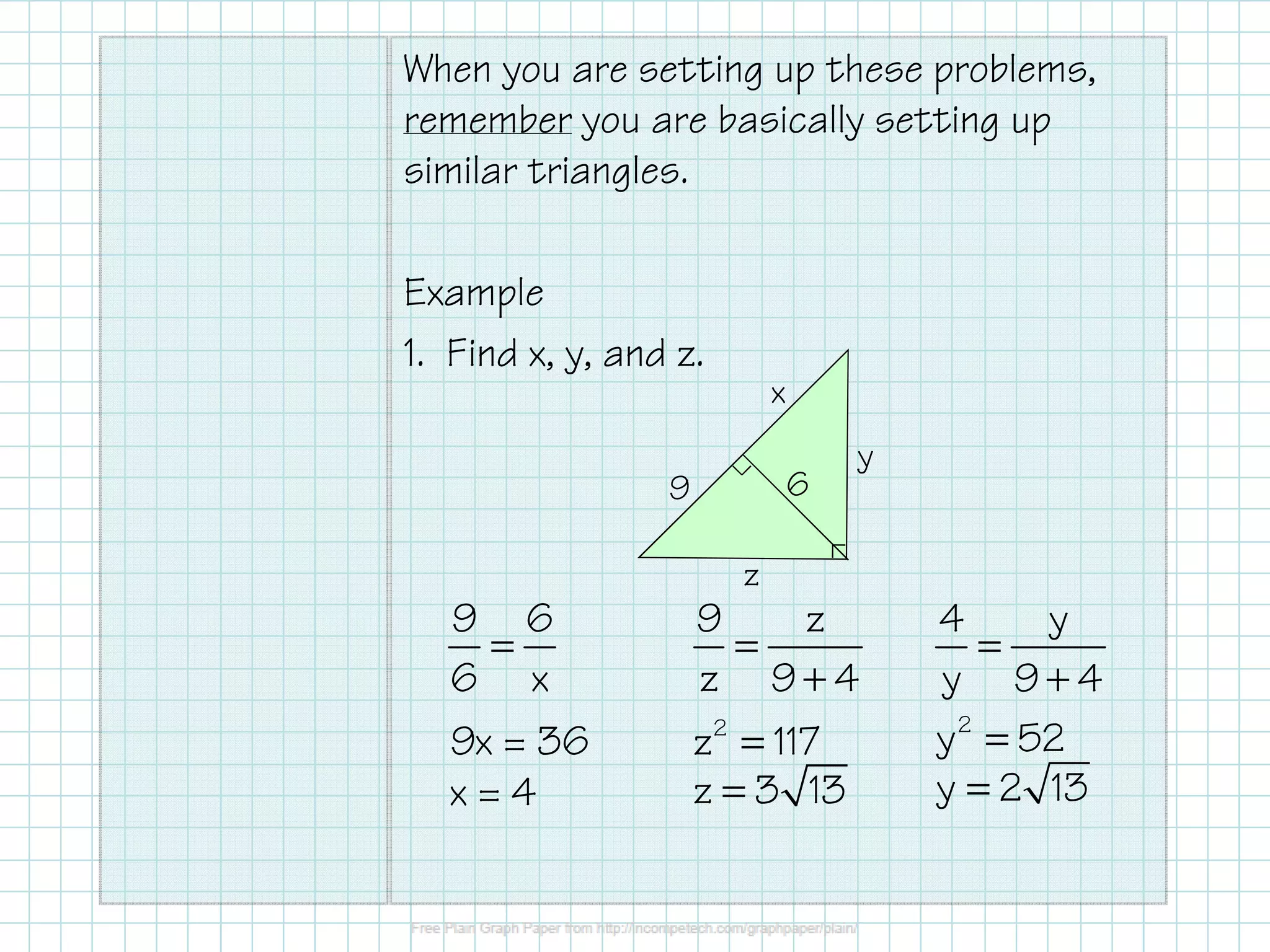
The document discusses the application of geometric means in right triangles, including how to find segment lengths and solve problems using similarity relationships. It explains important theorems related to the altitude to the hypotenuse and the legs of the triangles, highlighting how these are adeptly similar to each other. Examples provided illustrate the calculation of unknown lengths in these triangles.

1. Obj. 39 Similar Right Triangles
The student is able to (I can):
• Use geometric mean to find segment lengths in right
triangles
• Apply similarity relationships in right triangles to solve
problems.

2. geometric
mean
A proportion with the following pattern:
a x
=
x b
or x 2 = ab
or
x = ab
Example: Find the geometric mean of 5 and
20.
5
x
=
x 20
x 2 = 100
x = 10

3. Thm 8-1-1
The altitude to the hypotenuse of a right
triangle forms two triangles that are
similar to each other and to the original
I
triangle.
90˚-∠M
90˚-∠M
M
T
E
M
M
T
I
E
I
T
E
I
∆MIT ~ ∆IET ~ ∆MEI

4. Because the triangles are similar, we can
set up proportions between the sides:
MI IE ME
=
=
, etc.
I
IT ET EI
M
T
E
M
M
T
I
E
I
T
E
I
∆MIT ~ ∆IET ~ ∆MEI

5. Cor. 8-1-2
The length of the altitude to the
hypotenuse is the geometric mean of the
lengths of the two segments.
E
b
H
h
T x A
y
c
x h
=
h y
or
a
h2 = xy

6. Cor. 8-1-3
The length of a leg of a right triangle is the
geometric mean of the lengths of the
hypotenuse and the segment of the
hypotenuse adjacent to that leg.
E
b
H
h
a
T x A
y
c
x a
=
a c
or
a2 = xc
y b
=
b c
or
b 2 = yc

7. When you are setting up these problems,
remember you are basically setting up
similar triangles.
Example
1. Find x, y, and z.
x
6
9
y
z
9 6
=
6 x
9x = 36
x=4
9
z
=
z 9+4
z 2 = 117
z = 3 13
4
y
=
y 9+4
y 2 = 52
y = 2 13