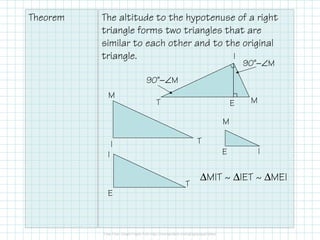
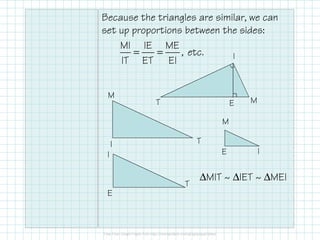
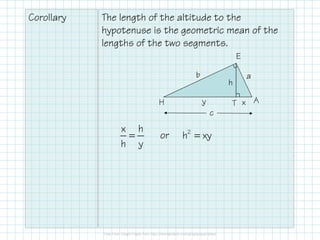
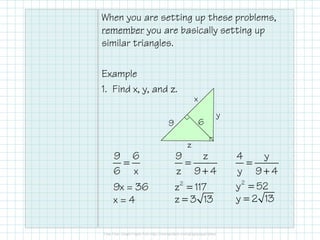
The document explains the concepts of geometric mean and similarity in right triangles, emphasizing how to use these principles to find segment lengths and solve related problems. It specifically discusses the relationship between the altitude to the hypotenuse and the segments it creates, noting that the altitude is the geometric mean of these segments. Furthermore, examples are provided to demonstrate how to apply these relationships to find unknown values in right triangles.

1. Similar Right Triangles
The student is able to (I can):
• Use geometric mean to find segment lengths in right
triangles
• Apply similarity relationships in right triangles to solve
problems.

2. geometric
mean
A proportion with the following pattern:
or or
Example: Find the geometric mean of 5 and
20.
=
a x
x b
=2
x ab =x ab
=
5 x
x 20
=2
x 100
x = 10

3. Theorem The altitude to the hypotenuse of a right
triangle forms two triangles that are
similar to each other and to the original
triangle.
T
I
ME
I T
M
E
I
T
IE
M
90˚−∠M
90˚−∠M
∆MIT ~ ∆IET ~ ∆MEI

4. Because the triangles are similar, we can
set up proportions between the sides:
T
I
ME
I T
M
E
I
T
IE
M
∆MIT ~ ∆IET ~ ∆MEI
= =
MI IE ME
, etc.
IT ET EI

5. Corollary The length of the altitude to the
hypotenuse is the geometric mean of the
lengths of the two segments.
H
E
AT
ab
xy
c
h
=
x h
h y
or =2
h xy

6. The length of a leg of a right triangle is the
geometric mean of the lengths of the
hypotenuse and the segment of the
hypotenuse adjacent to that leg.
H
E
AT
ab
xy
c
h
=
x a
a c
or =2
a xc
=
y b
b c
or =2
b yc

7. When you are setting up these problems,
remember you are basically setting up
similar triangles.
Example
1. Find x, y, and z.
9 6
x
y
z
=
9 6
6 x
9x = 36
x = 4
=
+
9 z
z 9 4
=2
z 117
=z 3 13
=
+
4 y
y 9 4
=2
y 52
=y 2 13