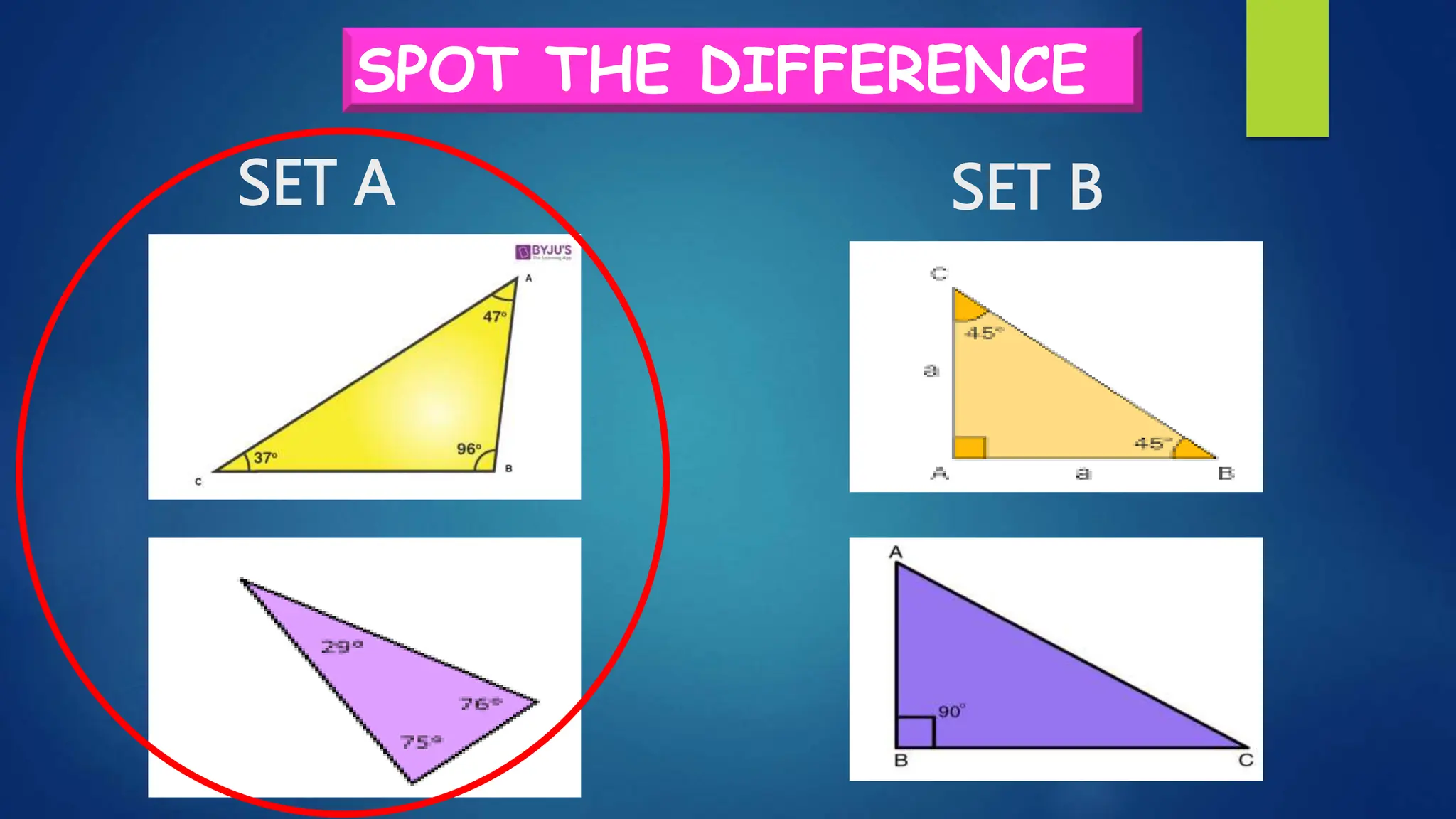
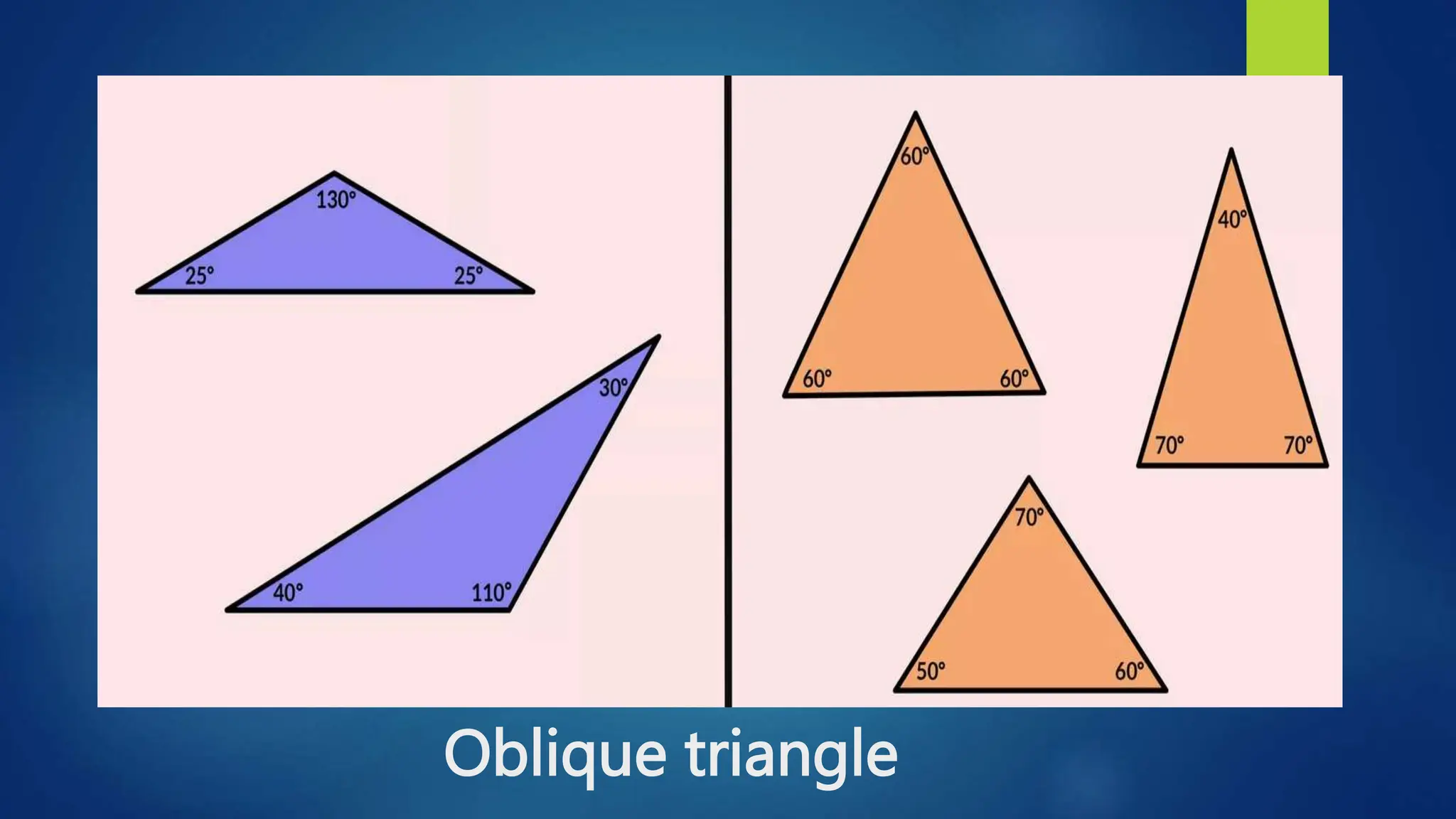
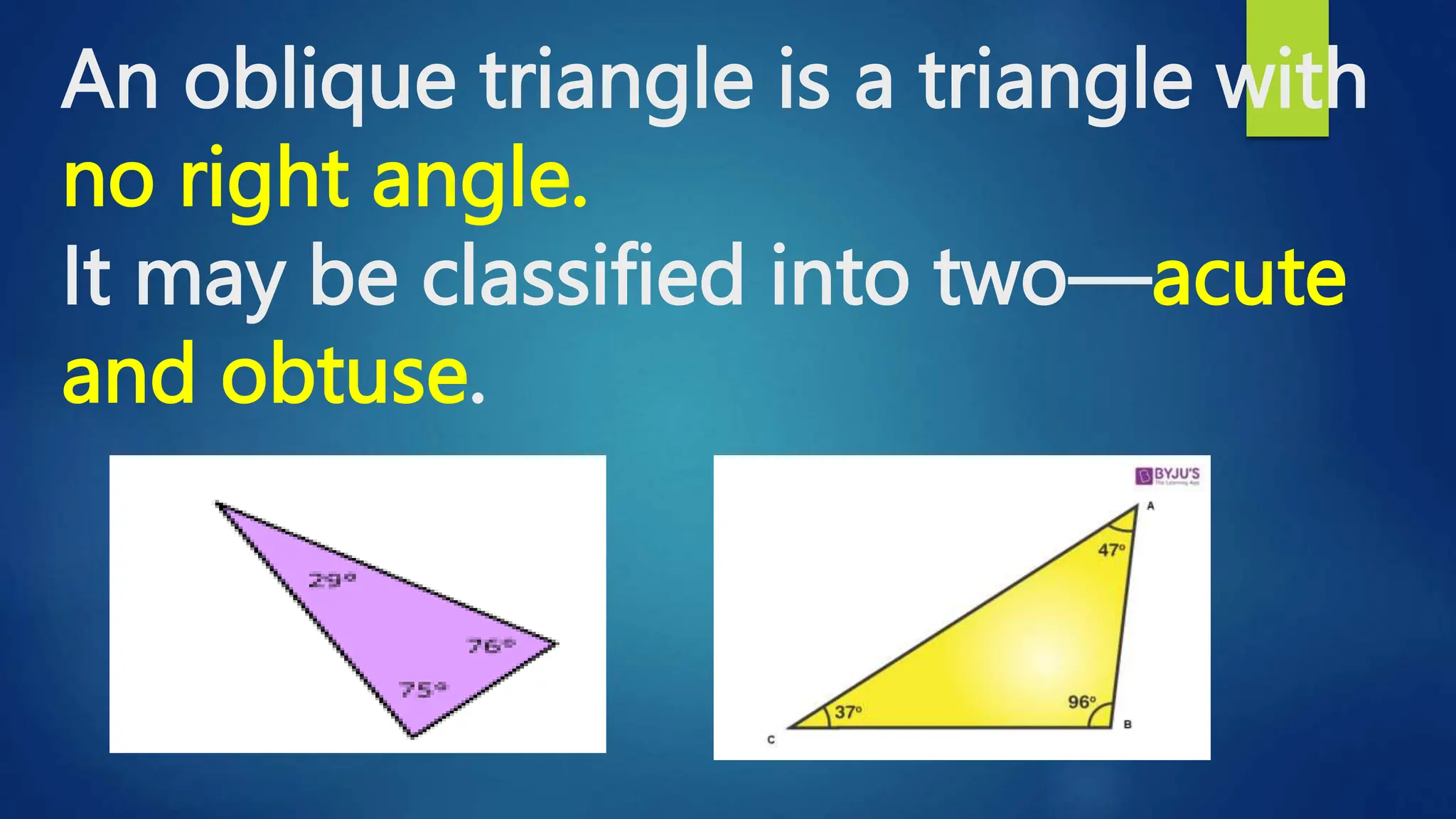
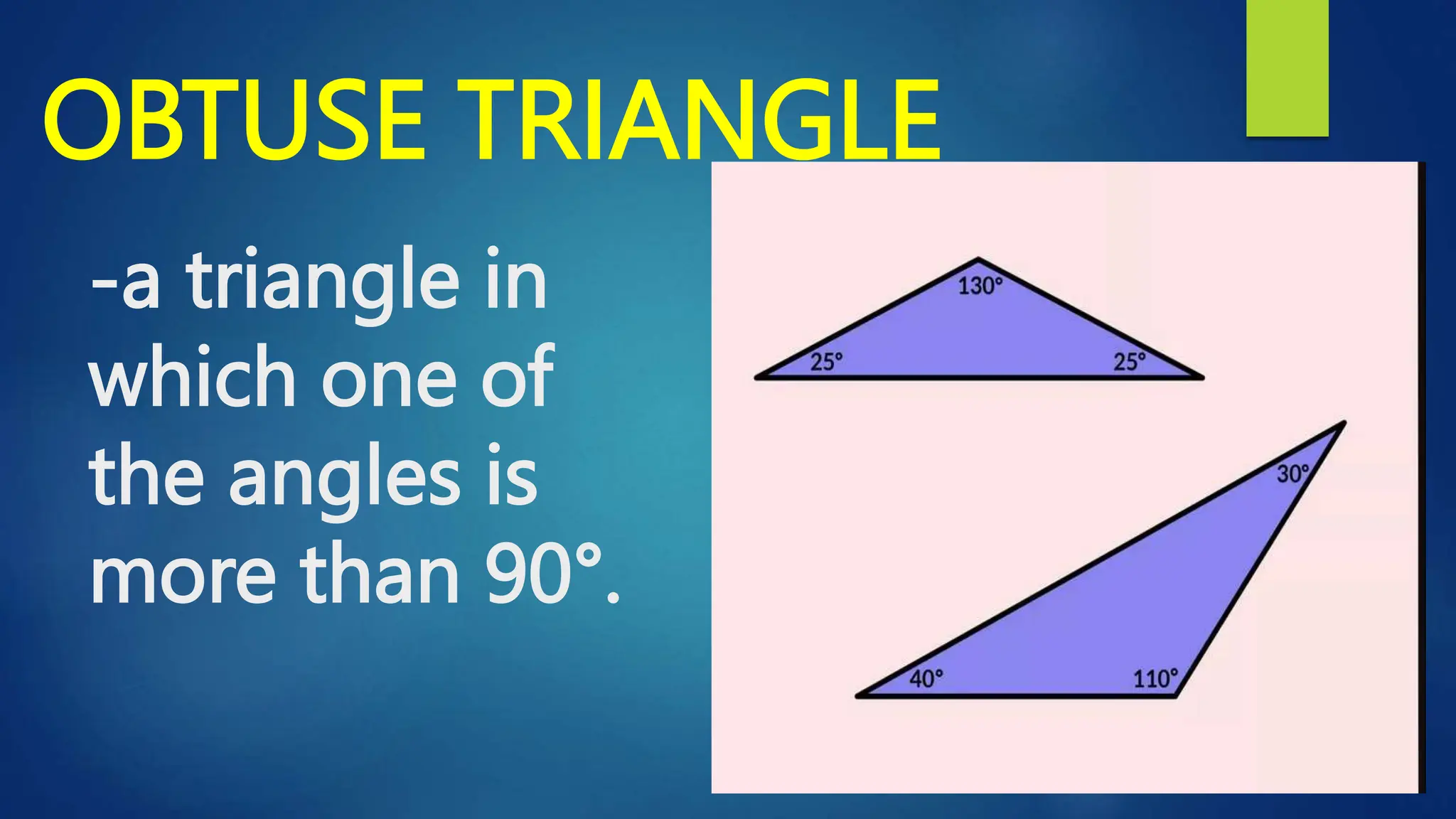
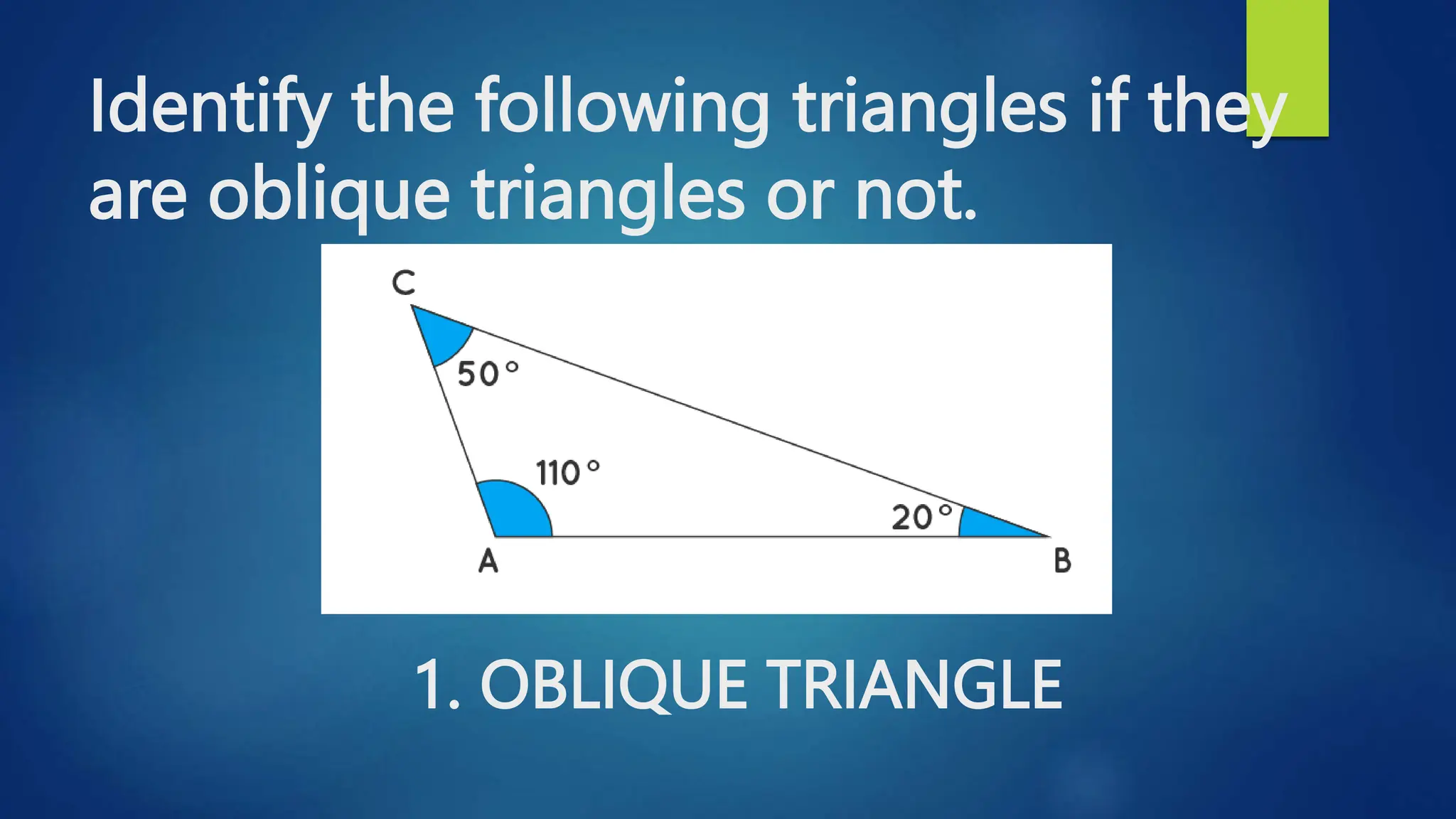
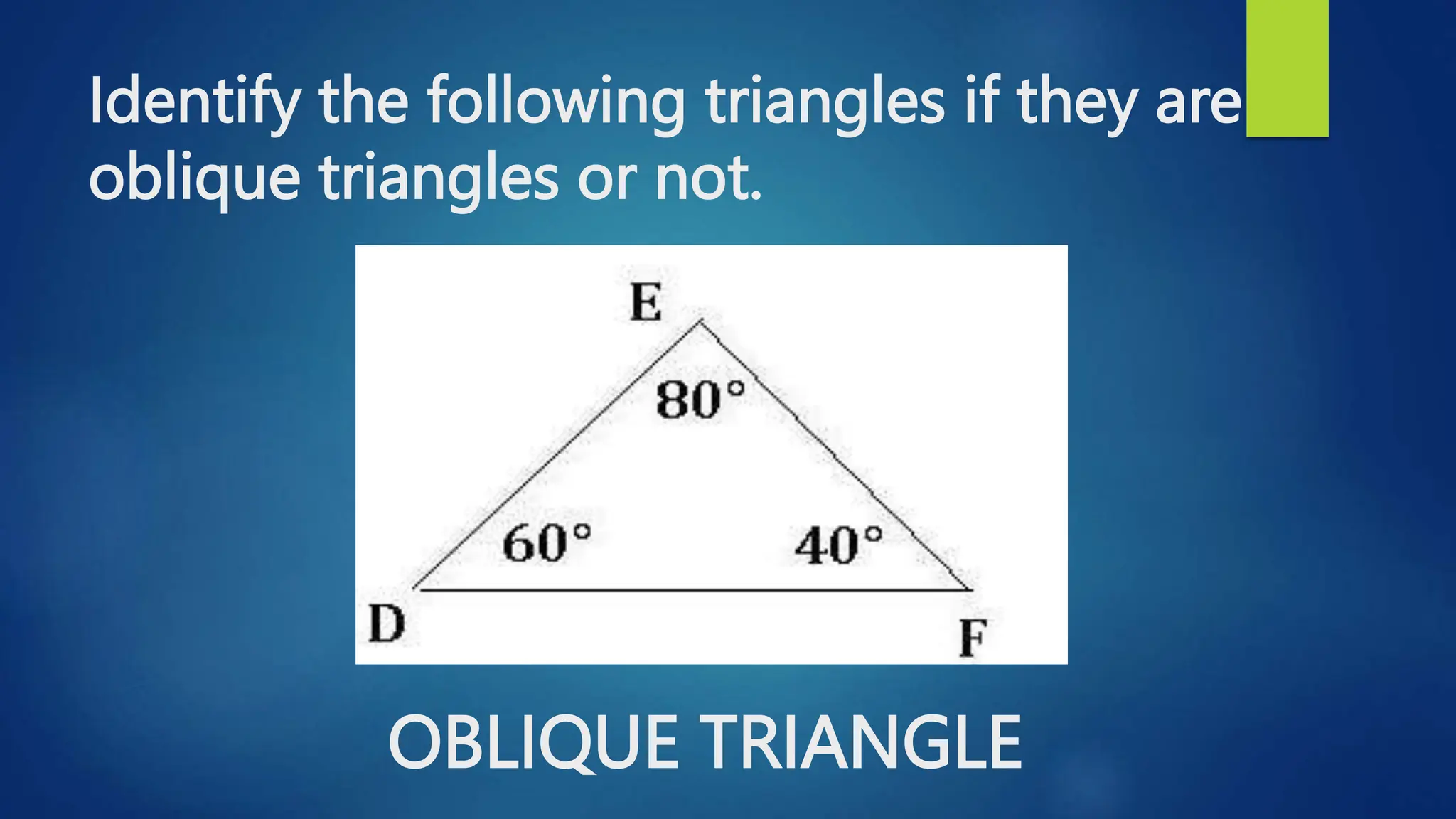
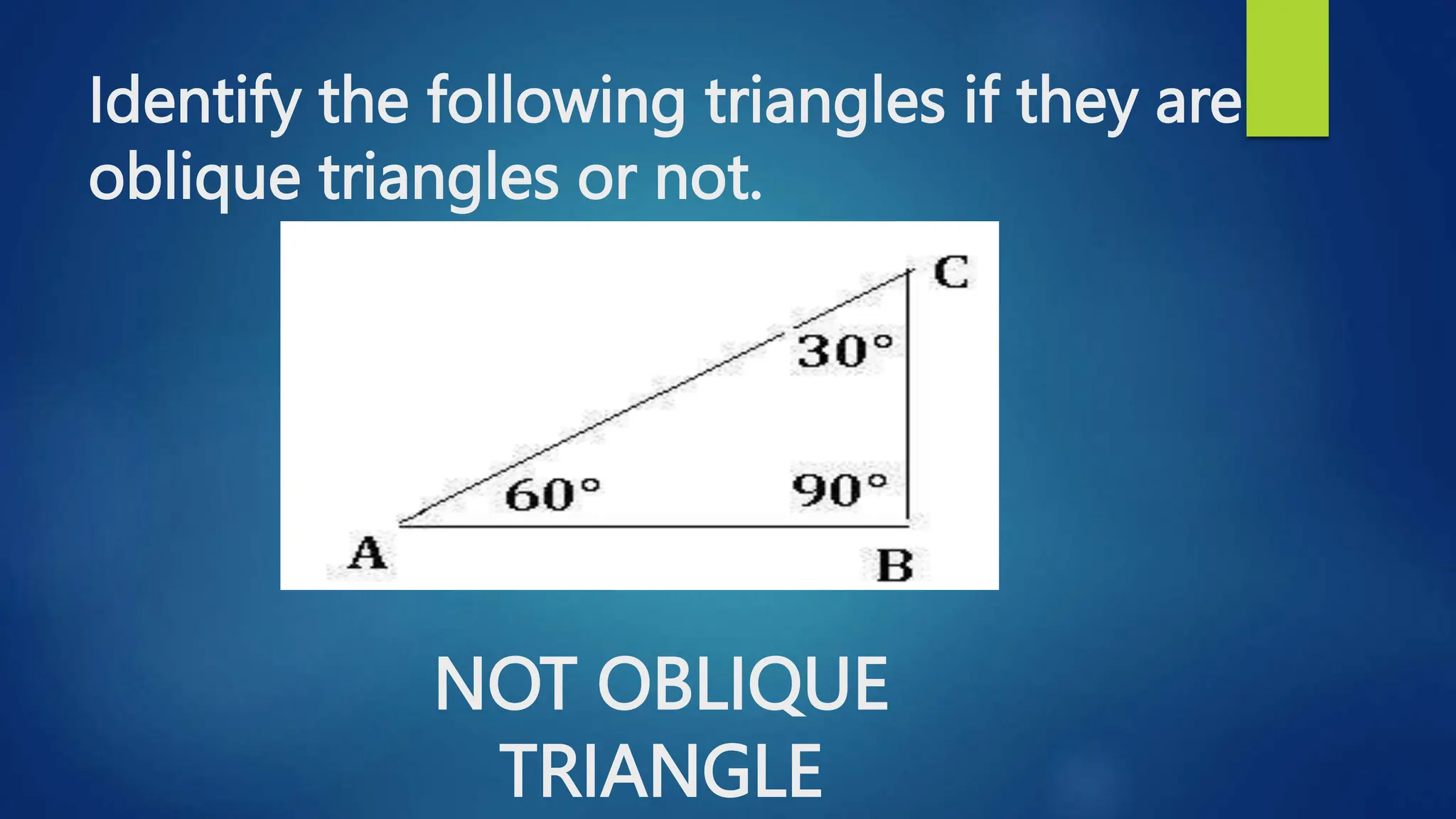
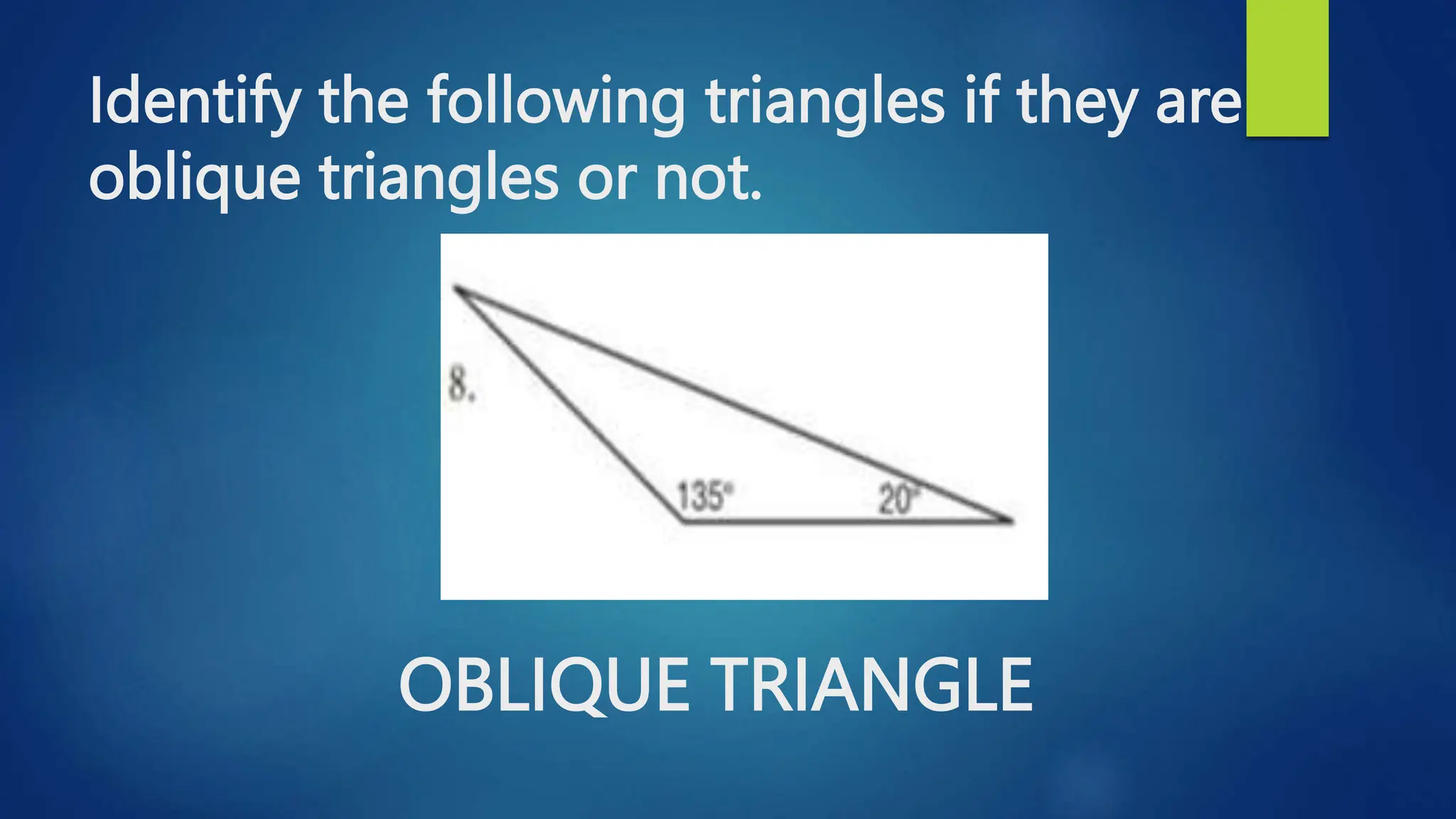
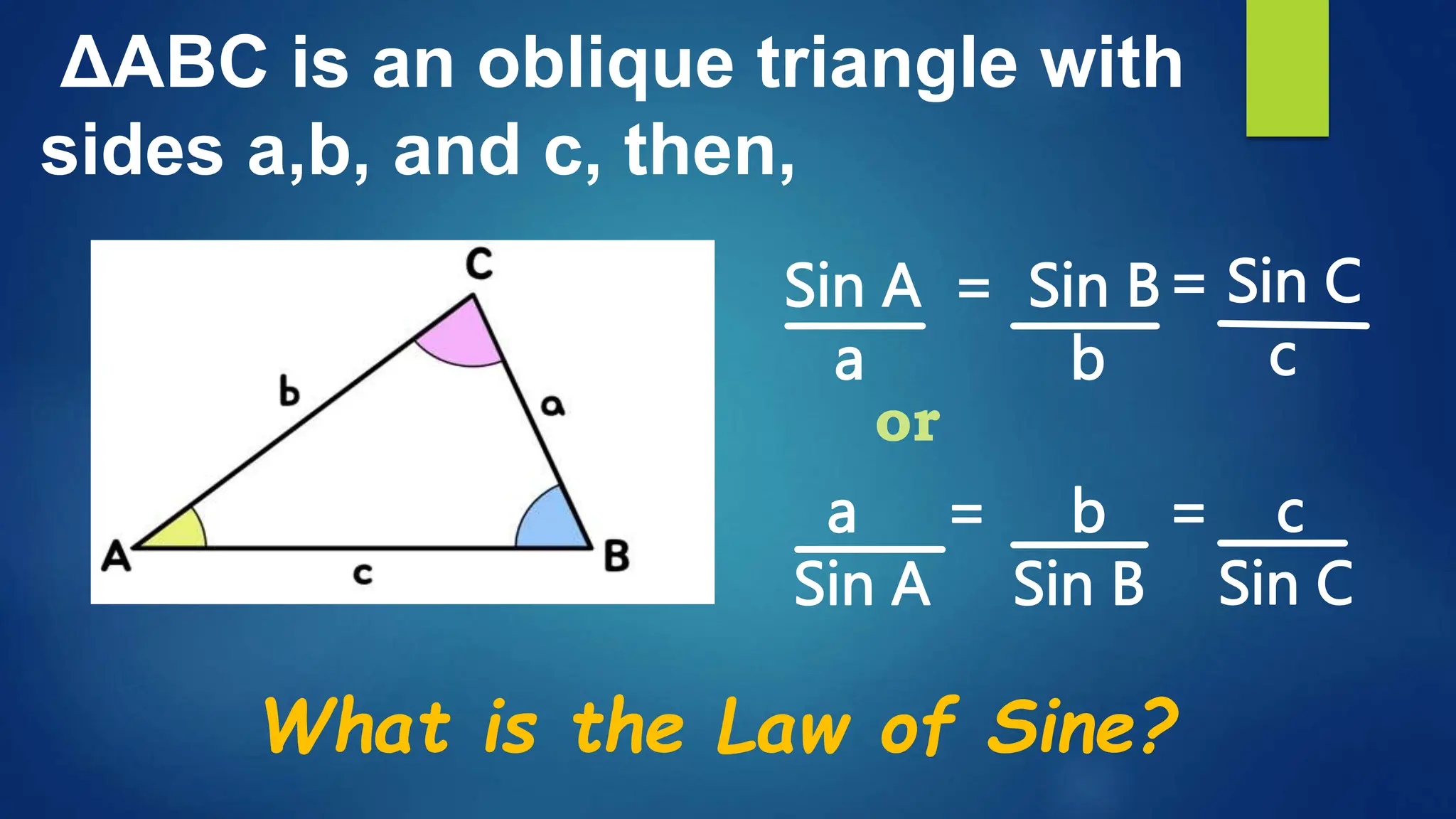
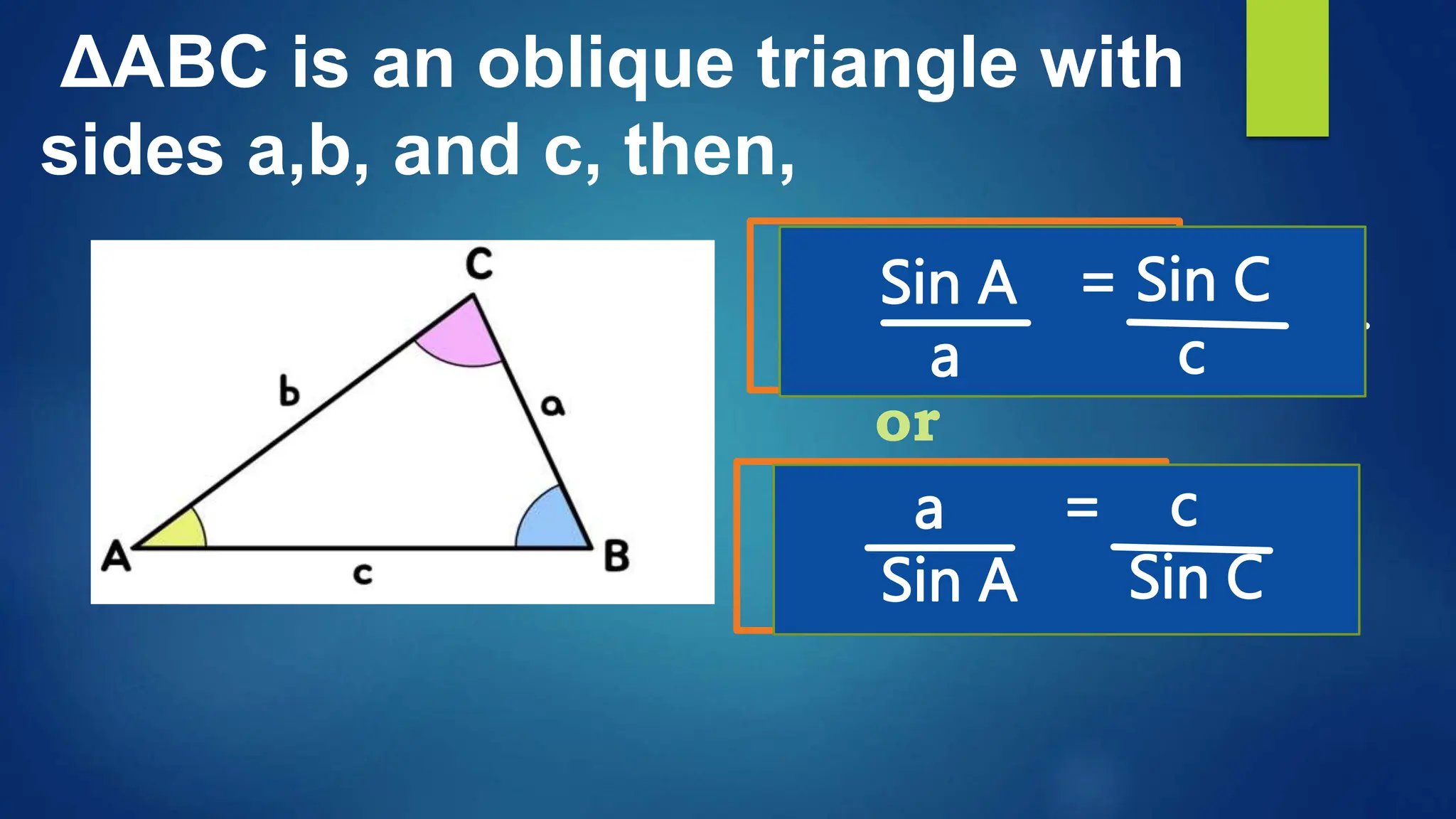
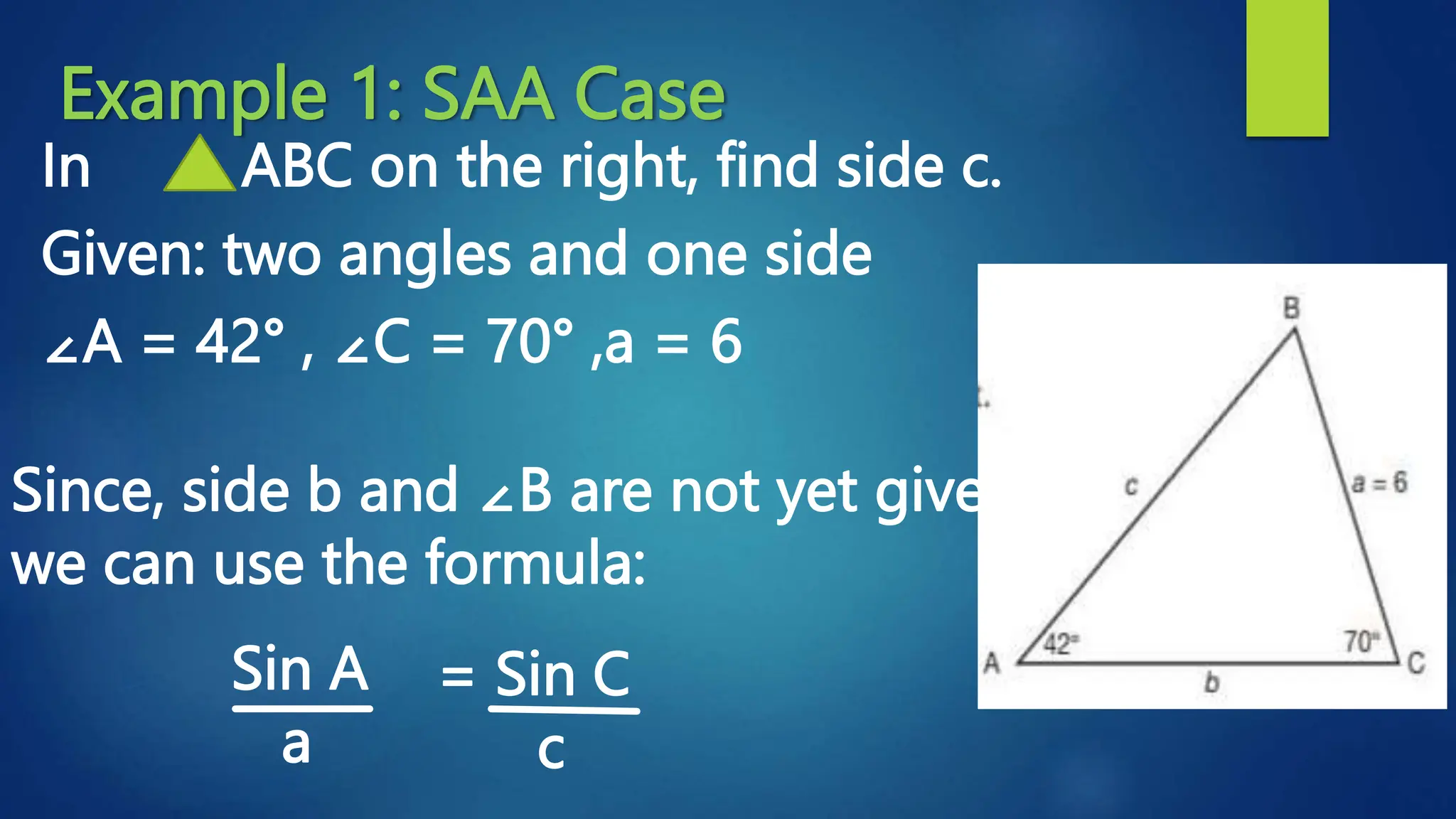
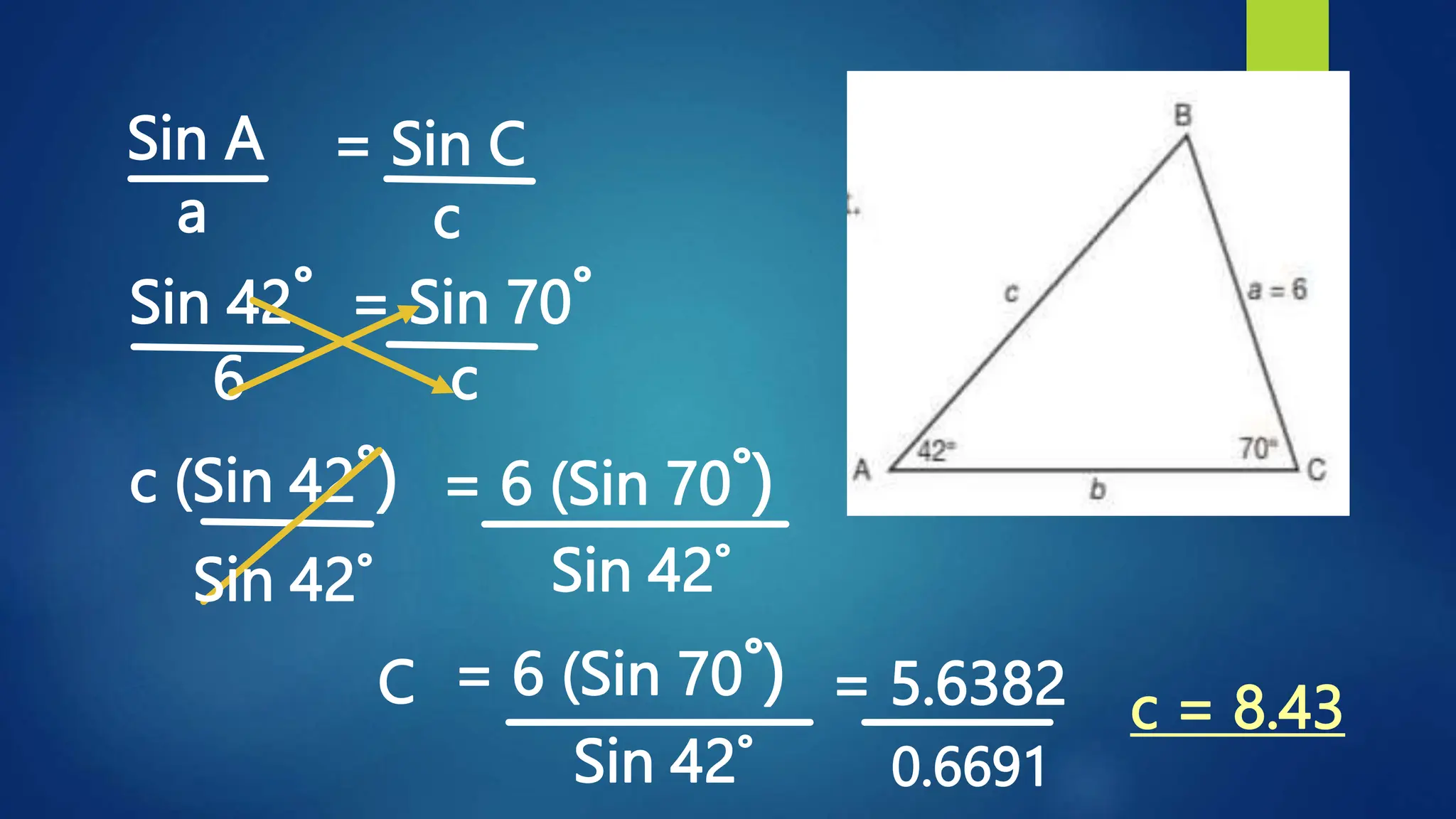
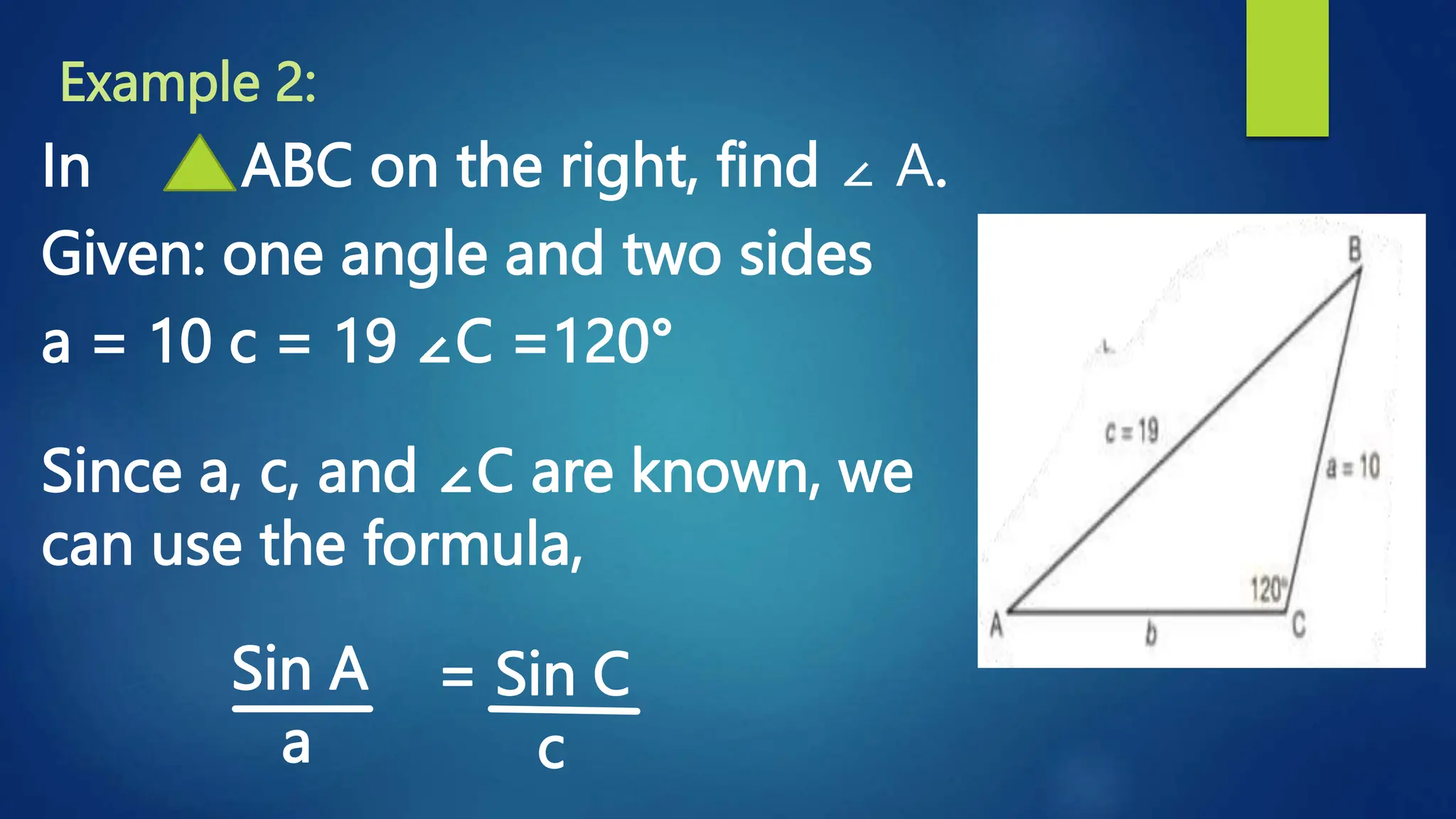
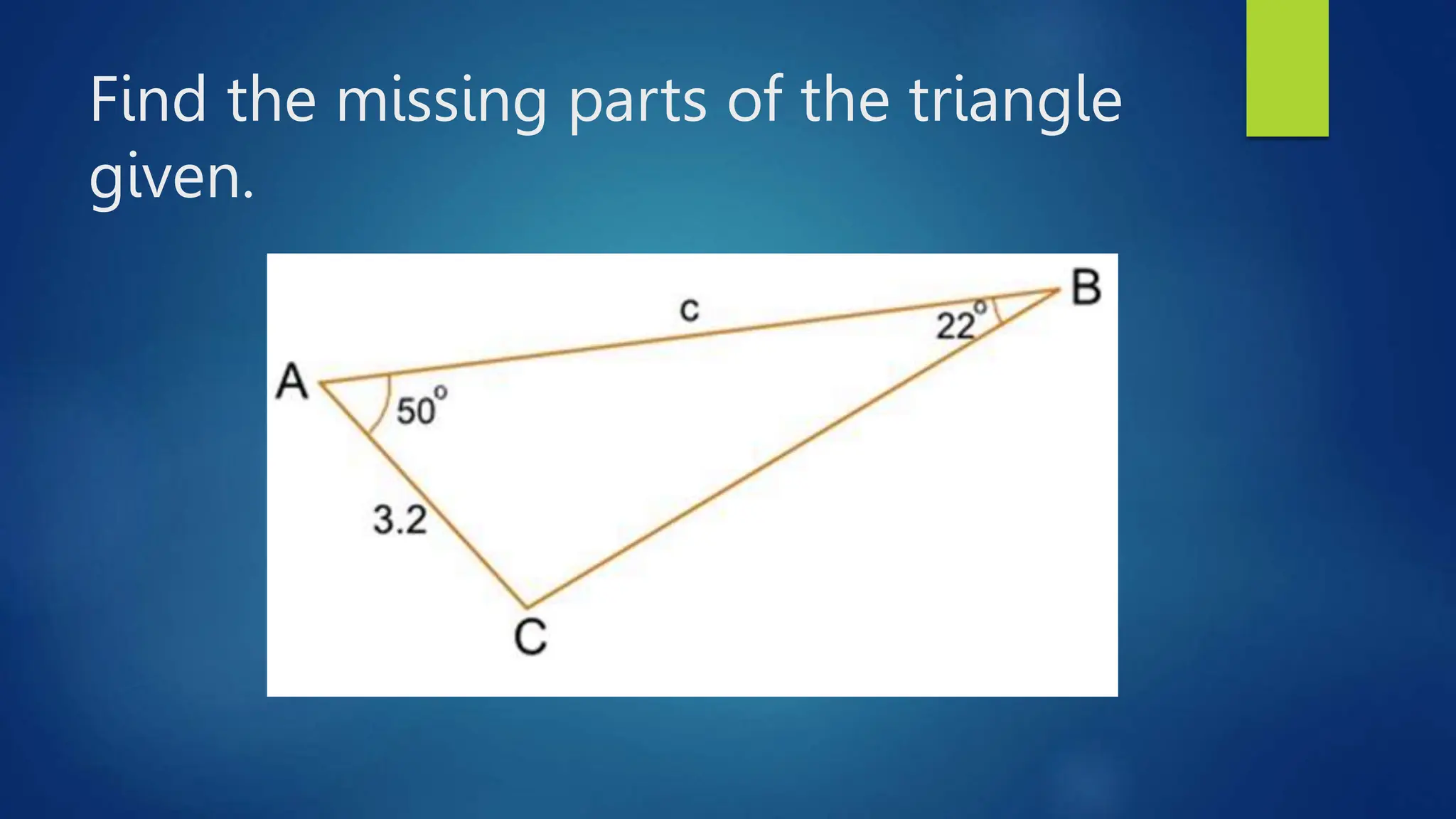
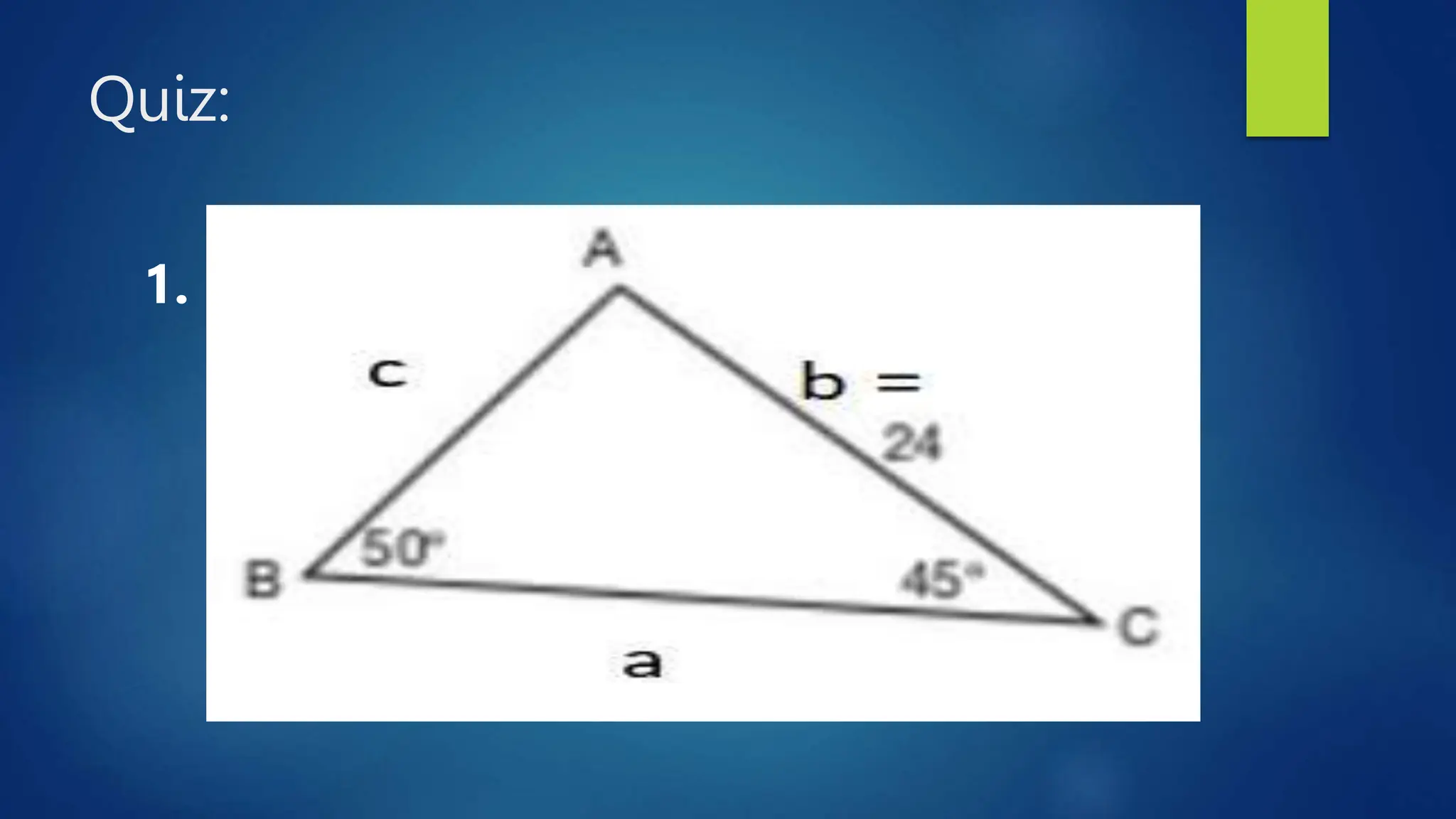
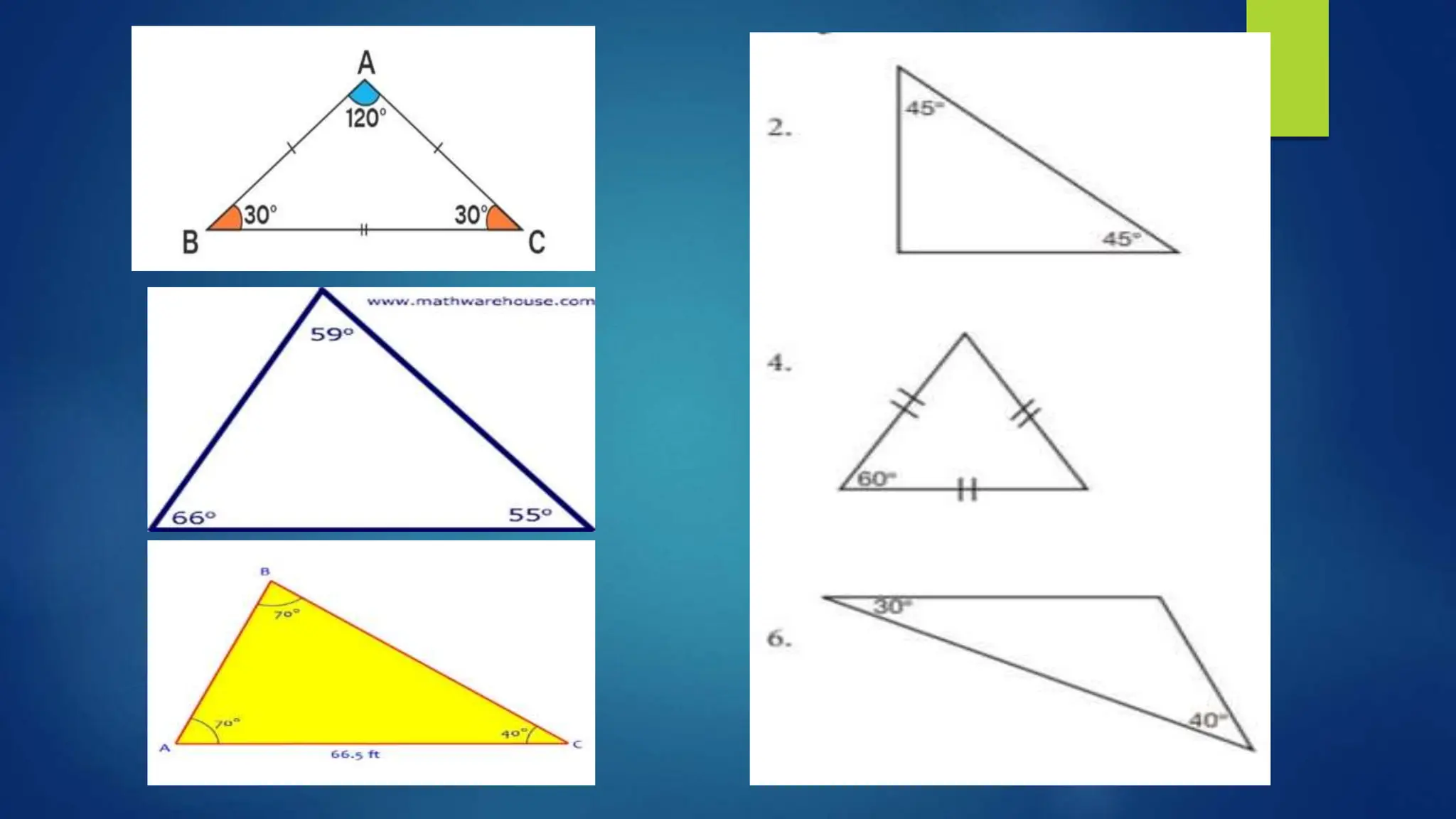
This document discusses oblique triangles and the Law of Sines. It begins by defining oblique triangles as triangles that do not have a right angle. It then introduces the Law of Sines, which states that the ratio of the sine of an angle to its opposite side is equal to the ratio of the sine of any other angle to its opposite side. Examples are given to demonstrate how to use the Law of Sines to solve for missing sides and angles of oblique triangles when given certain information like two angles and a side. Real-world applications of the Law of Sines are also mentioned.

1. PRAYER…

2. REVIEW:
1.What are the 3 classifications of
angles according to degrees?

3. REVIEW:
2.What is an acute angle?

4. REVIEW:
3.What is an obtuse angle?

5. REVIEW:
4.What is a right angle?

6. SPOT THE
DIFFERENCE

7. SET A SET B
SPOT THE DIFFERENCE

8. OBLIQUE TRIANGLES

9. OBJECTIVES:
Identify an oblique triangle,
Illustrate the law of sines, (M9GEIVf-g-1)
Solve the missing sides and angles applying sine
law
Appreciate the importance of the law of sine in
solving problems involving oblique triangles

10. Oblique triangle

11. An oblique triangle is a triangle with
no right angle.
It may be classified into two—acute
and obtuse.

12. Acute Triangle
-a triangle
whose angles
are all less than
90°.

13. OBTUSE TRIANGLE
-a triangle in
which one of
the angles is
more than 90°.

15. Identify the following triangles if they
are oblique triangles or not.
1. OBLIQUE TRIANGLE

16. Identify the following triangles if they are
oblique triangles or not.
OBLIQUE TRIANGLE

17. Identify the following triangles if they are
oblique triangles or not.
NOT OBLIQUE
TRIANGLE

18. Identify the following triangles if they are
oblique triangles or not.
OBLIQUE TRIANGLE

19. Identify the following triangles if they are
oblique triangles or not.
OBLIQUE TRIANGLE

20. Questions:
1. Is it easy to identify the triangles?
Why?
2. How can you identify the oblique
triangles?
3. How about we try to solve the
missing parts of these triangles??

21. Sin A
a
= Sin B
b
= Sin C
c
a
Sin A
= b
Sin B
= c
Sin C
ΔABC is an oblique triangle with
sides a,b, and c, then,
or
What is the Law of Sine?

22. The Law of Sine is the relationship
between the sides and angles of an
oblique triangles .
What is the Law of Sine?

23. Also the Law of Sines states that the
sides of a triangle are proportional to
the sines of their opposite angles.
Law - Rule
SYNONYM

24. a word having the same or
nearly the same meaning as
another word in the same
language.
Example: Law- Rule
SYNONYM

25. GOLDEN RULE:
“Do not do unto others what
you don’t want others do
unto you.”

26. When to use Law of Sine?
It can only be used if the given
triangles are oblique triangles.
It can only be used if the given are :
a. 2 angles and 1 opposite side.
b. 1 angle and opposite side

27. Why is it important to
follow the laws of society?

28. Sin A
a
= Sin B
b
= Sin C
c
= b
Sin B
= c
Sin C
ΔABC is an oblique triangle with
sides a,b, and c, then,
or
a
Sin A
Sin A
a
= Sin C
c
a
Sin A
= c
Sin C

29. EXAMPLES:
1.Given :
Two angles and one opposite
side
(SAA Case) or (ASA Case)

30. In ABC on the right, find side c.
Given: two angles and one side
∠A = 42° , ∠C = 70° ,a = 6
Sin A
a
= Sin C
c
Since, side b and ∠B are not yet given,
we can use the formula:
Example 1: SAA Case

31. Sin A
a
= Sin C
c
Sin 42˚
6
= Sin 70˚
c
c (Sin 42˚) = 6 (Sin 70˚)
C = 6 (Sin 70˚)
Sin 42˚
= 5.6382 c = 8.43
Sin 42˚ Sin 42˚
0.6691

32. In ABC on the right, find ∠ A.
Given: one angle and two sides
a = 10 c = 19 ∠C =120°
Sin A
a
= Sin C
c
Since a, c, and ∠C are known, we
can use the formula,
Example 2:

33. Sin A
a
= Sin C
c
Sin A˚
10
= Sin 120˚
19
19 (Sin A) =10 (Sin 120˚)
Sin A = 10 (Sin 120˚)
19
= 8.66
19
Sin A = 8.66
19
A = Sin -¹ 8.66
19
A = 27.12°
19
= 19

34. What did you learn today?

35. Why is important to study the
Sine Law?
Sine Law is essential in solving oblique
triangles since the trigonometric ratios
involving parts of a right triangle are not
applicable in these types of triangles. It is
very useful in determining the missing
angle or side of an oblique triangle.

36. APPLICATIONS:
One real-life application of the sine
rule is the sine bar, which is used to
measure the angle of tilt in engineering.
In Science, other common examples
include measuring distances in navigation
and the measurement of the distance
between two stars in astronomy.

37. EVALUATION:
https://forms.office.co
m/r/SET9yEWwVk

38. Assignment
Find the missing parts of the triangle.
Find side b, side c and angle A.

39. Find the missing parts of the triangle
given.

40. Quiz:
1.

42. Quiz
 2.