Downloaded 357 times
JP
Uploaded byJuan Miguel Palero
PPTX, PDF9,869 views
Mathematics 9 Lesson 3: Quadratic Functions
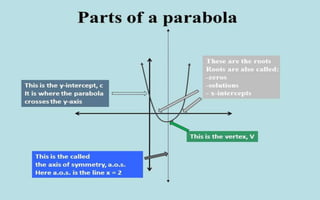
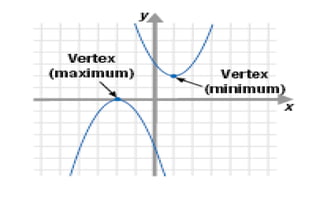
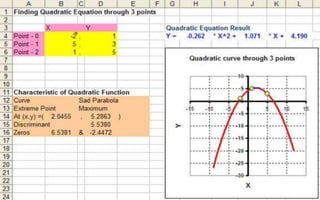
Quadratic functions are polynomial equations of the form f(x) = ax² + bx + c, with specific characteristics based on the value of 'a'. The document explains how to graph a parabola by determining its vertex, axis of symmetry, and intercepts, as well as how to represent the function in vertex form. Essential steps for graphing include finding the vertex, creating a table of values, and plotting points to connect with a smooth curve.
In this document
Powered by AI
Introduces quadratic functions as second-degree polynomials. Their standard and vertex forms are defined, and the parabola representing their graph is explained.
Describes how the orientation of a parabola depends on the coefficient 'a'. Also includes concepts of vertex, axis of symmetry, and its implications in graphing.
Outlines the steps to graph a quadratic function in vertex form, including finding the vertex and intercepts, and plotting them to form a smooth curve.
Continues with methods for graphing quadratic functions, including finding the vertex using the x-coordinate formula, creating a value table, and plotting the graph.
More Related Content
What's hot
Viewers also liked
Similar to Mathematics 9 Lesson 3: Quadratic Functions
More from Juan Miguel Palero
Recently uploaded
Mathematics 9 Lesson 3: Quadratic Functions
- 1.
- 2. QUADRATIC FUNCTION It isa second degree polynomial Equation: f(x) = ax2 + bx + c where a, b, and c are real numbers
- 3. QUADRATIC FUNCTION Vertex FormEquation: f(x) = a(x – h)2 + k where, a ≠ 0
- 4. QUADRATIC FUNCTION Parabola • Itis the graph of the quadratic equation
- 5. QUADRATIC FUNCTION If a> 0, the parabola opens upward If a < 0, the parabola opens downward
- 8. y = a(x-h)2+ k Vertex: (h,k) Axis of Symmetry: x = h
- 9. GRAPHING A PARABOLA WITHEQUATION IN VERTEX FORM To graph f(x) = a(x-h)2 + k 1. Determine whether the parabola opens upward or downward. If a > 0, it opens upward. If a < 0, it opens downward 2. Determine the vertex of the parabola. The vertex is (h, k)
- 10. GRAPHING A PARABOLA WITHEQUATION IN VERTEX FORM 3. Find any x-intercept by replacing f(x) with 0. Solve the resulting quadratic equation for x. 4. Find the y-intercept by replacing x with 0. Solve the resulting equation for y. 5. Plot the intercepts and vertex. Connect these points with a smooth curve
- 11. GRAPHING QUADRATIC FUNCTIONS 1. Determinethe coordinates of the vertex by finding the x-coordinate from the formula x = − b 2a . Substitute the x-coordinate into the original quadratic function, and solve for y to determine the y-coordinate for the vertex
- 12. GRAPHING QUADRATIC FUNCTIONS 2. Determinea table of values by choosing at least two x-values that are greater than the x- coordinate of the vertex and two corresponding x- values that are less than the x-coordinate of the vertex
- 13. GRAPHING QUADRATIC FUNCTIONS 3. Graphthe function by plotting the vertex and the set of ordered pairs from the table of values. Next, connect the points with a smooth curve.