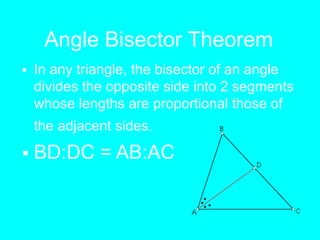
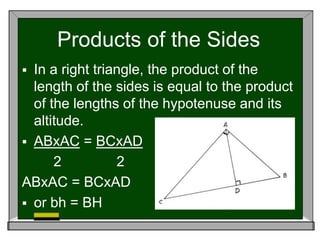
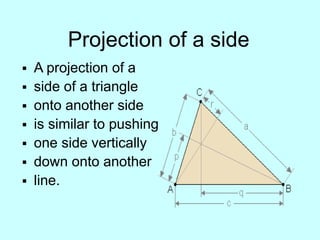
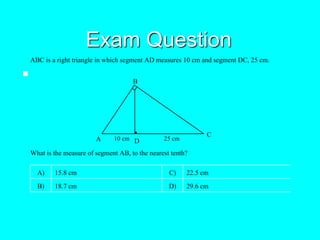
This document covers several metric relationships and theorems related to triangles and right triangles. It discusses concepts like congruency, similarity, angle bisector theorem, Pythagorean theorem, products of sides, geometric mean, altitude to hypotenuse theorem, projections of sides, proportional mean theorem, 30 degree theorem, median theorem, and includes example problems to solve involving right triangles.

1. Metric Relationships
Showings Proofs and
Logical Thinking in Math

2. Proofs
 This topic deals with showing
logical steps as you try to
determine a length or angle in a
triangle or circle.
 You may use the handout.
 Many of the concepts you
already know.

3. Congruency and Similarity
 Only if we can prove that two
triangles are congruent or
similar by (ASA, SAS, etc),
can we then determine the
lengths and angles of the
corresponding sides.

4. Angle Bisector Theorem
 In any triangle, the bisector of an angle
divides the opposite side into 2 segments
whose lengths are proportional those of
the adjacent sides.
 BD:DC = AB:AC

5. Activity
 Page 273, Q. 1, 5a,b, 10

6. Pythagorean Theory
 In a right triangle, the square of the
hypotenuse is equal to the sum of
the squares of the other 2 sides.
 c2 = a2 + b2

7. Corollary to Pythagorean
Theorem
 IF the square of the length of
the longest side of a triangle
IS equal to the sum of the
squares of the lengths of the
other 2 sides, THEN it is a
right triangle.

8. Right Triangle Area
 The area of a triangle is
 A = bh
2
In a right triangle you can
usually find this 2 ways.

9. Products of the Sides
 In a right triangle, the product of the
length of the sides is equal to the product
of the lengths of the hypotenuse and its
altitude.
 ABxAC = BCxAD
2 2
ABxAC = BCxAD
 or bh = BH

10. Geometric Mean
 The geometric mean of 2
numbers is the square root of
their product.
 E.g. 4, 9….4x9 = 36
 So the geometric mean is √36
 Which is 6.

11. Altitude to the Hypotenuse
Theorem
 The length of the altitude to
 the hypotenuse of a right
 triangle is the geometric
 mean between the lengths
 of the segments into which
 the altitude divides the
 hypotenuse.
 m2 = 3x7

12. Projection of a side
 A projection of a
 side of a triangle
 onto another side
 is similar to pushing
 one side vertically
 down onto another
 line.

13. Proportional Mean Theorem
 In a right triangle, each side is
the geometric mean between
the hypotenuse and that
side’s projection on the
hypotenuse.

14. 30˚ Theorem
 If a right triangle contains a 30˚ angle, the
side opposite the 30˚ angle is ½ the
length of the hypotenuse.

15. Median Theorem
 In a right triangle, the length of the
median to the hypotenuse is equal to ½
the length of the hypotenuse.

16. Exam Question

ABC is a right triangle in which segment AD measures 10 cm and segment DC, 25 cm.
A
B
C
D10 cm 25 cm
What is the measure of segment AB, to the nearest tenth?
A) 15.8 cm C) 22.5 cm
B) 18.7 cm D) 29.6 cm

17. Exam Question
Given the right triangle to the right.
AB
C
a
b
h
nm
c
Which of the following relations is true?
A) a  b = m  n C) h = m  n
B) a + b = c D) a2
= m  c

18. Exam Question
ABC is a right triangle in which segment AD measures 5 cm and segment DC, 10 cm.
A
B
C
D5 cm 10 cm
What is the measure of segment BD, to the nearest tenth?
A) 7.1 cm C) 8.1 cm
B) 7.6 cm D) 8.6 cm

19. Activity
 Page 282, Q. 7, 8 a-f, 16, 18