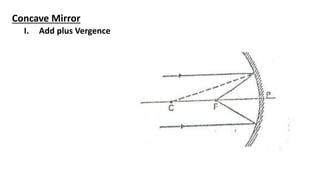
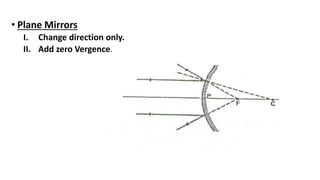
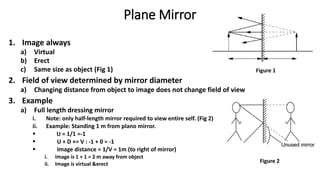
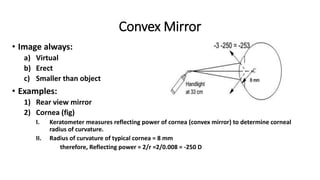
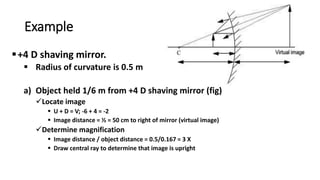
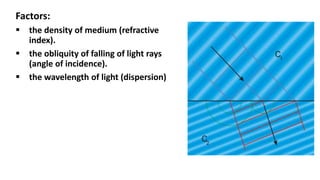
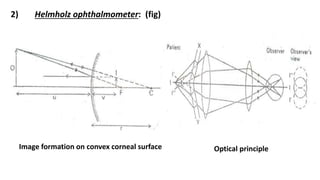
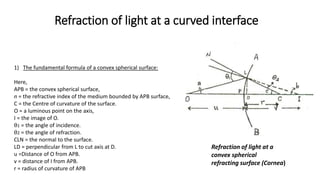
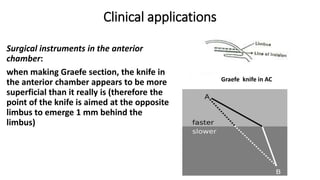
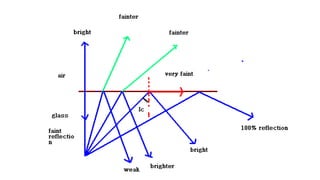
This document discusses reflection and refraction at surfaces and curved surfaces. It begins by explaining the fundamentals of reflection, refraction, and total internal reflection. It then discusses the laws of reflection and refraction. Specific examples of reflection and refraction are provided for plane mirrors, convex mirrors, concave mirrors, and refraction through lenses and the cornea. Clinical applications of reflection and refraction in the eye and optical instruments are described.

1. Reflection and refraction at
home surfaces & curved surfaces
Mohammad Arman Bin Aziz
Instructor (Optometry)
Institute of Community Ophthalmology

2. Reflection
Narcissus, by Michelangelo Caravaggio, ca. 1598.

3. Fundamentals
• When light an interface between two media, its behavior depends on the
nature of the two media involved and so one of the following events may
happen:
1. Absorption: of light by the new medium which is called opaque
medium.
2. Reflection: of light back into the first medium.
3. Transmission: of light onward through the new medium.
4. Some combination of the above: occurs to some degree at all interfaces.

4. Reflection
• It is the sent back of light at an interface between two media into
the first medium.
• E.g. light reflection by mirrors

5. Laws of Reflection
• Two laws which govern reflection of light
1. The incident ray, the reflected ray and the normal to the reflecting
surface all lie in the same plane.
2. The angle of incidence i equals the angle of reflection r.

6. Reflection by the Reflecting surface (Mirror)
A mirror is a part of a hollow sphere whose one side is polished.
1. ‘Lens’ that flips over image space by reversing the direction of light
2. Some mirror also change vergences of light.
Convex Mirror
I. Add minus Vergence.
Concave Mirror

7. Concave Mirror
I. Add plus Vergence

8. • Plane Mirrors
I. Change direction only.
II. Add zero Vergence.

9. How to calculate Vergence added my Mirror???
• Formula:
U + D = V
a) Power (D) is Determined by curvature of surface
b) D (reflecting) = 2/r (Fig)
I. f = focal length of mirror
II. r = radius of curvature of mirror
III. Since light bounces off of mirror, no refractive index to worry
about
Compare with formula for refracting power, D (refracting) = (n’-
n)/r
IV. Example: concave mirror with 50 cm radius of curvature
D = 2/0.5 =4D
 +4 D since it is a concave mirror
• A convex mirror with same radius of curvature is -4 D

10. Plane Mirror
1. Image always
a) Virtual
b) Erect
c) Same size as object (Fig 1)
2. Field of view determined by mirror diameter
a) Changing distance from object to image does not change field of view
3. Example
a) Full length dressing mirror
i. Note: only half-length mirror required to view entire self. (Fig 2)
ii. Example: Standing 1 m from plano mirror.
 U = 1/1 =-1
 U + D += V : -1 + 0 = -1
 Image distance = 1/V = 1m (to right of mirror)
i. Image is 1 + 1 = 2 m away from object
ii. Image is virtual &erect
Figure 1
Figure 2

11. Convex Mirror
• Image always:
a) Virtual
b) Erect
c) Smaller than object
• Examples:
1) Rear view mirror
2) Cornea (fig)
I. Keratometer measures reflecting power of cornea (convex mirror) to determine corneal
radius of curvature.
II. Radius of curvature of typical cornea = 8 mm
therefore, Reflecting power = 2/r =2/0.008 = -250 D

12. Example:
10 cm illuminated target held 1/3 m from cornea.
a) Locate image:
• U =1/0.1 = -3
• U + D = V; -3 + (-250) = -253
• 1/253 = 0.004 = 4 mm (behind cornea)
a) Determine magnification:
• Magnification = image distance / object distance = 4/333 = 0.012 X
• Image size =10 cm × 0.012 = 0.12 cm = 1.2 mm
Summary: if cornea with 8 mm radius of curvature is illuminated with 10 cm
object at distance of 1/3 m, the reflection will be 1.2 mm high and 4 mm
behind the surface of the cornea.
• Image is virtual & erect.

13. Concave Mirror
• Image can be
a) Virtual or real
b) Erect or inverted
c) Smaller or larger
d) Depends on where object and image are with respect to center of
curvature of mirror
• Experiment with ordinary shaving mirror to see how image changes from
upright to inverted depending on object distance.

14. Example
+4 D shaving mirror.
 Radius of curvature is 0.5 m
a) Object held 1/6 m from +4 D shaving mirror (fig)
Locate image
 U + D = V; -6 + 4 = -2
 Image distance = ½ = 50 cm to right of mirror (virtual image)
Determine magnification
 Image distance / object distance = 0.5/0.167 = 3 X
 Draw central ray to determine that image is upright

15. c) Object held 1/3 m from +4 D shaving mirror (Fig)
1) Locate Image
 U + D = V; -3 + 4 = +1
 Image distance = 1/1 =1m to left of mirror (real Image)
2) Determine magnification
 Image distance/ object distance =1/0.33 = 3 X
 Draw central ray to determine that image is inverted

16. d) object held 1 m from +4 D shaving mirror
1) Locate Image
 -1 + 4 = +3
 Image distance = 1/3 =33cm to left of mirror (real image)
2) Determine magnification
 Image distance / object distance = 0.33/1 = 0.33 X
 Draw central ray: image is inverted

17. Clinical Applications of Reflecting Surface
 Reflecting Surfaces of eye:
 Keratometer: using the principle that the anterior surface of the cornea acts as
convex mirror to measure the radius of curvature of the cornea.
 Catoptric images (Purkinje’s image): are the images formed by the reflecting
surfaces of the eye.
 Reflecting mirror:
 Concave mirror:
 Distant direct method at 22 cm.
 Direct ophthalmoscopy
 Indirect ophthalmoscopy
 Plane mirror:
 Retinoscopy.
 Stereoscopes .
 Synoptophores.

18. Refraction
Two images of a rose created by the same lens and recorded with the same camera

19. Basics of Refraction
 Bending of light rays
 Is the change in the direction of light when it
passes from one transparent medium into
another of different optical density (the
incident ray, the refracted ray and the
normal all lie in the same plane).

20. Factors:
 the density of medium (refractive
index).
 the obliquity of falling of light rays
(angle of incidence).
 the wavelength of light (dispersion)

21. Law’s of Refraction
1. The incident ray, refracted ray and the normal all lie in the same plane.
2. The angles of incidence i and refraction r are related to the refractive
index n of media concerned by the equation:
i. n = sin i / sin r ; where n is the refractive index of the second medium and when
first medium is air.
ii. n2 / n1 = sin i / sin r ; where n2 is the refractive index of the second medium and n1
is the refractive index of the first medium.
3. The incident and refracted rays are on opposite sides of the normal.

22. Refraction of light through parallel-sided plate
of glass
• Principle: (Fig)
1. Light passing obliquely through plate of
glass is deviated laterally and the emerging
ray is parallel to the incident ray (i.e. the
angle of incidence equals angle of
emergence) and so the direction of light is
unchanged but is laterally displaced.
2. Deviation of light is more with greater
thickness of the glass plate (block) but its
intensity is less. Refraction of light
through a parallel sided
plate of glass

23. Clinical Applications
1. A sheet of glass can be used as an image splitter: as in the
teaching mirror of the indirect ophthalmoscope in which:
a) Most of light is refracted across the glass sheet to the examiner’s eye.
b) A small portion of light is reflected at the anterior surface of the glass
sheet and enables an observer to see the same view as the examiner (fig)
Parallel sided glass

24. 2) Helmholz ophthalmometer: (fig)
Image formation on convex corneal surface Optical principle

25. Refraction of light at a curved interface
1) The fundamental formula of a convex spherical surface:
Here,
APB = the convex spherical surface,
n = the refractive index of the medium bounded by APB surface,
C = the Centre of curvature of the surface.
O = a luminous point on the axis,
I = the image of O.
θ1 = the angle of incidence.
θ2 = the angle of refraction.
CLN = the normal to the surface.
LD = perpendicular from L to cut axis at D.
u =Distance of O from APB.
v = distance of I from APB.
r = radius of curvature of APB
Refraction of light at a
convex spherical
refracting surface (Cornea)

26. Calculation
1. n = sin i / sin r so, sin i = n sin r
2. The sines of the angle of incidence and of refraction equal to their numerical values
as both are small angles (when PD is considered as a small region).
3. θ1 = a + c and θ2 = c – b and a + c = n (c-b).
4. As the angles a, b and c are small and can be replaced by their tangents (remembering
that v and r are negative). So, a = LD/PO = LD/u, b = LD/PI = LD/(-v) and c = LD/PC =
LD/(-v) .
5. Substituting in the above a + c = n (c-b):
LD/u + LD/(-r) = n (LD/ -r) – (LD/ -v)
6. Dividing by LD to get the fundamental formula of a convex spherical surface.
1/u + 1/ -r = n i.e. 1/ u – 1/r = n (-1/r + 1/v) i.e. 1/u – 1/r = -n/r + n/v i.e. n/v – 1/u = n/r – 1/r
so, n/v – 1/u = n-1/r
7. If u is at ∞, v will be at principle focus F (i.e. at focal distance f) so, f = n r/n-r
8. When light is refracted from a medium of n1 to another n2, n becomes n1/n2 and
n2/n1 so, f1 = n1 r/ n2-n1 and f2 = n2 r/n2-n1 where, f1 and f2 are the
anterior and posterior focal distance.

27. 2) The surface refracting power of a convex surface:
1. It is given by the formula, Surface refracting power = n2-n1/r,
where r = the radius of curvature of the surface in meters, n2 =
refractive index of the 2nd medium & refractive index of the 1st
medium.
2. The surface refracting power is measured in diopters which is
positive for converging surfaces and negative for diverging
surfaces.
3. The anterior surface of the cornea is an example of such a
refracting surface and its power accounts for most of refracting
power the eye.

28. Real and apparent depth
• Principle:
1. Objects situated in an optically dense medium
appear displaced when viewed from a less
dense medium (fig) due to the refraction of the
emerging rays which now appear to come from
a point I, the virtual image of object O.
2. Ref index of water = velocity of light in air/water
= 4/3.
3. Practically it is not necessary to find the 2
velocities directly as both can be replaced by
the real and apparent depth which are easily
found and so,
4. Objects in water seem less deep than are e.g.
one’s toes in the bath.

29. Clinical applications
Surgical instruments in the anterior
chamber:
when making Graefe section, the knife in
the anterior chamber appears to be more
superficial than it really is (therefore the
point of the knife is aimed at the opposite
limbus to emerge 1 mm behind the
limbus)
Graefe knife in AC

30. Total Internal Reflection
• Rays emerging from a denser medium to a less dense medium (as
from glass to air) suffer a variety of facts depending on the angle of
incidence.
• The angle of incidence must be greater than critical angle, when
refracted angle marked 90 degree.

32. Clinical application
1.The total internal reflection occurs at surfaces
within the eye (notably the cornea-air interface) and
prevents visualizations of parts of the eye as:
 The angle of anterior chamber (Fig)
 The periphery of the retina
NB: this problem is overcome by applying a contact lens
made of a material with a higher refractive than the eye
and fitting space between the eye and lens with saline to
destroy cornea-air refracting surface and allowing
visualization of
 The anterior chamber angle by gonioscopy. (fig1 &2)
 The retinal periphery by a 3-mirror contact lens (fig3)
angle of anterior chamber

33. 1) Visualization of angle of AC by goniolens
2) Koeppe goniolens
3) Goldmann three or four mirror lens

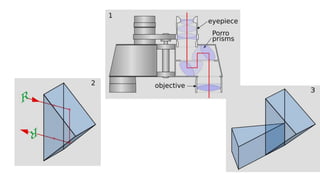
34. 2. Forms of prisms used in ophthalmic instruments.
As reflectors of light (with total internal reflection within the prism 1) right angled prism with
deviation 90°, 2) right angled prism with deviation 180° [Porro prism], 3) two right angled
prisms, 4) Dove prism

36. 3.To get the refractive index n of a medium by measuring the critical angle c:
n = sin i/sin r = sin c/sin 90°
4. Fiber optics (fig)
 Optical fiber consists of a core of transparent solid material (as glass or
plastic) with a high refractive index surrounded by a coating with a lower
refractive index.
 The high-index to low-index interface between the core and the glass tube is
the cause of repeated total internal reflection of a ray.
 Parallel bundles of these fibers are called ‘coherent fiber optic bundle’ which
transposes the entire incidence face to the emergence face as in several
electro-optical devices including computer output terminals.
5.Internal reflection explains the secondary rainbow formation

37. A simplified drawing of a surgical endoscope. The first
lens forms a real image at one end of a bundle of optical
fibers. The light is transmitted through the bundle, and is
finally magnified by the eyepiece. Example same given
as periscope.
Total internal reflection in a fiber-optic cable

39. References
 Optics by Benjamin Crowell (light and matter series)
 Textbook of Clinical Ophthalmic Optics
 Optics and Refraction Outline by David G. Hunter, MD, PhD
 The Eye and Visual Optical Instruments by G. Smith and David A.
Atchison
 Refraction, Dispensing Optics and Ophthalmic Procedures by Ashwani
Kumar Ghai, MS
 Borish’s Clinical Refraction by William J. Benjamin

40. THANK YOU FOR YOUR ATTENTION