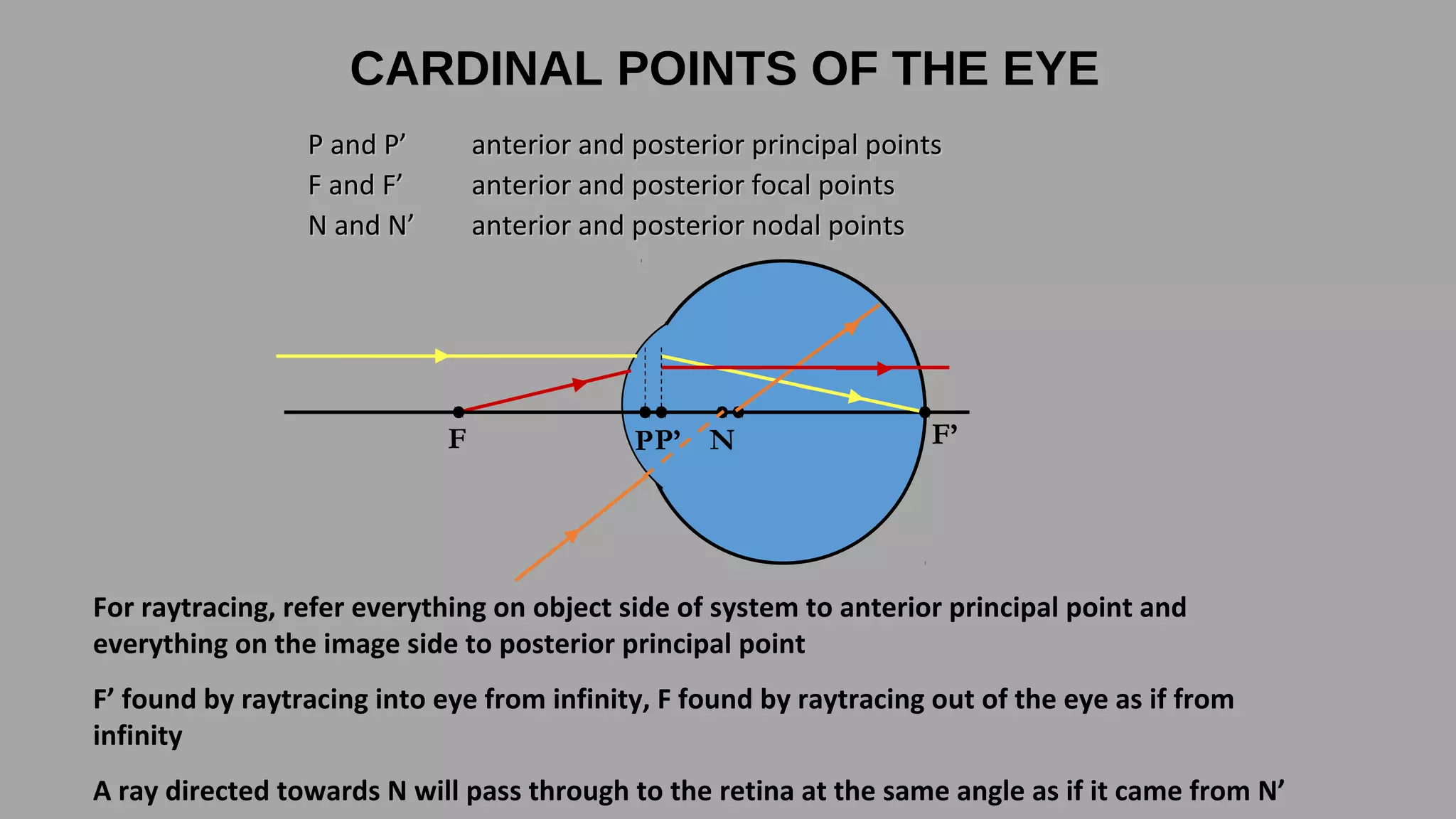
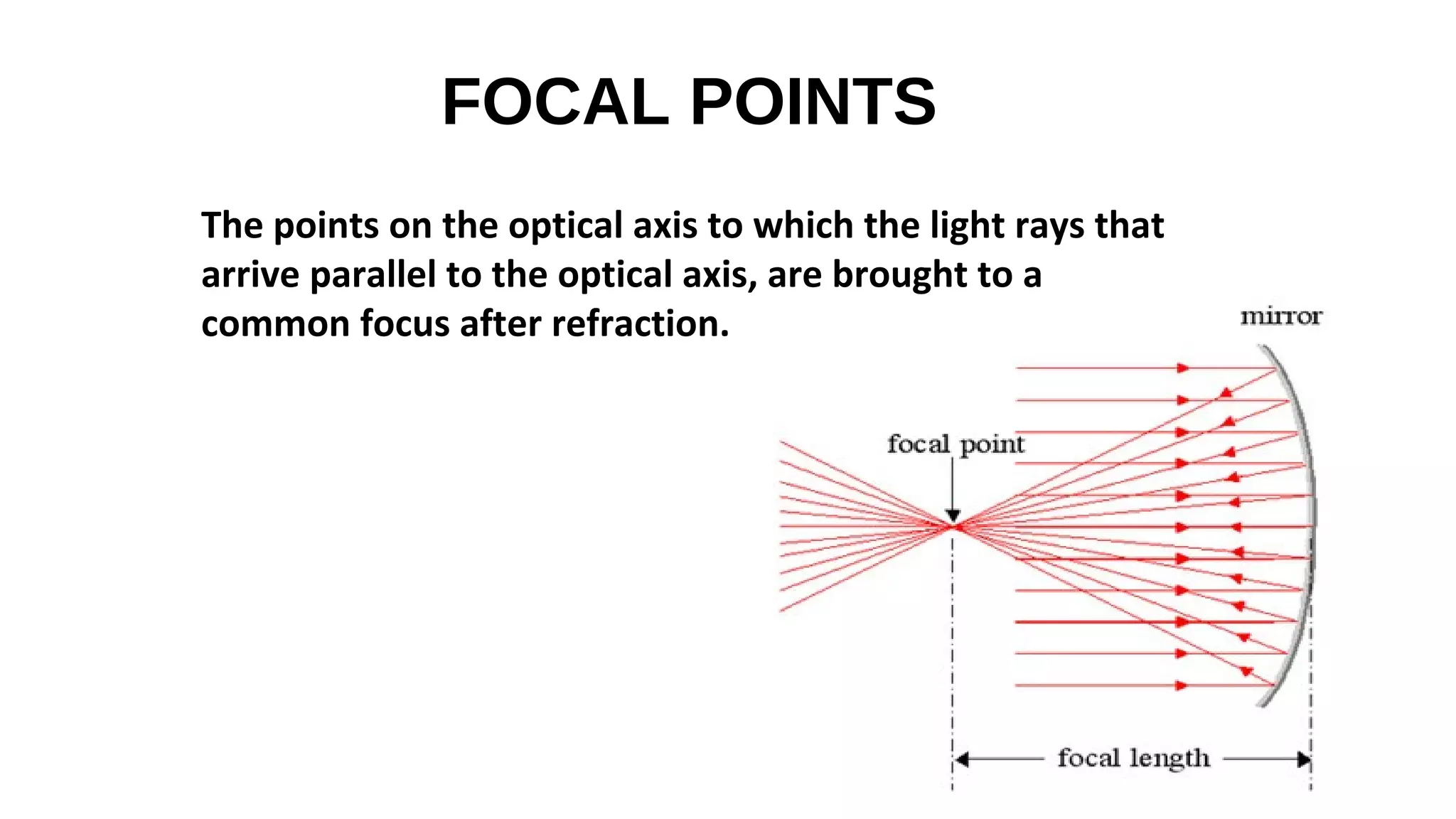
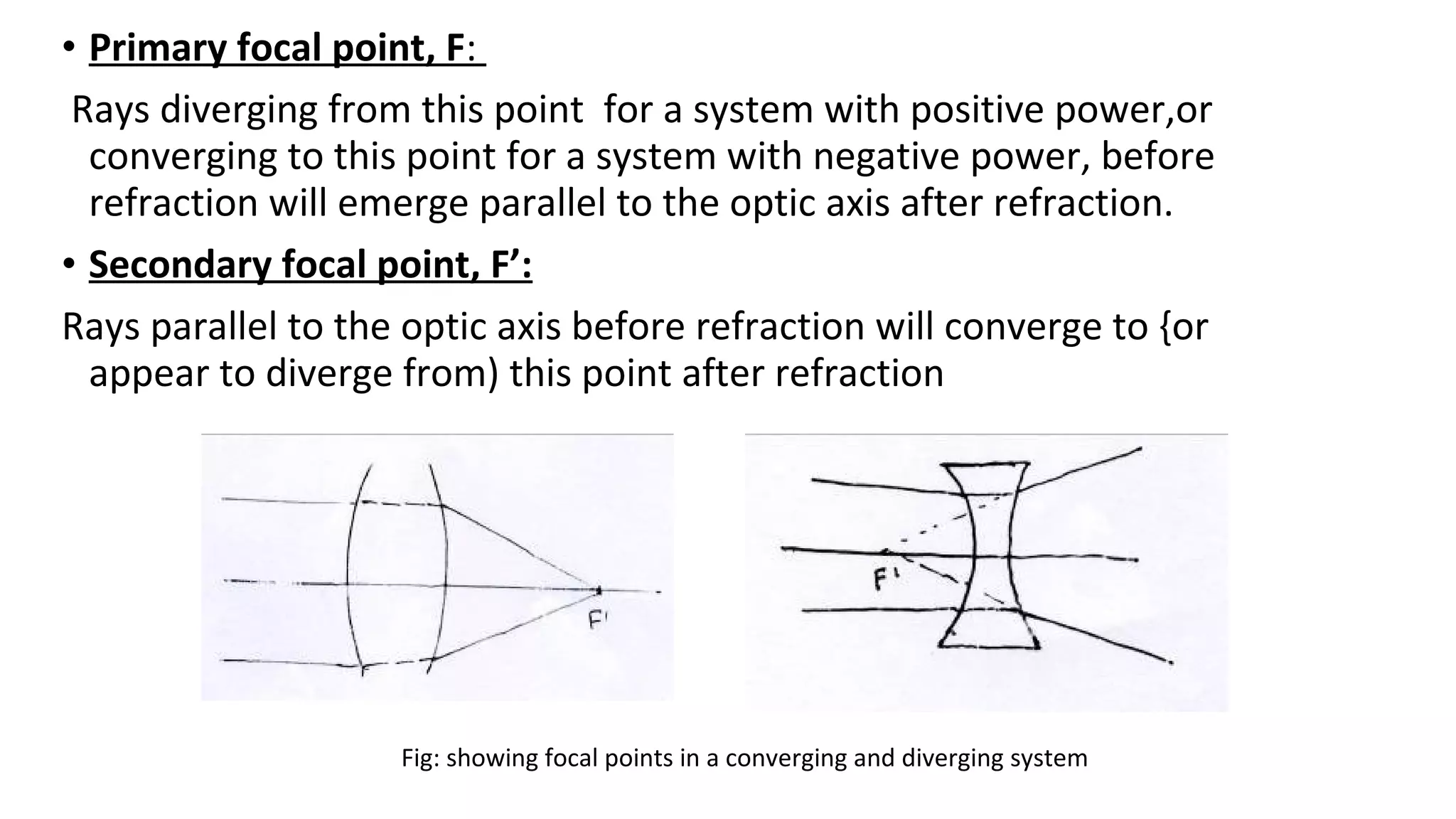
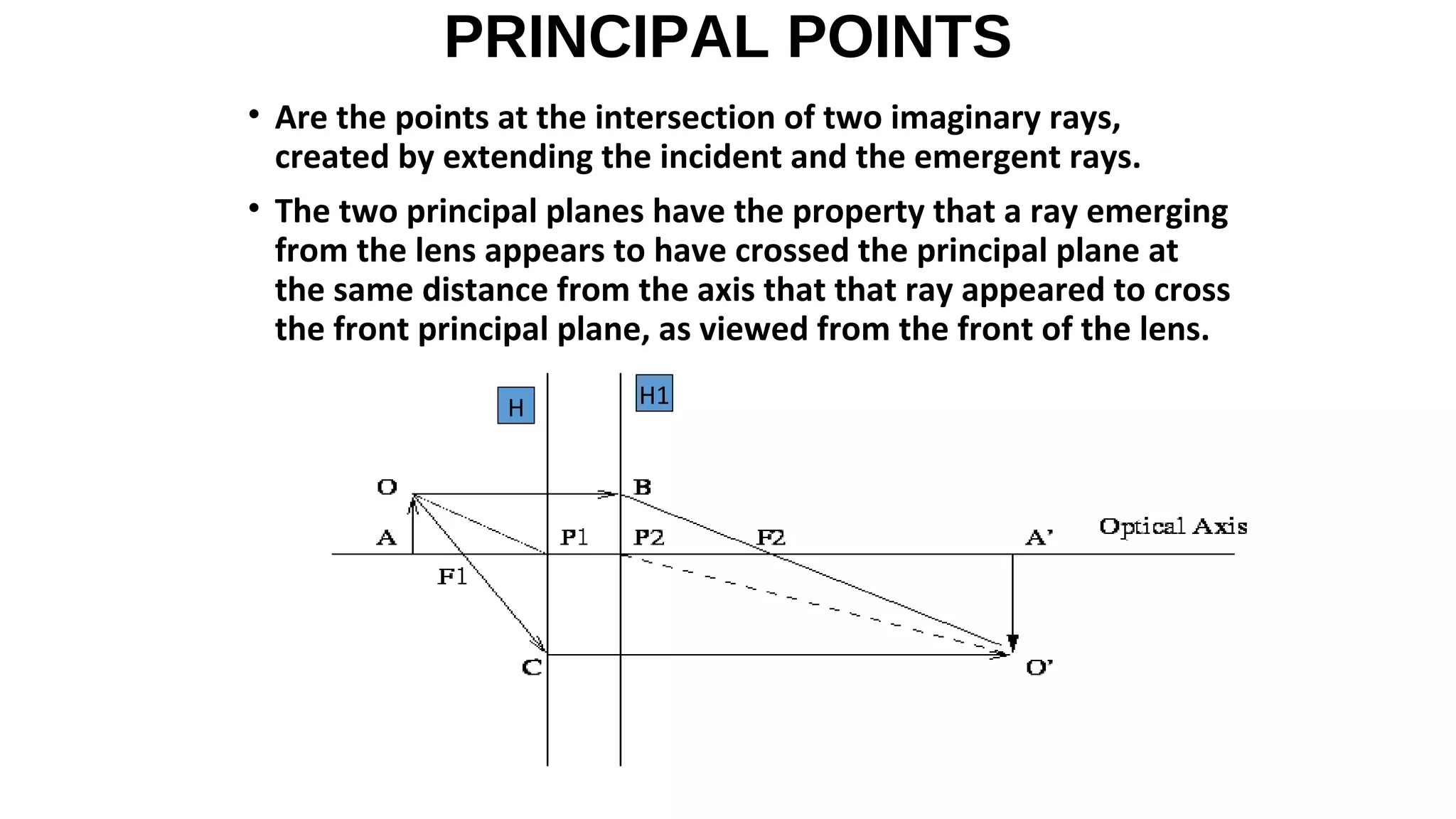
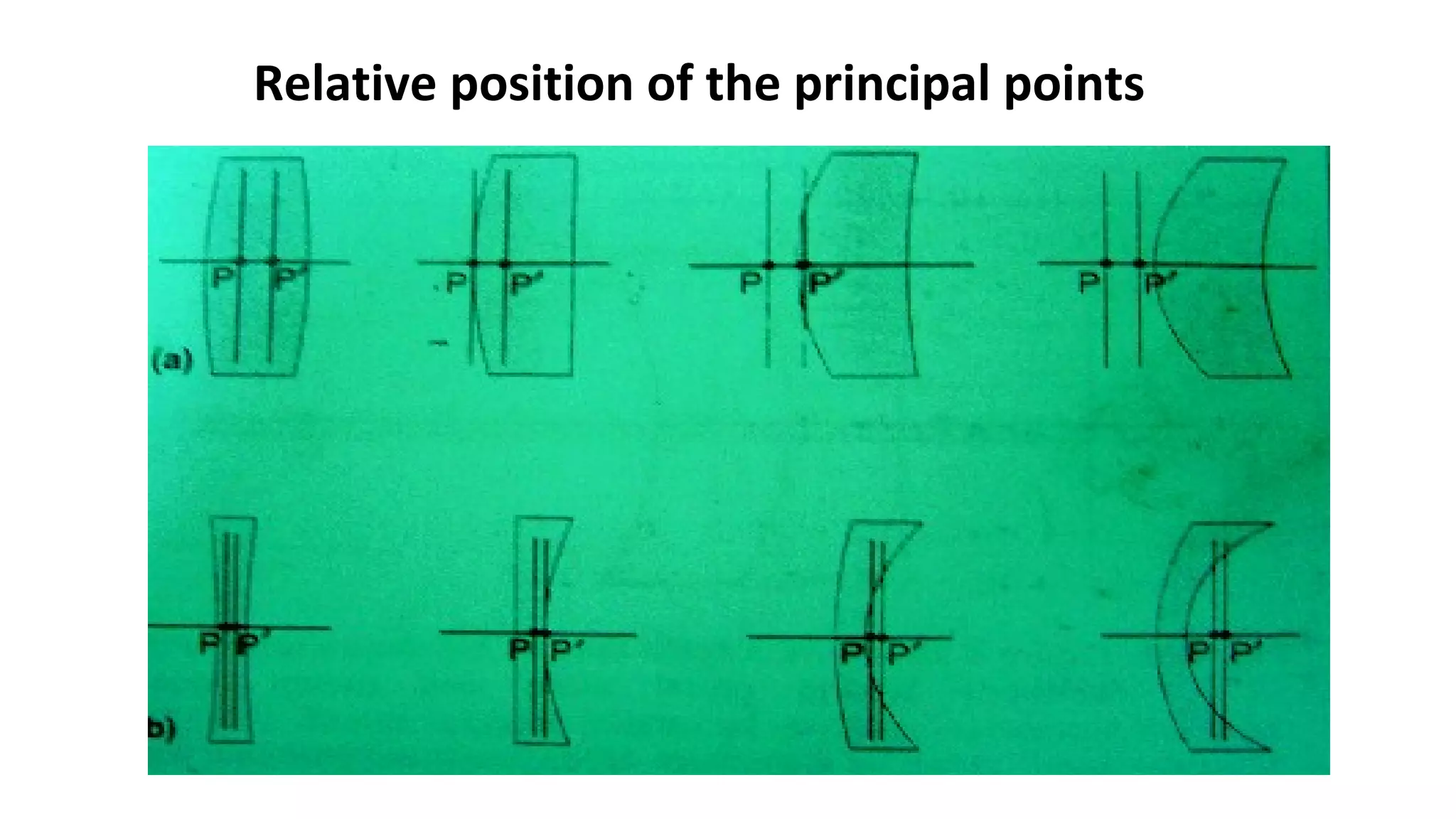
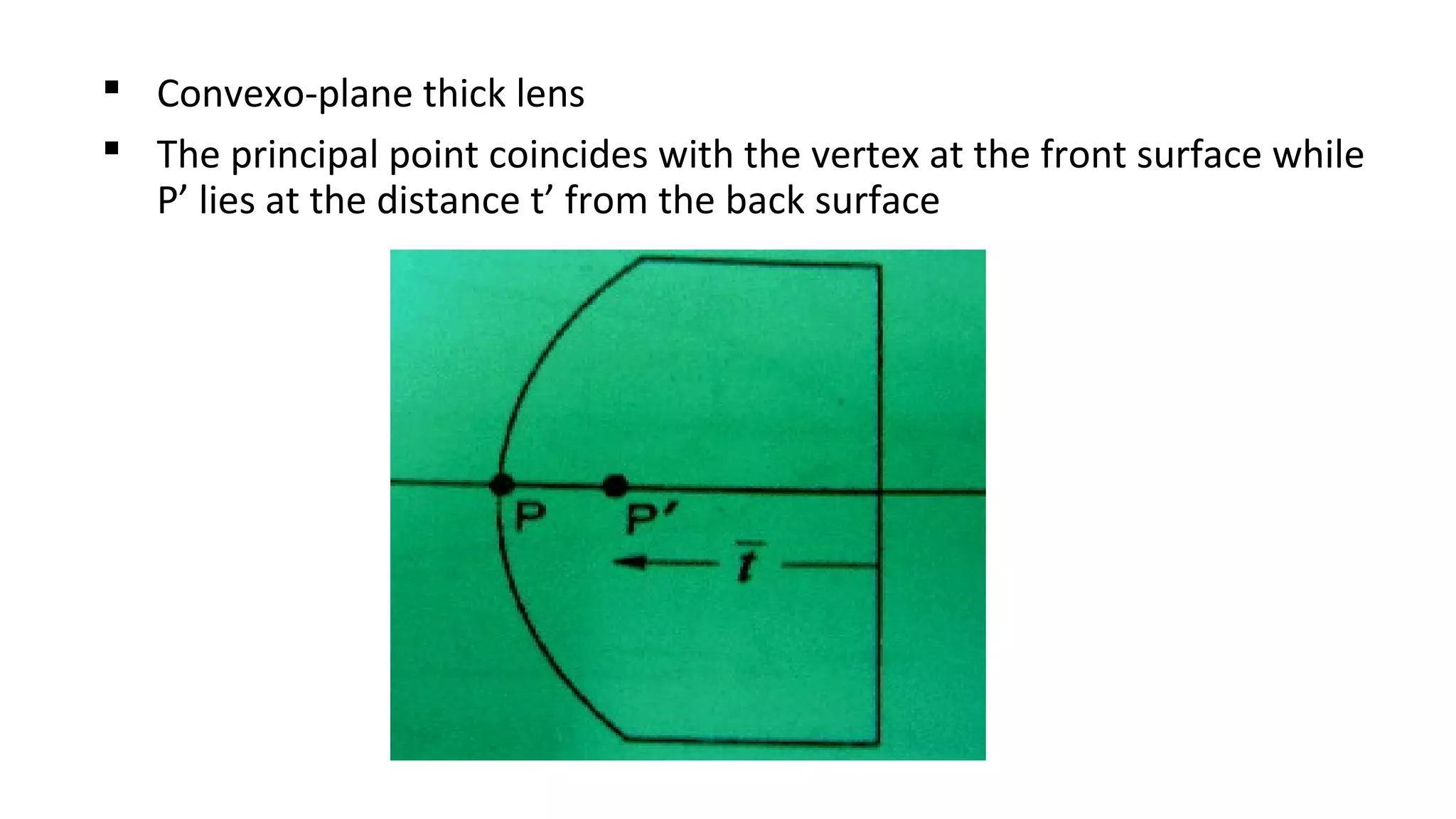
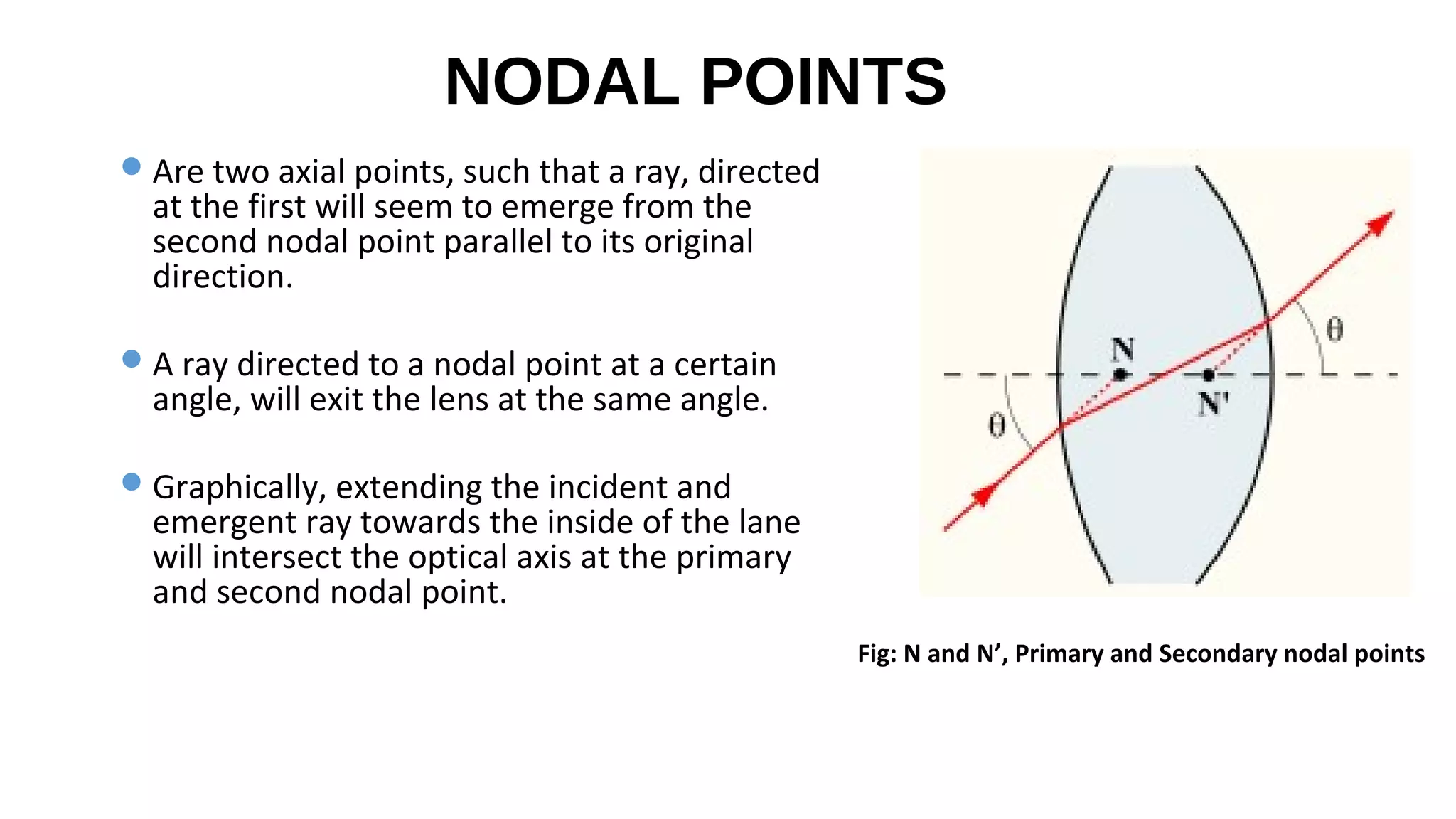
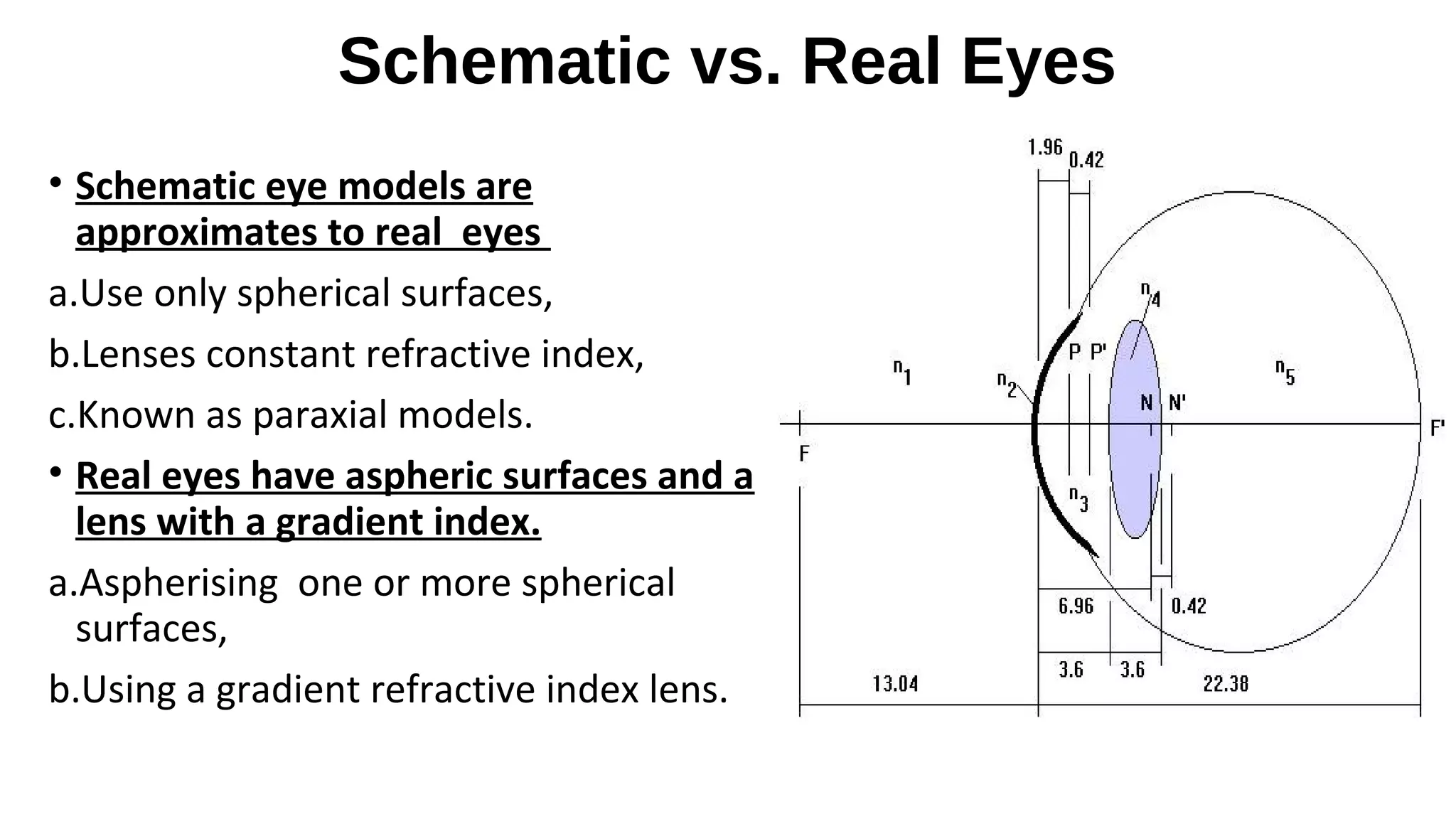
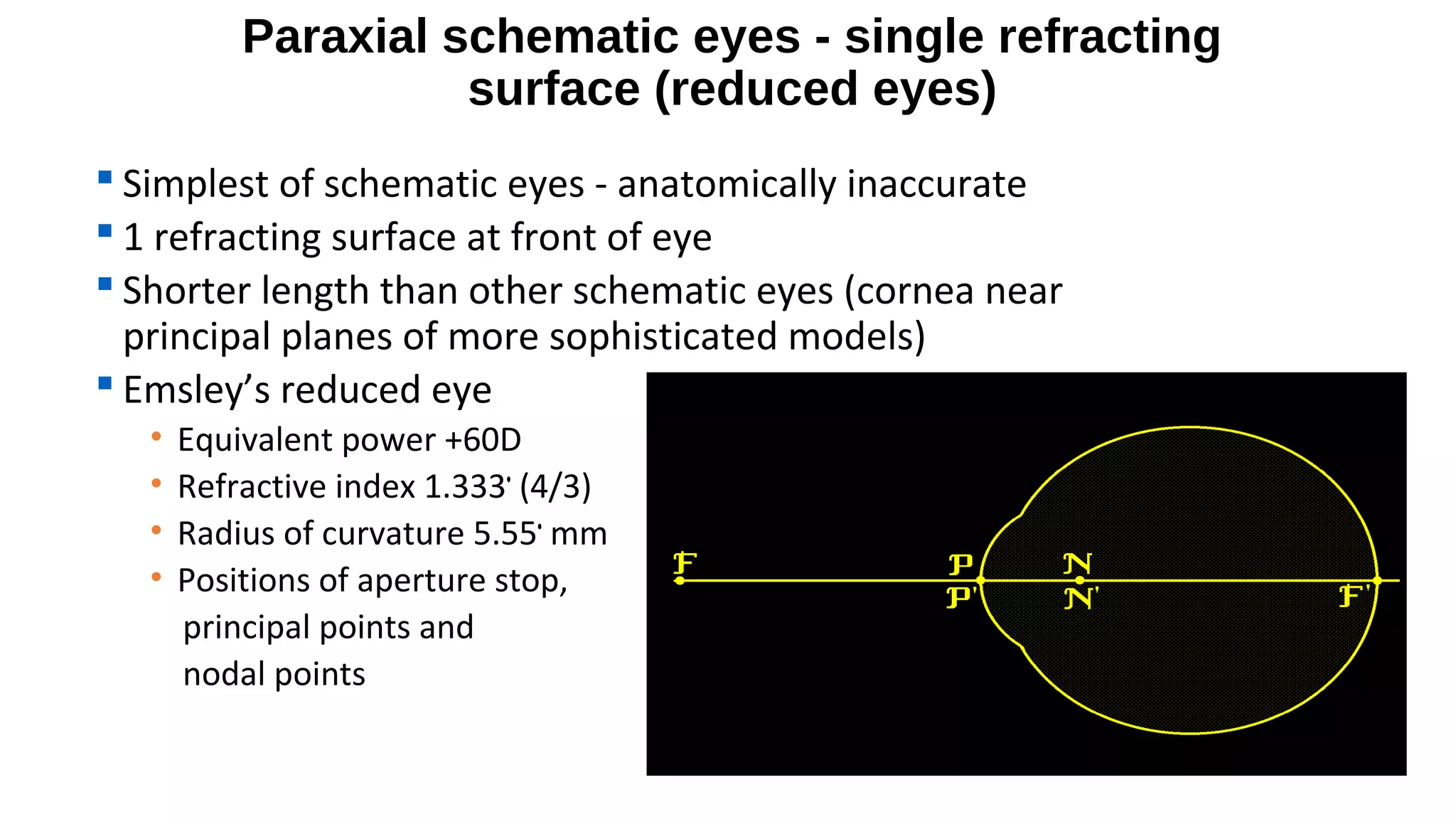
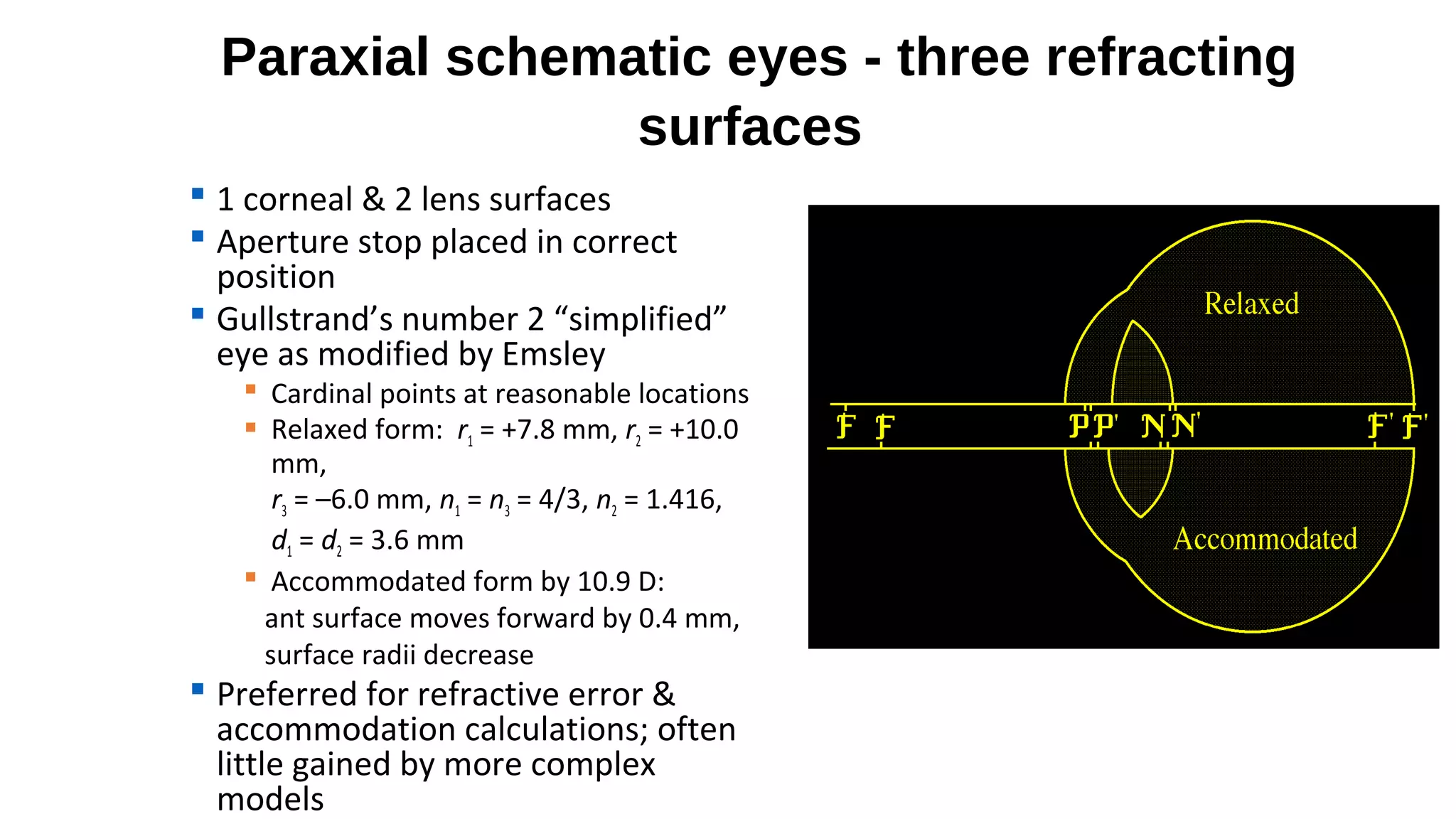
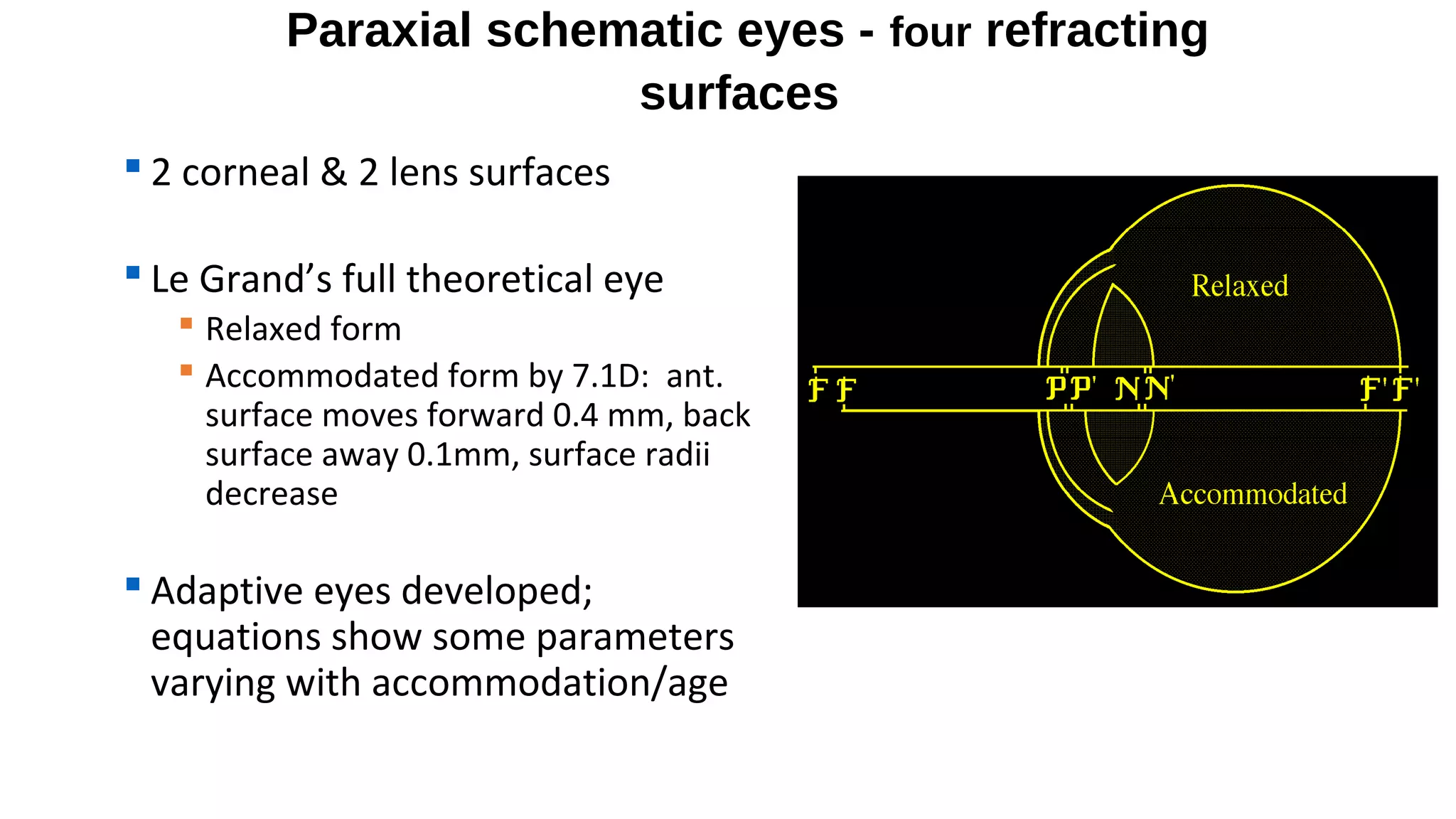
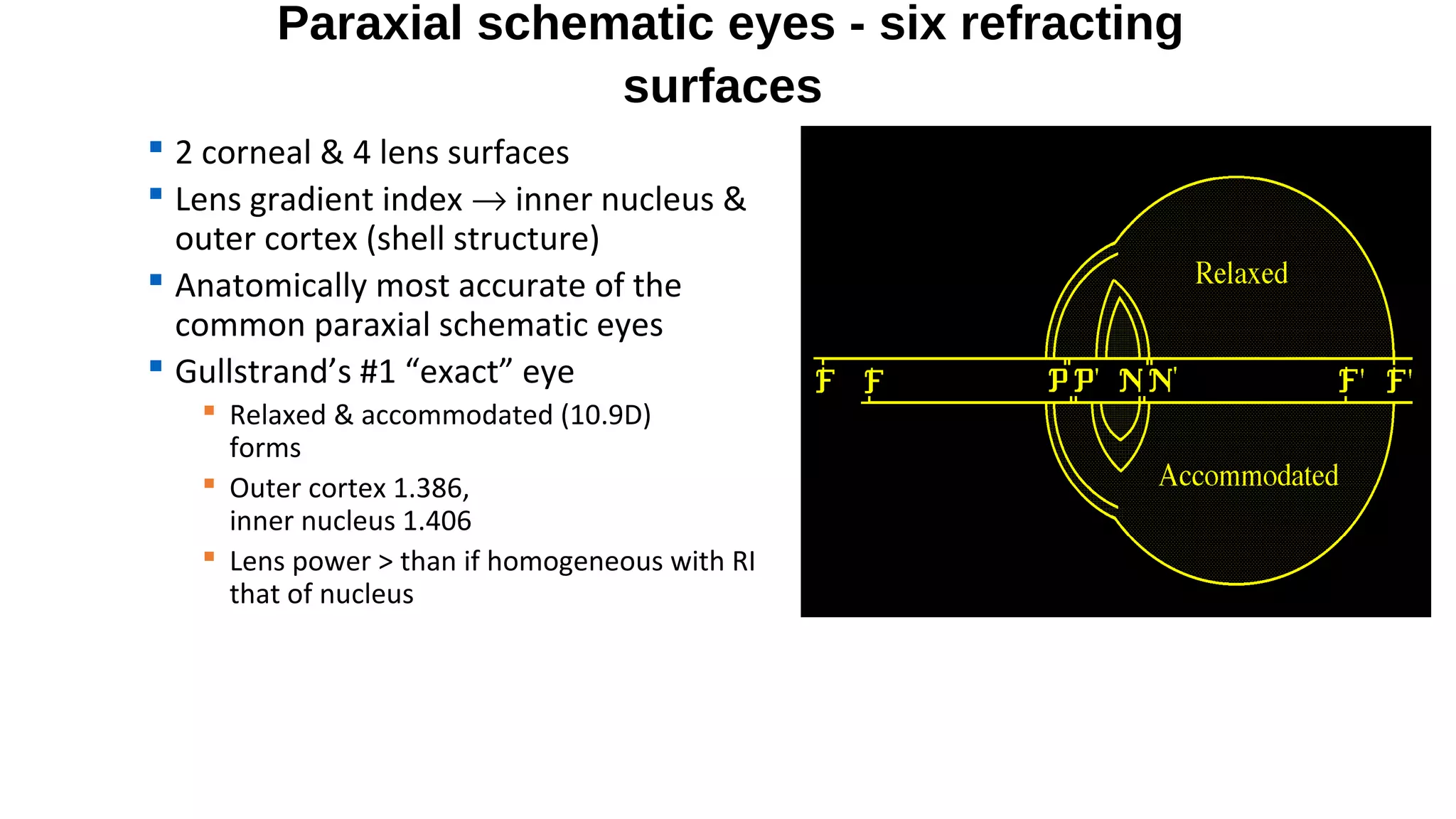
This document discusses schematic eyes and cardinal points. It provides an overview of different types of schematic eyes including paraxial and finite models. Paraxial eyes are simplified models useful for basic calculations while finite eyes are more accurate by including aspheric surfaces. The document also describes the six cardinal points - focal points, principal points, and nodal points - which define the optical properties and image formation of an eye. It explains how the locations of these points change under different conditions like aphakia. In summary, the document provides a comprehensive overview of schematic eye models and the important cardinal points used to analyze the optical performance of the eye.

1. Schematic eye and Cardinal Points
Mohammad Arman Bin Aziz
Optometry Officer
ICO, CU
February 24, 2014

2.  Simplified optical models of real eyes


Constructional parameters generally means of population distributions
Vary in their complexity and thus suitability for applications
 Used for
 Retinal image size
 Retinal light levels
 Refractive errors resulting from variations in eye dimensions
 Power of intraocular lenses to replace cataractous lens
 Aberrations & retinal image quality with/without optical or surgical intervention

3. Schematic vs. Real Eyes
• Schematic eye models are
approximates to real eyes
a.Use only spherical surfaces,
b.Lenses constant refractive index,
c.Known as paraxial models.
• Real eyes have aspheric surfaces and a
lens with a gradient index.
a.Aspherising one or more spherical
surfaces,
b.Using a gradient refractive index lens.

4. Types according to Inventors
Types of this eyes:
1.Listing’s reduced eye
2.Emsely’s reduced eye
3.Donder’s reduced eye
4.Bennett and Rabbett’s reduced eye

5. TYPES OF SCHEMATIC EYES - paraxial
schematic eyes
• Models simplified, only useful in the paraxial region
• Aberrations much greater than those of real eyes
• Refracting surfaces co-axial & spherical
• Visual axis coincides with optical axis
• Refractive Index of lens is constant (usually)

6. Paraxial schematic eyes - single refracting
surface (reduced eyes)
 Simplest of schematic eyes - anatomically inaccurate
 1 refracting surface at front of eye
 Shorter length than other schematic eyes (cornea near
principal planes of more sophisticated models)
 Emsley’s reduced eye
•
•
•
•
Equivalent power +60D
Refractive index 1.333• (4/3)
Radius of curvature 5.55• mm
Positions of aperture stop,
principal points and
nodal points

7. Applications
• Serve as a frame work for studying the Gaussian properties for e.g.
Equivalent power and positions of the cardinal point
• Calculation of retinal image sizes
• Magnifications
• Retinal illumination
• Entrance and exit pupil positions and diameters
• Surface reflections and some of the causes and effects of refractive
errors
• Effect of accommodation on the above quantities
• Paraxial models accurately predict chromatic aberration

8. Limitations
• Approximation of real eyes that are Constructed with rotationally
symmetric spherical surfaces
• Refractive index assumed to be constant
• Construction parameters mean of many individual values called as
average eye
• Very poor predictors of monocular aberrations

9. Paraxial schematic eyes - three refracting
surfaces
 1 corneal & 2 lens surfaces
 Aperture stop placed in correct
position
 Gullstrand’s number 2 “simplified”
eye as modified by Emsley
 Cardinal points at reasonable locations
 Relaxed form: r1 = +7.8 mm, r2 = +10.0
mm,
r3 = –6.0 mm, n1 = n3 = 4/3, n2 = 1.416,
d1 = d2 = 3.6 mm
 Accommodated form by 10.9 D:
ant surface moves forward by 0.4 mm,
surface radii decrease
 Preferred for refractive error &
accommodation calculations; often
little gained by more complex
models

10. Paraxial schematic eyes - four refracting
surfaces
 2 corneal & 2 lens surfaces
 Le Grand’s full theoretical eye
 Relaxed form
 Accommodated form by 7.1D: ant.
surface moves forward 0.4 mm, back
surface away 0.1mm, surface radii
decrease
 Adaptive eyes developed;
equations show some parameters
varying with accommodation/age

11. Paraxial schematic eyes - six refracting
surfaces
 2 corneal & 4 lens surfaces
 Lens gradient index → inner nucleus &
outer cortex (shell structure)
 Anatomically most accurate of the
common paraxial schematic eyes
 Gullstrand’s #1 “exact” eye
 Relaxed & accommodated (10.9D)
forms
 Outer cortex 1.386,
inner nucleus 1.406
 Lens power > than if homogeneous with RI
that of nucleus

12. Paraxial schematic eye - four refracting
surfaces with gradient index lens
 Shell structure Gullstrand exact eye
→ gradient index
 Ray tracing through gradient index
media more complex than single
index media
•
•
RI distribution
n(r) = n0 + n1r2 + n2r4 + ...
r = relative distance from centre
Power due to gradient index
F = -2t/b2(2/3n1 + 3/5n2 + ...)
t = lens thickness, b = lens semidiameter

13. TYPES of SCHEMATIC EYES - Finite schematic
eyes
 Developed to be accurate outside the paraxial region
 Better aberration predictions at large apertures and fields of view
 Development paraxial schematic eyes, using having aspheric surfaces
 Curved retinas → determination of off-axis aberrations
 Chromatic aberration determined from dispersion values of different
media
 Customisation to model individual eyes

14. Applications
Framework for calculations of
Retinal image sizes
Magnifications
Retinal illumination
Entrance and exit pupil positions and diameters
Aberration analysis
Light level distribution at the retina
As a model for the design of visual optical instruments
Analysis of intra ocular lenses

15. Finite schematic eyes – conicoid
asphericity
• Simplest type of aspheric surface is conicoid
• Conic section rotated about its axis of
symmetry.
y
Q < -1
Q = -1
c[(x2 + y2) + z2 (1 + Q)] – 2z = 0
-1 < Q < 0
c is the vertex curvature of the surface and Q is
conic constant
Q=0
z
Q < –1 hyperboloid
Q = –1 paraboloid
–1 < Q < 0 flattening ellipsoid (prolate)
Q = 0 sphere
Q > 0 steepening ellipsoid (oblate)
x
Q>0

16. Cardinal Points
• Are a set of six points situated on the optical axis which are defined in
such a way so as to facilitate the image formation by the lens system.
Every Optical systems has 6 CARDINAL POINTS
•
•
•
1. Focal PointsPrimary & Secondary
2. Principal Points- Primary & Secondary
3. Nodal PointsPrimary & Secondary
*These points are defined following the tradition that light is always supposed to travel
from left to right in optical system.

17. CARDINAL POINTS OF THE EYE
P and P’
F and F’
N and N’
anterior and posterior principal points
anterior and posterior focal points
anterior and posterior nodal points
F
P P’ N
F’
For raytracing, refer everything on object side of system to anterior principal point and
everything on the image side to posterior principal point
F’ found by raytracing into eye from infinity, F found by raytracing out of the eye as if from
infinity
A ray directed towards N will pass through to the retina at the same angle as if it came from N’

18. Importance
• we can find out various information about the image of an object
produced by an optical system.
• Information about;
 Size
 Location of image

19. FOCAL POINTS
The points on the optical axis to which the light rays that
arrive parallel to the optical axis, are brought to a
common focus after refraction.

20. • Primary focal point, F:
Rays diverging from this point for a system with positive power,or
converging to this point for a system with negative power, before
refraction will emerge parallel to the optic axis after refraction.
• Secondary focal point, F’:
Rays parallel to the optic axis before refraction will converge to {or
appear to diverge from) this point after refraction
Fig: showing focal points in a converging and diverging system

21. PRINCIPAL POINTS
• Are the points at the intersection of two imaginary rays,
created by extending the incident and the emergent rays.
• The two principal planes have the property that a ray emerging
from the lens appears to have crossed the principal plane at
the same distance from the axis that that ray appeared to cross
the front principal plane, as viewed from the front of the lens.
H
H1

22. PRINCIPAL POINTS AND PLANES
 A perpendicular drawn to the optical axis from any other principal points
cross the optical axis at the main principal point.
 The principal planes are the planes normal to the optical axis,
intersecting the principal points on the optical axis.
 For all incident rays having equal angles of incidence have their
principal points on the same plane.
 All distances related to optical systems are measured from principal
planes.

23. Relative position of the principal points

24.  Convexo-plane thick lens
 The principal point coincides with the vertex at the front surface while
P’ lies at the distance t’ from the back surface

25. NODAL POINTS
 Are two axial points, such that a ray, directed
at the first will seem to emerge from the
second nodal point parallel to its original
direction.
 A ray directed to a nodal point at a certain
angle, will exit the lens at the same angle.
 Graphically, extending the incident and
emergent ray towards the inside of the lane
will intersect the optical axis at the primary
and second nodal point.
Fig: N and N’, Primary and Secondary nodal points

26. Cont.…
 When an optical axis is bounded on both sides by the same medium then
the nodal points coincide with the principal points.
For differing indices for converging system the nodal points move towards
the higher index side and converse occurs for diverging system.
 When an optical system has equal curvature and RI on both sides, it will
have a single principal point and a single nodal point for one set of incident
ray and they will coincide.

27. CHANGES IN CARDINAL
POINTS
IN APHAKIA
Eye becomes highly hyperopic
Power of eye reduces from +60D to +44D
Anterior focal point becomes23.2mm in front of cornea
Posterior focal point is about 31mm behind the cornea i.e. 7mm behind the
eyeball
Nodal points are very near to each other and are located about 7.75mm behind
the anterior surface of cornea
The two principal points are almost at anterior surface of cornea

28. Important to Know
• Nodal points in myopic eye is further away from the retina.
• So, the image formed will be appreciably larger than it would be in
the emmetropic eye and in spectacle corrected eye.
• The concept of schematic eye is strongly dependent on cardinal
points.
• In PSCC-hyperopic shift
• In nuclear sclerosis-myopic shift

29. References
 Atchison DA, Smith G (2000). Optics of the human eye, chapters 2, 3,
5, and 16, and Appendix 3. Butterworth-Heinemann, Oxford.
 Rabbetts RB (2007). Bennett and Rabbetts’ clinical visual optics,
 Lecture of Dr David A Atchison, School of Optometry & Vision Science,
Institute of Health and Biomedical Innovation, Queensland University
of Technology, Brisbane, Australia
 Lecture of Mr Mezbah Uddin, lecturer, ICO, CU
 Lecture of Mr Jewel Das Gupta, Optometry Instructor, ICO, CU