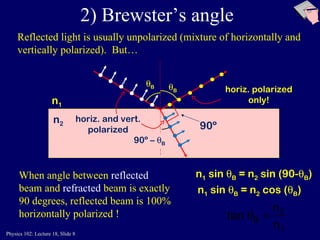
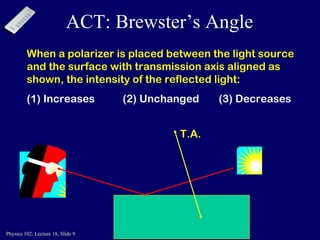
The document summarizes key concepts from a Physics 102 lecture on optics, including Snell's law, total internal reflection, Brewster's angle, dispersion, and lenses. Snell's law describes how light bends when passing from one medium to another. Total internal reflection occurs when light hits the boundary between two media at an angle greater than the critical angle. Brewster's angle is when the reflected light is completely polarized. Dispersion is why prisms separate white light into a rainbow spectrum. Lenses use refraction to converge or diverge light rays depending on their shape.

1. Snell’s Law, Total Internal Reflection, Brewster’s Angle, Dispersion, Lenses Physics 102: Lecture 18

3. Demo: Snell’s Law n 2 n 1 > n 2 When light travels from one medium to another the speed changes v=c/n, but the frequency is constant. So the light bends: n 1 sin(  1 )= n 2 sin(  2 ) n 1 > n 2   2 >  1 Light bent away from normal as it goes in medium with lower n  1  2  r incident reflected refracted

4. 1) Total Internal Reflection normal n 2 n 1 > n 2 Snell’s Law: n 1 sin(  1 )= n 2 sin(  2 ) (n 1 > n 2   2 >  1 )  1 = sin -1 (n 2 /n 1 ) then  2 = 90 Light incident at a larger angle will only have reflection (  i =  r ) For water/air: n 1 =1.33, n 2 =1  1 = sin -1 (n 2 /n 1 ) = 48.8 0 “ critical angle”  1  2  i >  c  r  c

5. Fiber Optics Telecommunications Arthoscopy Laser surgery Total Internal Reflection only works if n outside < n inside At each contact w/ the glass air interface, if the light hits at greater than the critical angle, it undergoes total internal reflection and stays in the fiber. n inside n outside

6. Can the person standing on the edge of the pool be prevented from seeing the light by total internal reflection ? 1) Yes 2) No Preflight 18.1

8. 2) Brewster’s angle When angle between reflected beam and refracted beam is exactly 90 degrees, reflected beam is 100% horizontally polarized ! Reflected light is usually unpolarized (mixture of horizontally and vertically polarized). But… n 1 sin  B = n 2 sin (90-  B ) n 1 sin  B = n 2 cos (  B ) horiz. and vert. polarized  B  B 90º –  B 90º horiz. polarized only! n 1 n 2

9. ACT: Brewster’s Angle When a polarizer is placed between the light source and the surface with transmission axis aligned as shown, the intensity of the reflected light: (1) Increases (2) Unchanged (3) Decreases T.A.

11. 3) Dispersion Prism Blue light gets deflected more n blue > n red The index of refraction n depends on color! In glass: n blue = 1.53 n red = 1.52 White light  blue <  red  red  i  blue

12. Skier sees blue coming up from the bottom (1) , and red coming down from the top (2) of the rainbow. Rainbow: Preflight 18.5 Wow look at the variation in index of refraction! Which is red ? Which is blue ? Blue light is deflected more!

13. LIKE SO! In second rainbow pattern is reversed

14. 4) Lenses Focal point determined by geometry and Snell’s Law : n 1 sin(  1 ) = n 2 sin(  2 ) Converging lens: – Rays parallel to P.A. converge on focal point Diverging lens: – Rays parallel to P.A. diverge as if emerging from focal point behind lens Larger n 2 /n 1 = more bending, shorter focal length. Smaller n 2 /n 1 = less bending, longer focal length. n 1 = n 2 => No Bending, f = infinity F         “ Plano-convex” “ Plano-concave” P.A. F P.A.

15. Converging & Diverging Lenses Converging lens: – Rays parallel to P.A. converge on focal point Diverging lens: – Rays parallel to P.A. diverge as if emerging from focal point behind lens “ Plano-convex” “ Plano-concave” Converging = fat in the middle Diverging = thin in the middle “ Double concave” “ Double convex” = = = = “ Convex-concave” “ Concave-convex”

16. 1) Rays parallel to principal axis pass through focal point. 2) Rays through center of lens are not refracted. 3) Rays through F emerge parallel to principal axis. Converging Lens Principal Rays F F Object P.A. Image is: real, inverted and enlarged (in this case). Example Image Key assumptions: • monochromatic light incident on a thin lens. • rays are all “near” the principal axis.

18. 3 Cases for Converging Lenses This could be used in a camera. Big object on small film Inverted Reduced Real Past 2F This could be used as a projector. Small slide on big screen Inverted Enlarged Real Between F & 2F This is a magnifying glass Upright Enlarged Virtual Inside F Object Image Image Object Image Object

20. 1) Rays parallel to principal axis pass through focal point. 2) Rays through center of lens are not refracted. 3) Rays toward F emerge parallel to principal axis. Diverging Lens Principal Rays F F Object P.A. Only 1 case for diverging lens : Image is always virtual, upright, and reduced . Example Image