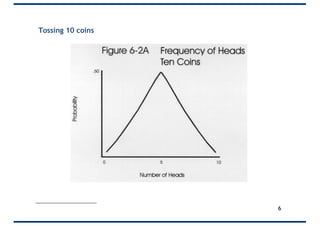
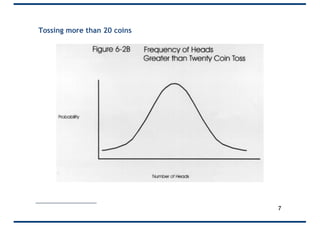
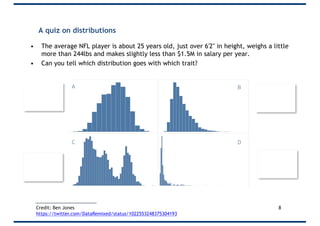
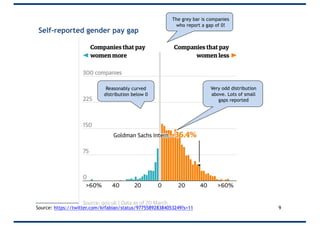
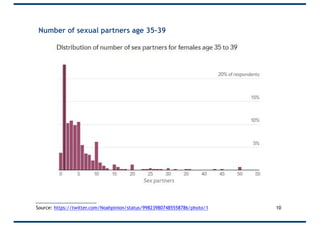
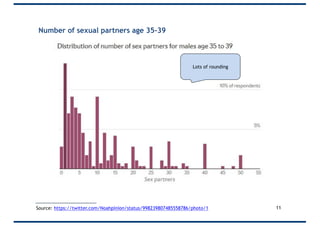
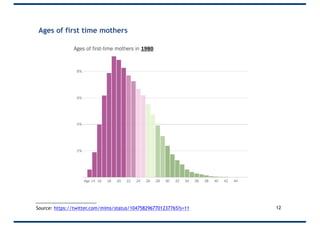
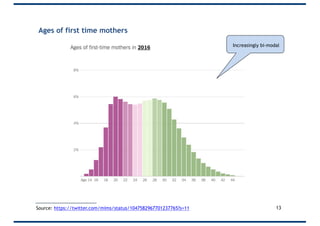
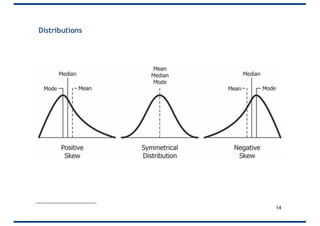
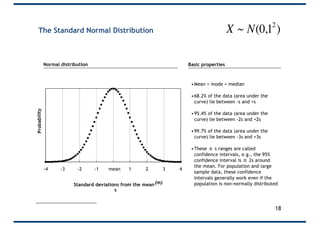
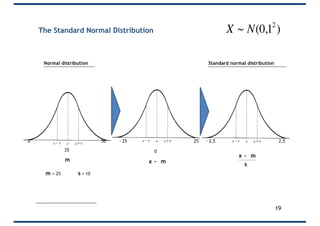
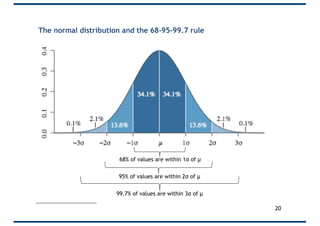
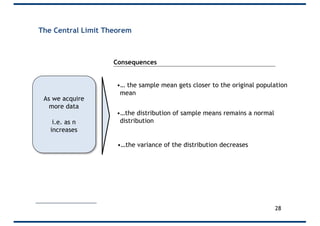
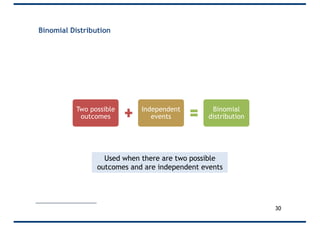
The document covers probability distributions, focusing on normal, binomial, and Poisson distributions, along with the central limit theorem. It explains how to read and apply these distributions in practical scenarios, including examples involving coin tossing and customer arrivals. Students are expected to develop an understanding of these concepts and their applications in statistics.







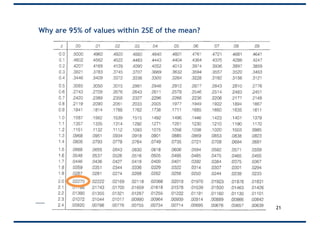






![The Binomial Distribution: Example
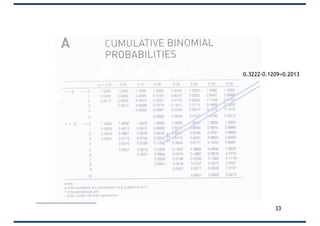
• If one-in-five items coming off a machine are
defective, what is the probability of three or more
defectives in a sample of 10 items?
• For P(0,10) = 1*(0.200)*(0.8010) = 0.1073
• For P(1,10) = 10*(0.201)*(0.809)
• For P(2,10) = 45*(0.202)*(0.808)
• P(>=3) = 1 – [P(2)+P(1)+P(0)]
= 1 – 0.678
= 32.2%
n = 10
p = 0.20
q = 0.80
r = the number of times
that the event occurs
p, n, and r can be put into a Binomial Table
34
€
P(r,n) =
n
r
"
#
$
%
&
'pr
q(n−r)](https://image.slidesharecdn.com/probabilitydistributionss-181220094651/85/Probability-Distributions-34-320.jpg)











![The Binomial Distribution: Example
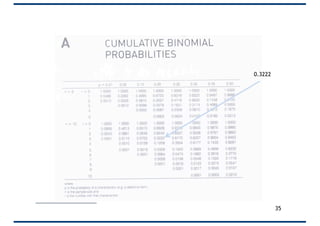
• If one-in-five items coming off a machine are
defective, what is the probability of three or more
defectives in a sample of 10 items?
• For P(0,10) = 1*(0.200)*(0.8010) = 0.1073
• For P(1,10) = 10*(0.201)*(0.809)
• For P(2,10) = 45*(0.202)*(0.808)
• P(>=3) = 1 – [P(2)+P(1)+P(0)]
= 1 – 0.678
= 32.2%
n = 10
p = 0.20
q = 0.80
r = the number of times
that the event occurs
p, n, and r can be put into a Binomial Table
50
€
P(r,n) =
n
r
"
#
$
%
&
'pr
q(n−r)](https://image.slidesharecdn.com/probabilitydistributionss-181220094651/85/Probability-Distributions-50-320.jpg)