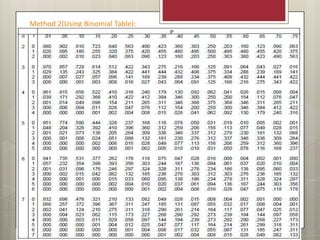
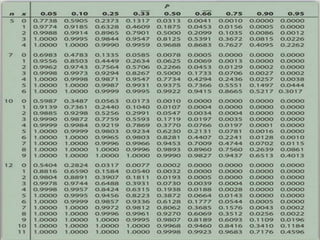
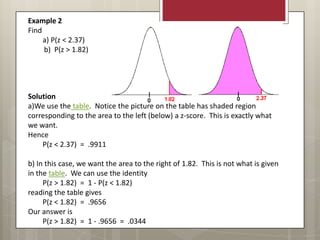
The document provides an overview of statistical distributions, including the binomial, normal, and Poisson distributions, detailing their characteristics and applications. It outlines the conditions for binomial experiments, compares binomial to normal distributions, and offers examples of calculating probabilities with these distributions. Additionally, it presents methods for using z-scores in normal distributions and the Poisson formula for discrete events.

1. Binomial
Distribution and
Applications

2. Binomial Probability Distribution
Is the binomial distribution is a continuous
distribution?Why?
Notation: X ~ B(n,p)
There are 4 conditions need to be satisfied for a
binomial experiment:
1. There is a fixed number of n trials carried out.
2. The outcome of a given trial is either a
“success”
or “failure”.
3. The probability of success (p) remains constant
from trial to trial.
4. The trials are independent, the outcome of a
trial is not affected by the outcome of any
other trial.

3. Comparison between binomial and normal
distributions

4. Binomial Distribution
If X ~ B(n, p), then
where
successof
trials.insuccessesofnumberr
11!and10!also,1...)2()1(!
yprobabilitP
n
nnnn
.,...,1,0r)1(
)!(!
!
)1()( npp
rnr
n
ppcrXP rnrrnr
n
r

5. Exam Question
 Ten percent of computer parts produced by a
certain supplier are defective. What is the
probability that a sample of 10 parts contains
more than 3 defective ones?

6. Solution :
 Method 1(Using Binomial Formula):

7. Method 2(Using Binomial Table):

9.  From table of binomial distribution :

10. Example 2
If X is binomially distributed with 6 trials and a
probability of success equal to ¼ at each attempt.
What is the probability of
a)exactly 4 succes.
b)at least one success.

14. Example 3
Jeremy sells a magazine which is produced in order
to raise money for homeless people. The probability
of making a sale is, independently, 0.50 for each
person he approaches. Given that he approaches 12
people, find the probability that he will make:
(a)2 or fewer sales;
(b)exactly 4 sales;
(c)more than 5 sales.

19. Normal
Distribution

20. Normal Distribution
 In general, when we gather data, we expect to see
a particular pattern to
the data, called a normal distribution. A normal
distribution is one
where the data is evenly distributed around the
mean, which when plotted as a
histogram will result in a bell curve also known as
a Gaussian distribution.

21.  thus, things tend towards the mean – the closer a
value is to the mean, the more you’ll see it; and
the number of values on
either side of the mean at any particular distance
are equal or in symmetry.

22. 

23. Z-score
 with mean and standard deviation of a set of
scores which are normally distributed, we can
standardize each "raw" score, x, by converting it
into a z score by using the following formula on
each individual score:

24. Example 1
a) Find the z-score corresponding to a raw score of 132 from a normal distribution with
mean 100 and standard deviation 15.
b) A z-score of 1.7 was found from an observation coming from a normal distribution with
mean 14 and standard deviation 3. Find the raw score.
Solution
a)We compute
132 -
z = __________ = 2.133
15
b) We have
x -
1.7 = ________
3
To solve this we just multiply both sides by the denominator 3,
(1.7)(3) = x - 14
5.1 = x - 14
x = 19.1

25. Example 2
Find
a) P(z < 2.37)
b) P(z > 1.82)
Solution
a)We use the table. Notice the picture on the table has shaded region
corresponding to the area to the left (below) a z-score. This is exactly what
we want.
Hence
P(z < 2.37) = .9911
b) In this case, we want the area to the right of 1.82. This is not what is given
in the table. We can use the identity
P(z > 1.82) = 1 - P(z < 1.82)
reading the table gives
P(z < 1.82) = .9656
Our answer is
P(z > 1.82) = 1 - .9656 = .0344

26. Example 3
Find
P(-1.18 < z < 2.1)
Solution
Once again, the table does not exactly handle this type of area. However, the area
between -1.18 and 2.1 is equal to the area to the left of 2.1 minus the area to the left
of -1.18. That is
P(-1.18 < z < 2.1) = P(z < 2.1) - P(z < -1.18)
To find P(z < 2.1) we rewrite it as P(z < 2.10) and use the table to get
P(z < 2.10) = .9821.
The table also tells us that
P(z < -1.18) = .1190
Now subtract to get
P(-1.18 < z < 2.1) = .9821 - .1190 = .8631

27. Poisson
distribution

28. Definitions
 a discrete probability distribution for the count of
events that occur randomly in a given time.
 a discrete frequency distribution which gives the
probability of a number of independent events
occurring in a fixed time.

29. Poisson distribution only apply one formula:
Where:
 X = the number of events
 λ = mean of the event per interval
Where e is the constant, Euler's number (e = 2.71828...)

30. Example:
Births rate in a hospital occur randomly at an average rate of 1.8 births
per hour.
What is the probability of observing 4 births in a given hour at the
hospital?
Assuming
X = No. of births in a given hour
i) Events occur randomly
ii) Mean rate λ = 1.8
Using the poisson formula, we cam simply calculate the distribution.
P(X = 4) =( e^-1.8)(1.8^4)/(4!)
Ans: 0.0723

31.  If the probability of an item failing is 0.001, what is the probability
of 3 failing out of a population of 2000?
Λ = n * p = 2000 * 0.001 = 2
Hence, use the Poisson formula
X = 3,
P(X = 3) =
Ans: 0.1804

32. Example:
A small life insurance company has determined that on the
average it receives 6 death claims per day. Find the probability
that the company receives at least seven death claims on a
randomly selected day.

33. Analysis method
 1st: analyse the given data.
 2nd: label the value of x, λ
 At least 7 days, means the probability must be ≥ 7. but
the value will be to the infinity. Hence, must apply the
probability rule which is
 P(X ≥ 7) = 1 – P(X ≤ 6)
 P(X ≤ 6) means that the value of x must be from 0, 1, 2,
3, 4, 5, 6.
 Total them up using Poisson, then 1 subtract the
answer.
 Ans = 0.3938

34. Example:
The number of traffic accidents that occurs on a particular
stretch of road during a month follows a Poisson distribution
with a mean of 9.4. Find the probability that less than two
accidents will occur on this stretch of road during a randomly
selected month.
P(x < 2) = P(x = 0) + P(x = 1)
Ans: 0.000860