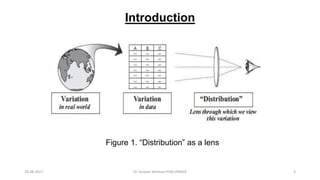
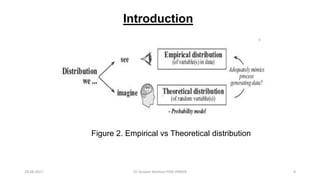
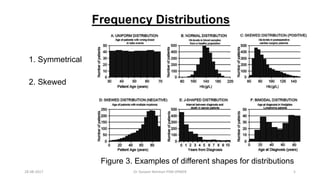
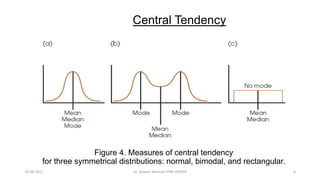
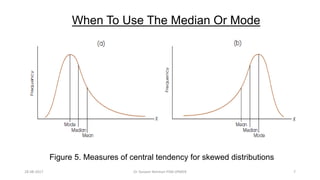
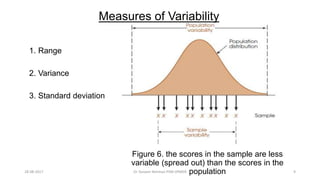
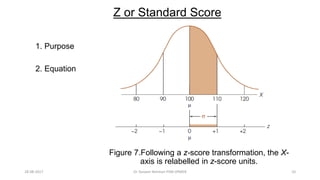
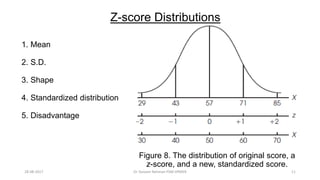
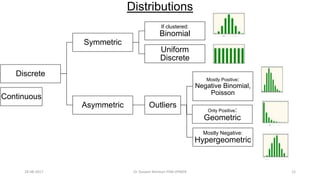
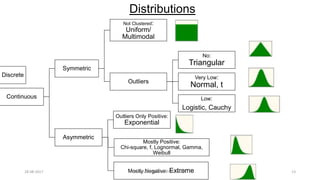
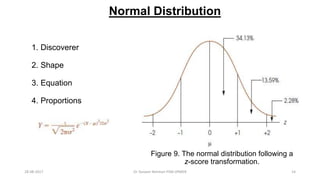
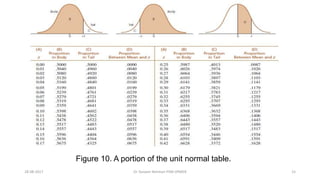
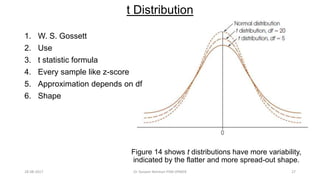
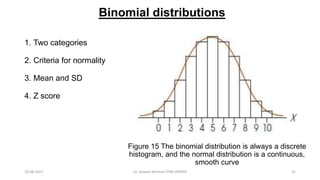
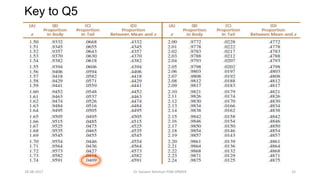
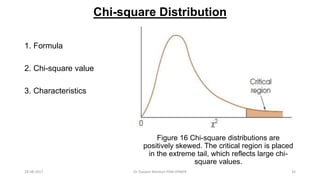
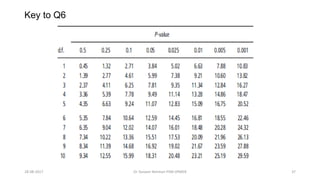
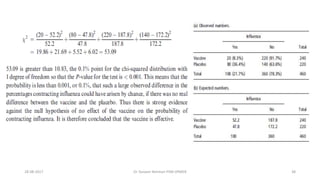
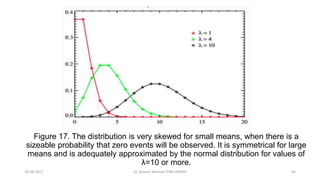
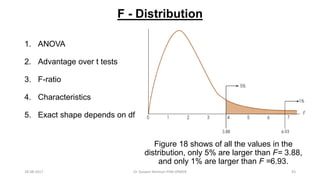
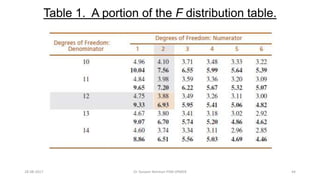
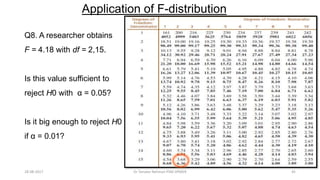
This document provides an outline and slides for a presentation on statistical distributions. It begins with an introduction to frequency distributions, measures of central tendency, variability, z-scores, and theoretical distributions. Examples of different types of distributions are shown including normal, binomial, t and chi-square distributions. The document concludes with examples of how to apply these distributions to calculate probabilities and test hypotheses related to health data.