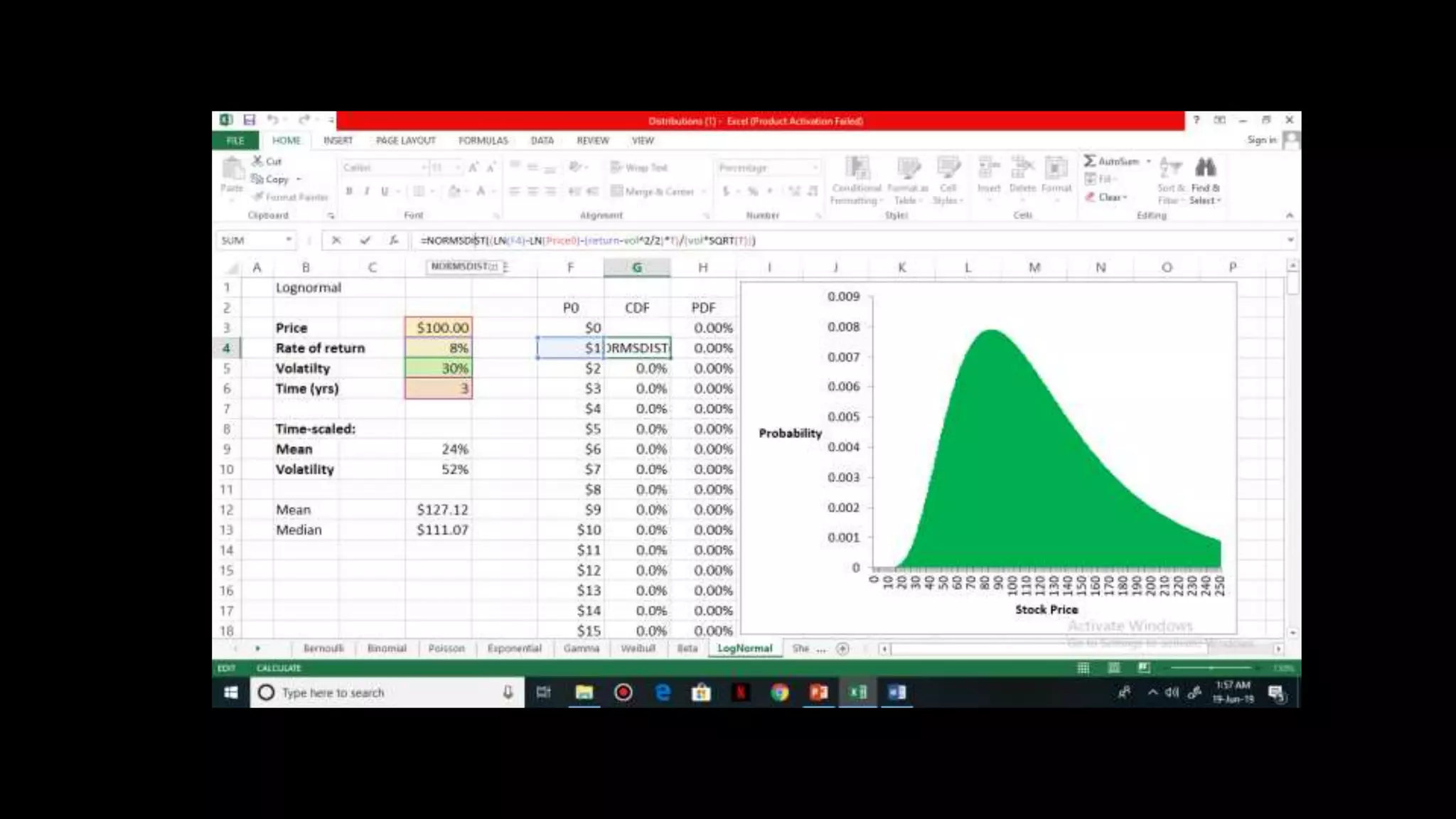
This document provides an overview of various probability distributions including discrete and continuous distributions. It defines key probability distributions such as binomial, Poisson, exponential, gamma, Weibull, beta, and log-normal distributions. Examples are given for how each distribution can be used to model different types of random variables and calculate probabilities. Applications of several distributions are demonstrated through examples in finance, healthcare, and engineering to show how the distributions can be used to model real-world scenarios.

1. Probability Distribution

2. Agenda
01
02
03
04
Meaning and Types of Distribution
Classification of Distribution
Distribution & Modelling explained
Conclusion

3. 01. Meaning and Type
Probability distribution is
nothing but a shape of
probabilities of occurrence
of various outcomes.
What is Probability
Distribution ?
Continuous
Distribution
Discrete
Distribution
Used to model random variable which has
FINITE and COUNTABLE outcome
Used to model random variable which has
INFINITE and CONTINUOUS outcome

4. 02. Classification
DISCRETE DISTRIBUTION
UniformPoisson
Bernoulli Binomial
 Used to model a
random variable
with only 2
possible
outcomes
 Used to model the
probability of ‘x’
number of
successes in ‘N’
number of trials
 Used to model the
probability of ‘x’
number of successes
in a certain period of
time given the arrival
rate of ‘lambda’
 Used to model the
outcomes with
equal probability
of occurring

5. Exponential
 Used to model
the average
waiting time
Gamma
 Used to model
the average
waiting time
given ‘alpha’
Weibull
 Used to model the
time it will take for
a machine to fail
given the failure
rate of ‘lambda’
and change in
failure rate
captured by ‘alpha’
Continuous Distribution

6. Beta
 Used to model
the recovery
rate
Normal
 Used to model
data that
follows Normal
distribution.
Eg: Returns
Log-normal
 Used to model
any data that
cannot take
negative
values, mostly,
Stock Prices
Continuous Distribution

7. 03. Distribution and Modelling
Bernoulli
Used to model a random variable with only 2
possible outcomes – Success or Failure
Parameter is ‘P’ – Probability of Success. (Success doesn’t
mean success here, it means the event defined by the
variable)
Mean = ‘P’ (Probability of success)
Variance = P * Q (Q is probability of failure i.e. 1-p)
Used in Credit Risk as a default Indicator.
Expected Loss = D.I. * LGD * EAD

8. Credit Risk – Bernoulli
EL = DI * LGD * EAD
 Bernoulli Distribution is used to find out the
Default Indicator i.e. the probability a customer will
default, while modeling the Credit Risk in Bank
 Please refer to the data given in the excel sheet.
We are using ‘P’ = 0.05 i.e. 5% of total customers
will default.
Total customers = 100
LGD = 0.60, EAD = 100
 Now, exactly which customer will default i.e. ‘DI’
can be found using Bernoulli distribution.
Here, we generate Random numbers as DI.
Function used = IF (Rand()<0.05,1,0). This means
that, if the random number generated is less than
5%, then the default will occur, which is indicated by
‘1’ and if it’s more than 5%, then default will not
occur, which is indicated by ‘0’. Now EL can be
calculated and a distribution can be plotted of the same

10. Binomial Distribution
It is a distribution of ‘N’ number of Independent and
Identically distributed Bernoulli trials
Used to find the probability of ‘x’ number of
successes in ‘N’ number of trials
Parameters of Binomial distribution are ‘N’ and ‘P’
(Probability of success)
Mean = N * P
Variance = N * P * Q ; Q = (1-p)
Probability : P(X) = N (N-1) / X! * P^X * Q^(N-X)

11. Binomial Application
 The medical equipment costs 40,000/- per day.
Charge/successful surgery = 3500/- . To cover the
cost of 40,000/- per day, we need at least 12
successful surgeries
 Probability of success in past = 0.40 i.e. ‘P’ = 0.40
We need to find out P(x> or = 12)
 We need to define 2 terms, namely, PDF and
CDF of Binomial distribution
 PDF: =Binom.dist(x,n,p,false)
 CDF =Binom.dist(x,n,p,true)
 PDF gives discrete probability at certain point
and CDF gives cumulative probability up to
certain point
 Thereafter, check the total probability of PDF
from 12 to 20 (since we need X>or = 12)
 It comes out to be 0.056 which is very low and
thus this venture should not be carried out

14. Plot of Binomial Distribution

15. Poisson Distribution
Used to find the probability of ‘x’ number of successes in a
certain period of time given an arrival rate of lambda
Parameter of Poisson distribution = Lambda
Mean = Lambda
Variance = Lambda
Probability = lambda^X * e^(-lambda) / X!
Probability : P(X) = N (N-1) / X! * P^X * Q^(N-X)

16. Poisson Application
 Suppose we have a website, wherein more than
50 log-in’s in an hour will lead to crashing of the
website
 We need to check the probability of more than 50
log-in’s in an hour i.e. P (X> 50)
 Also, an average of 20 log-in’s / hour have been
recorded i.e. lambda = 20
 Number of trials = 100
 We will find out PDF since this is a discrete
distribution.
 PDF : =poisson.dist(X,mean,false)
 Now, we need to check the PDF probability of X >
50, which is zero
 Thus, we can be rest assured that our website will
not crash

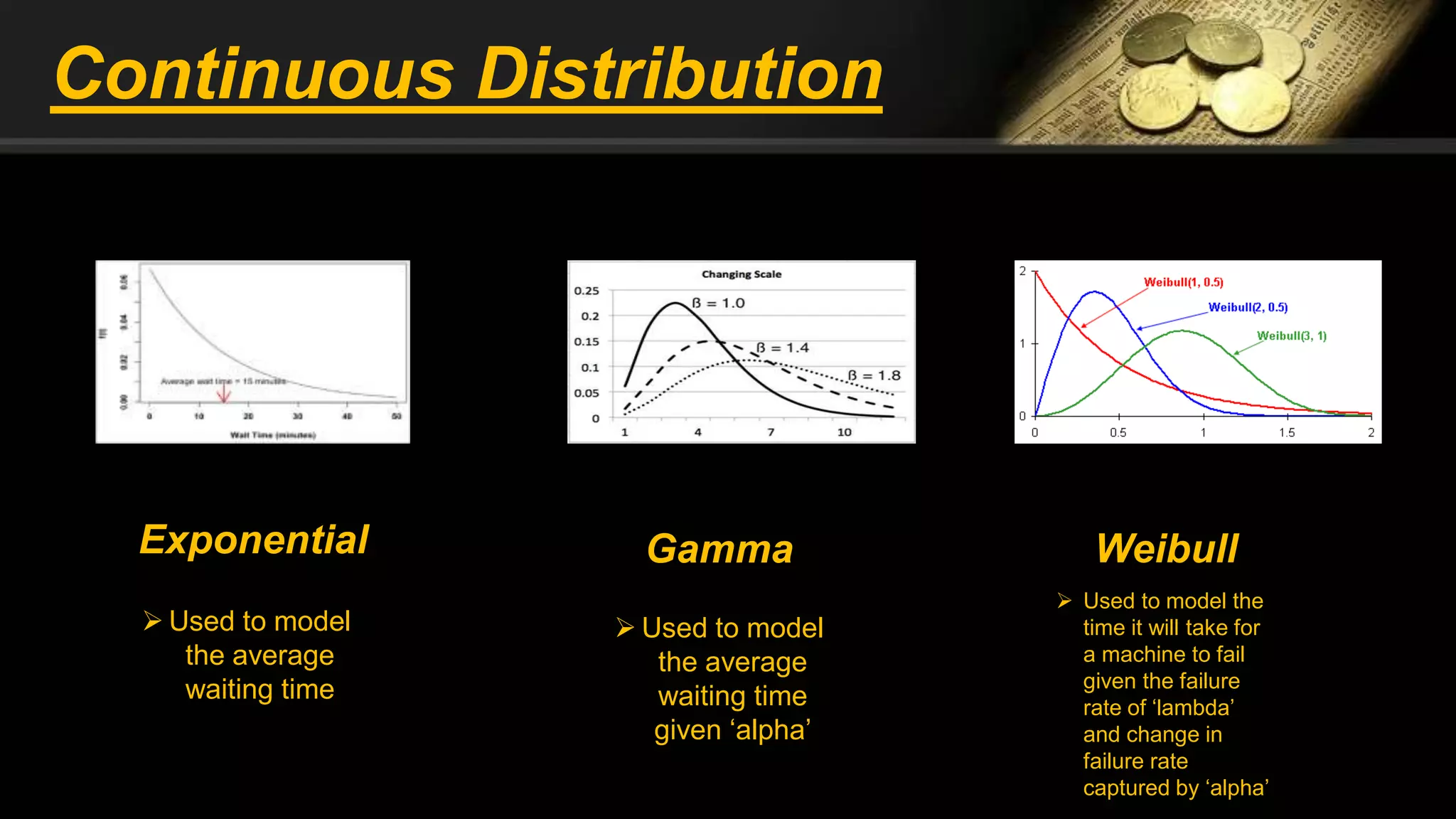
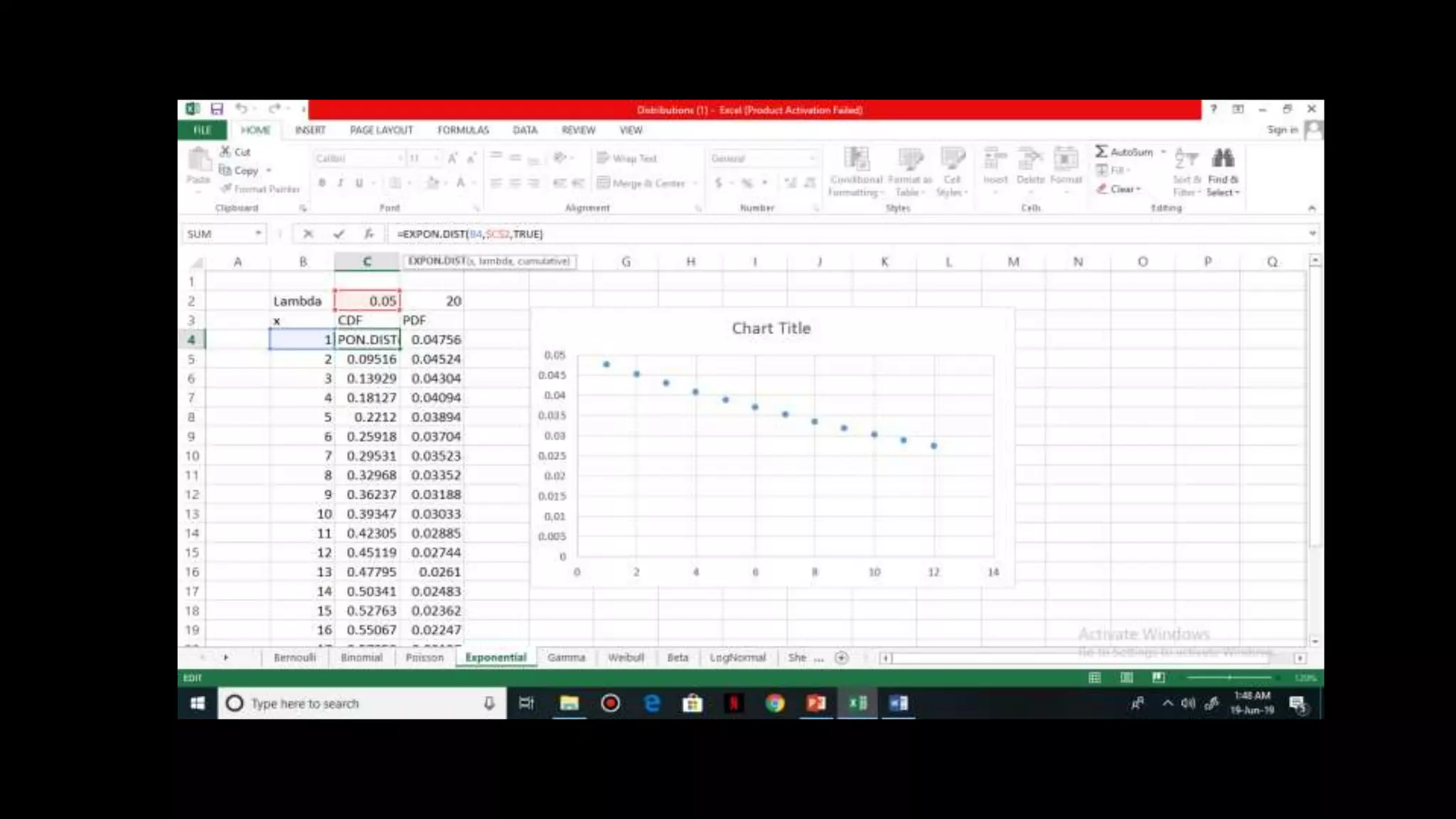
19. Exponential Distribution
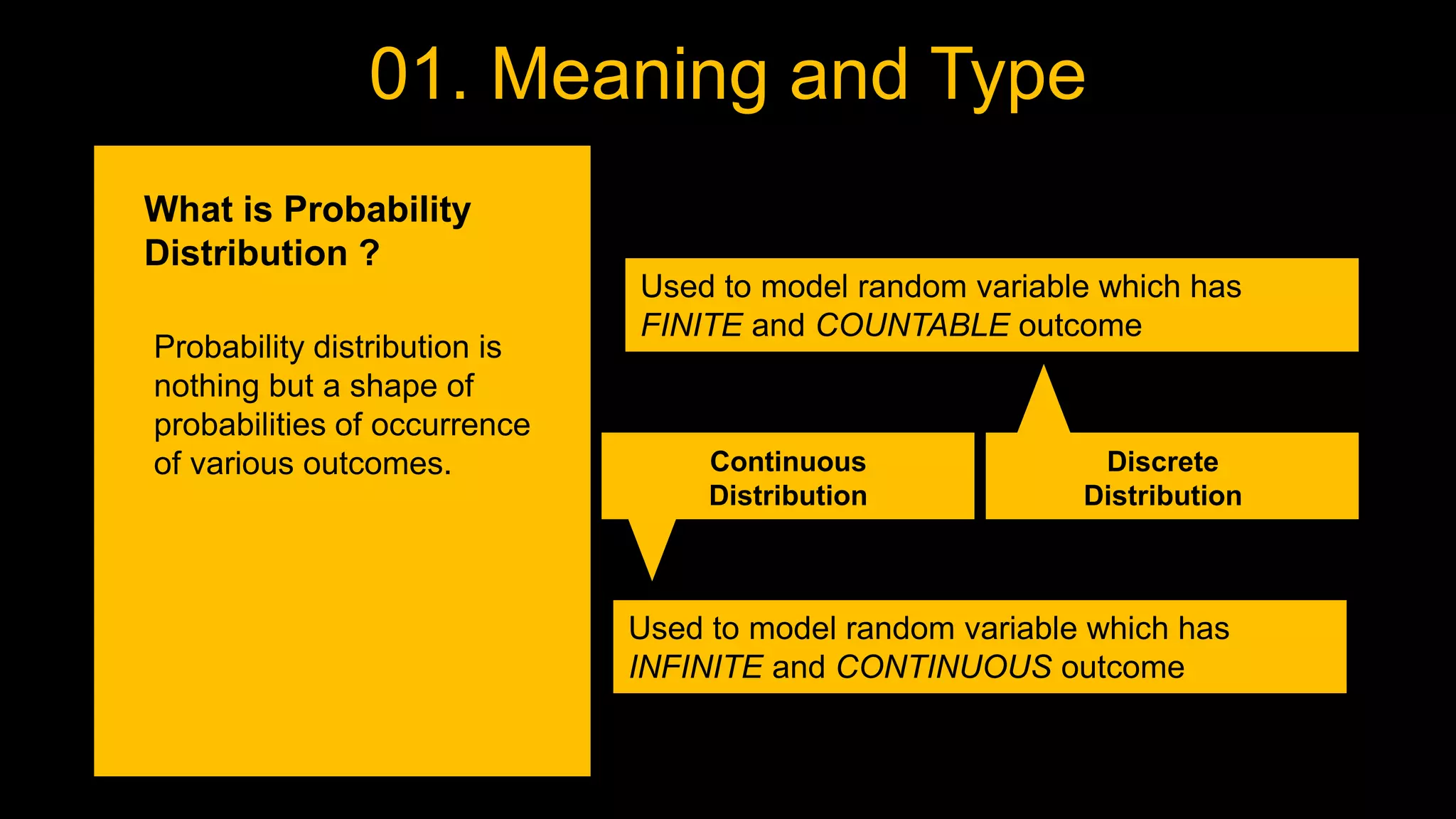
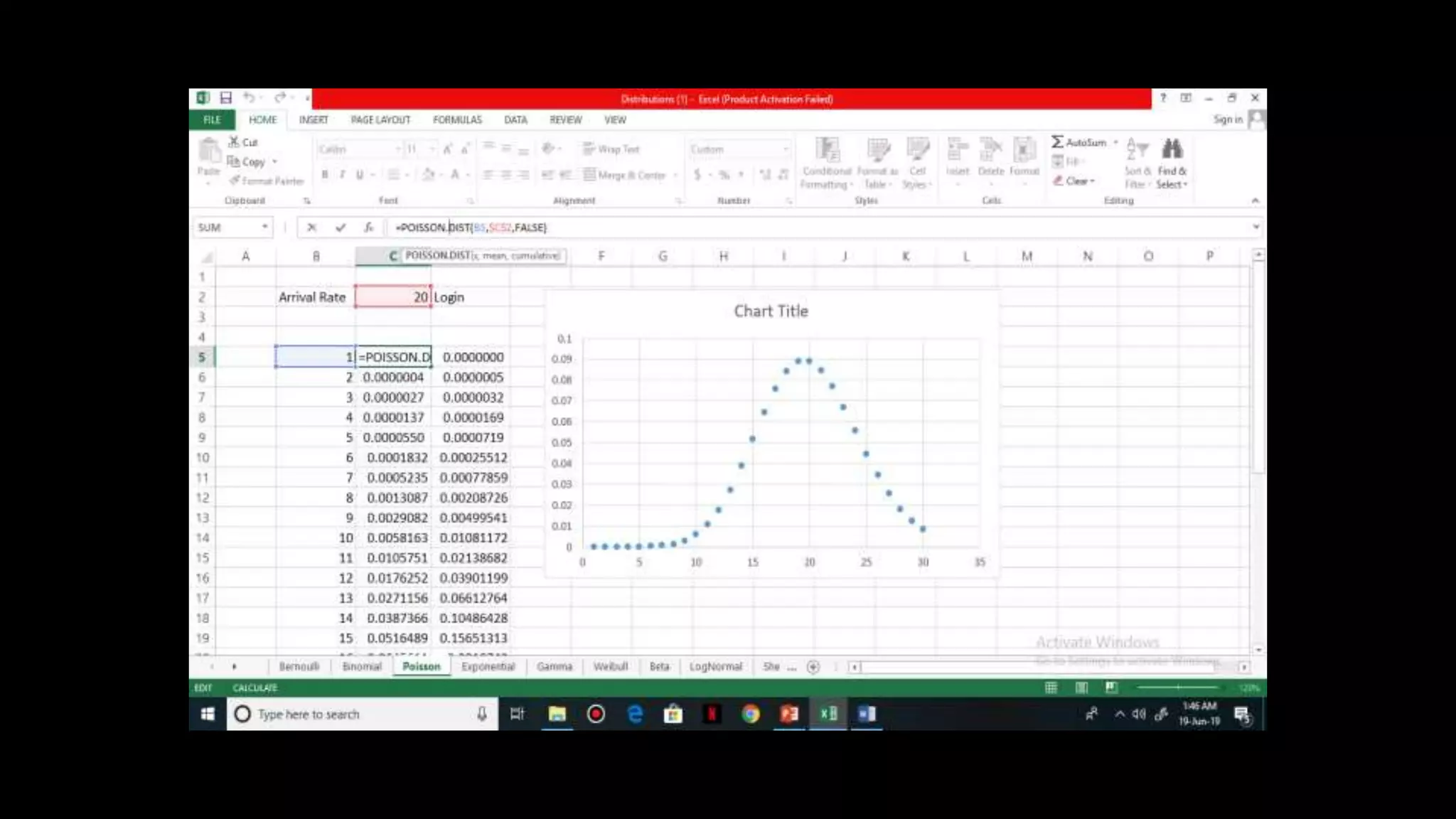
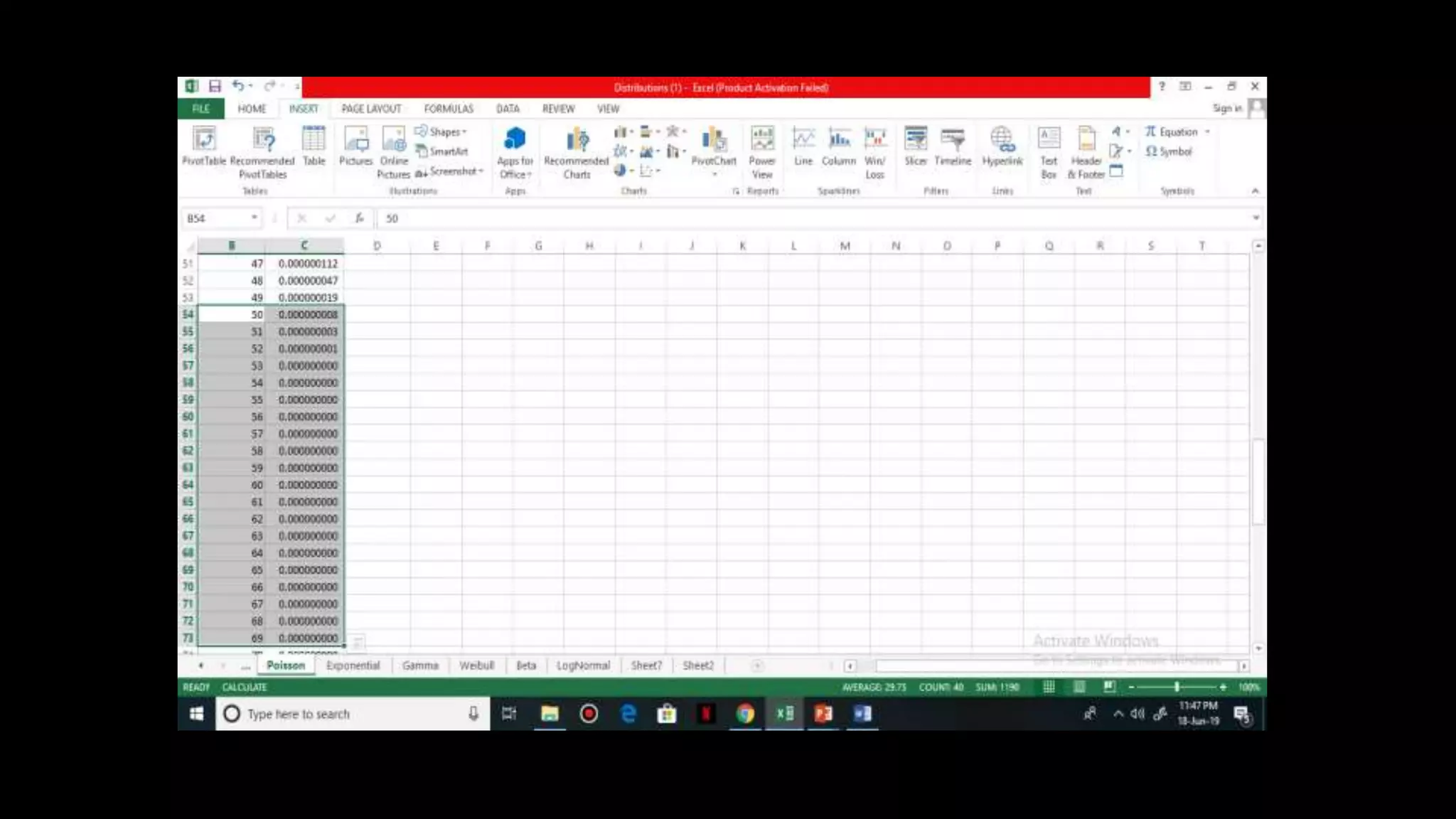
It is a continuous distribution and is used to model
average waiting time
Parameter of Exponential distribution = lambda
Mean = 1 / lambda
Variance = 1 / lambda^2
CDF , F(X) = 1 – e^ [(-lambda) * X]
PDF, f (X) = lambda * e^ [(-lambda) * X]
Survival probability = e^ [(-lambda) * X]

20. Exponential Application
 Exponential distribution gives us average waiting
time for alpha = 1
 Suppose lambda i.e. arrival rate = 0.05
 We apply exponential distribution as follows:
 Find out PDF : =expon.dist(x,lambda,false) ;
x = waiting time, lambda = arrival rate
 Find CDF:=expon.dist(x,lambda,true) . Here
we cannot simply add PDF’s because this is a
continuous distribution

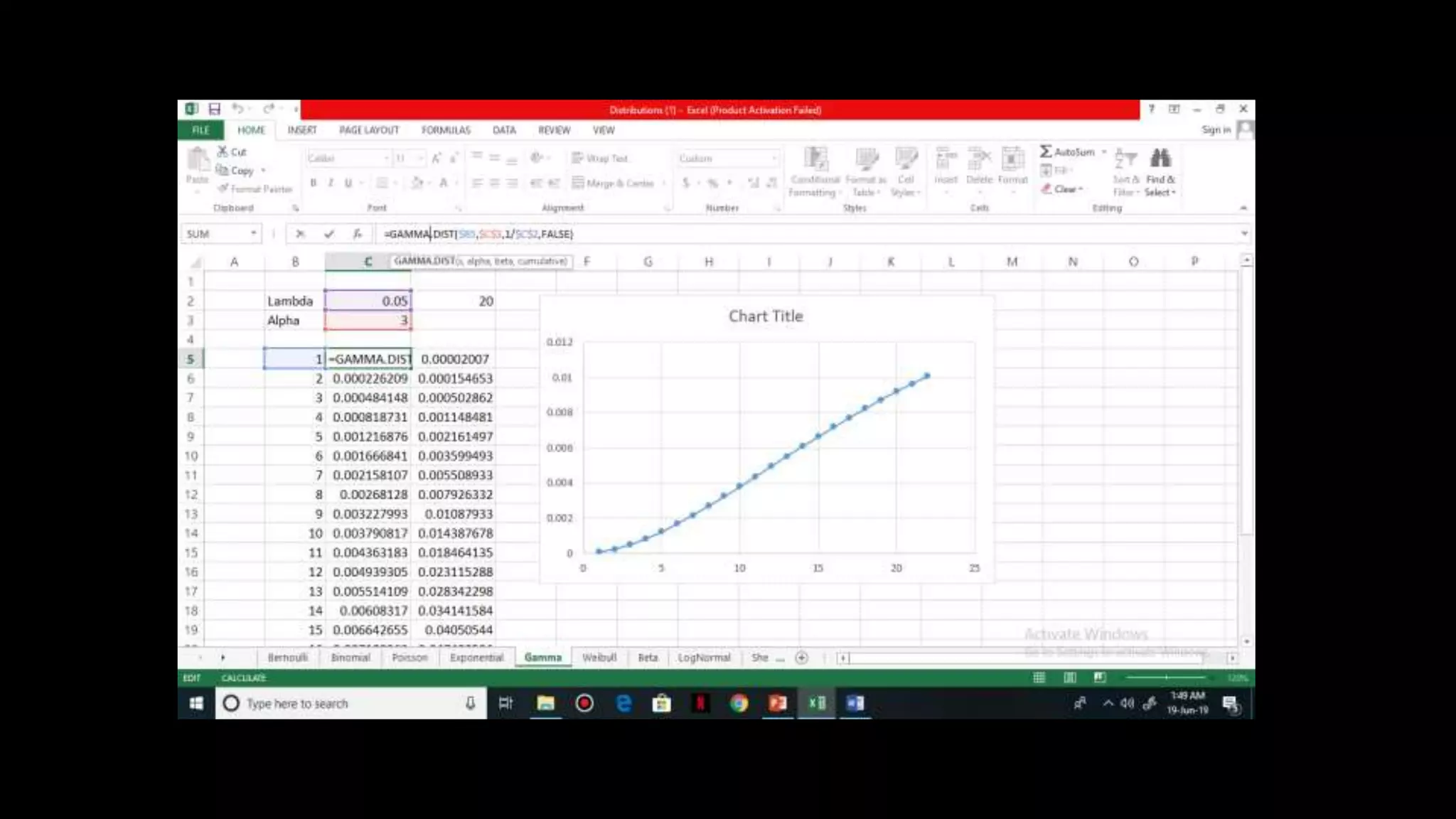
22. Gamma Distribution
It is a continuous distribution and is used to model
average waiting time for alpha = >1
Parameter of Gamma distribution = alpha & lambda
Mean = alpha / lambda
Variance = alpha / lambda^2
CDF , F(X) = 1 – e^ [(-lambda) * X]
PDF, f (X) = lambda * e^ [(-lambda) * X]
Practically used in Credit Default Swaps to model the
time it will take for triggering event to occur

23. Gamma Application – CDS
 Exponential distribution gives us average waiting
time for alpha = >1
 Suppose triggering event is 3rd default that occurs
 We need to model the probabilities of time it will
take for the 3rd default to occur
 Alpha = 3 , Default intensity i.e. lambda = 0.05,
beta = 1 / alpha
 PDF: =gamma.dist(x,alpha,beta,false)
 CDF: =gamma.dist(x,alpha,beta,true)

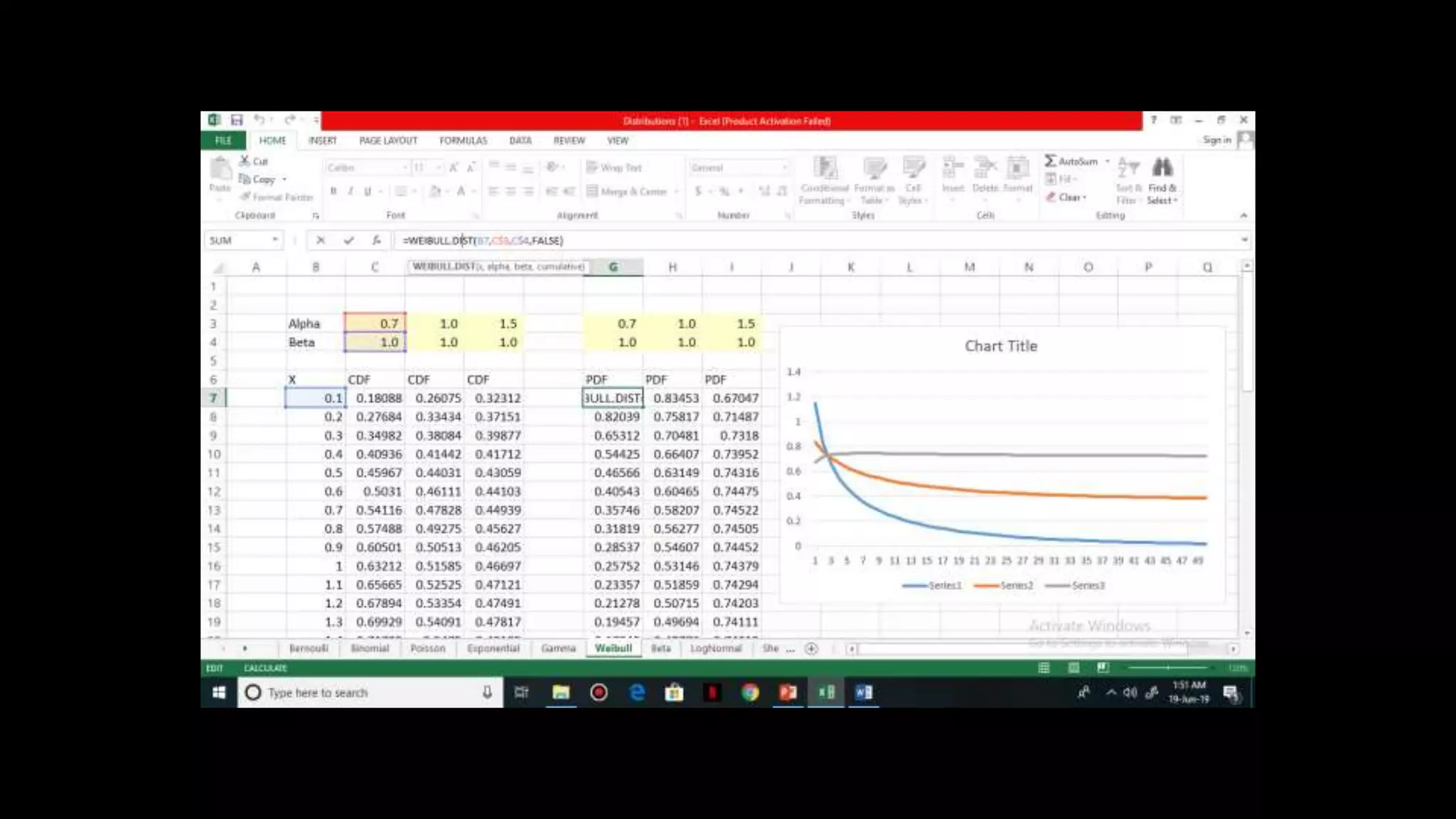
25. Weibull Distribution
Used to model the time it will take for the machine to
fail given the failure rate of lambda
Change in failure rate (Constant/Increase/Decrease)
is captured by Alpha
If failure rate is constant, alpha = 0  exponential
If failure rate increases, alpha>1  Ageing problem
If failure rate decreases, alpha<1  Teething problem
CDF, F(X) = 1 – e^{[(-lambda) * x]^alpha}
Beta = 1 / alpha

26. Weibull Application
 Suppose, X i.e. time = 0.5 years, Beta (failure rate)
= 1, Alpha = 0.7 and probability of that period =
0.45
 We can interpret that, the probability of machine
failing in next 0.5 years is with a failure rate of 1
and failure decreasing with age ( alpha < 1) is
0.45 or 45%
 Function to be used:
PDF: =Weibull.dist(x,alpha,beta,false)
CDF: =Weibull.dist(x,alpha,beta,true)
 Weibull distribution is used for 3 different alpha’s
here. Please refer the excel sheet snapshot

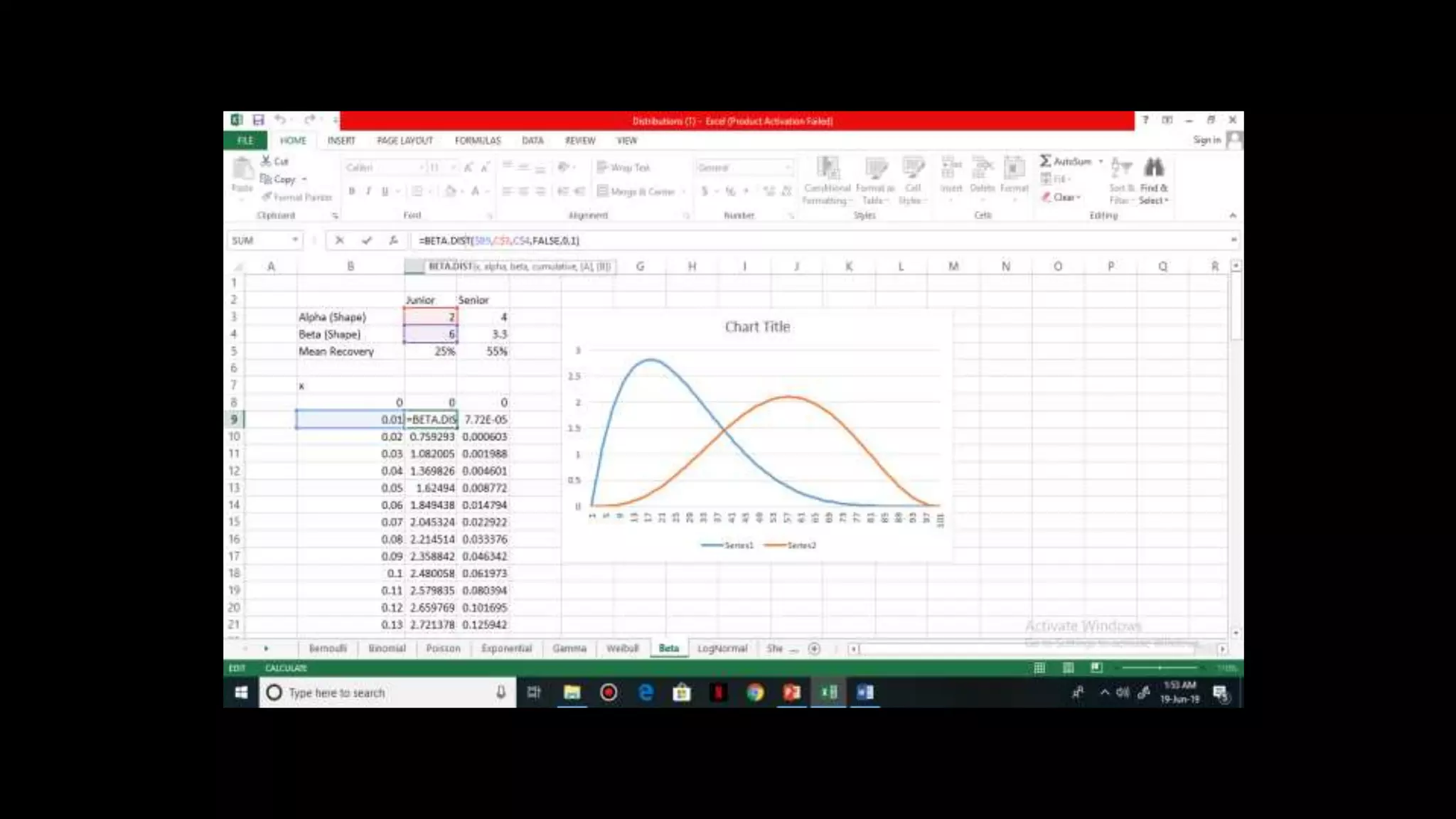
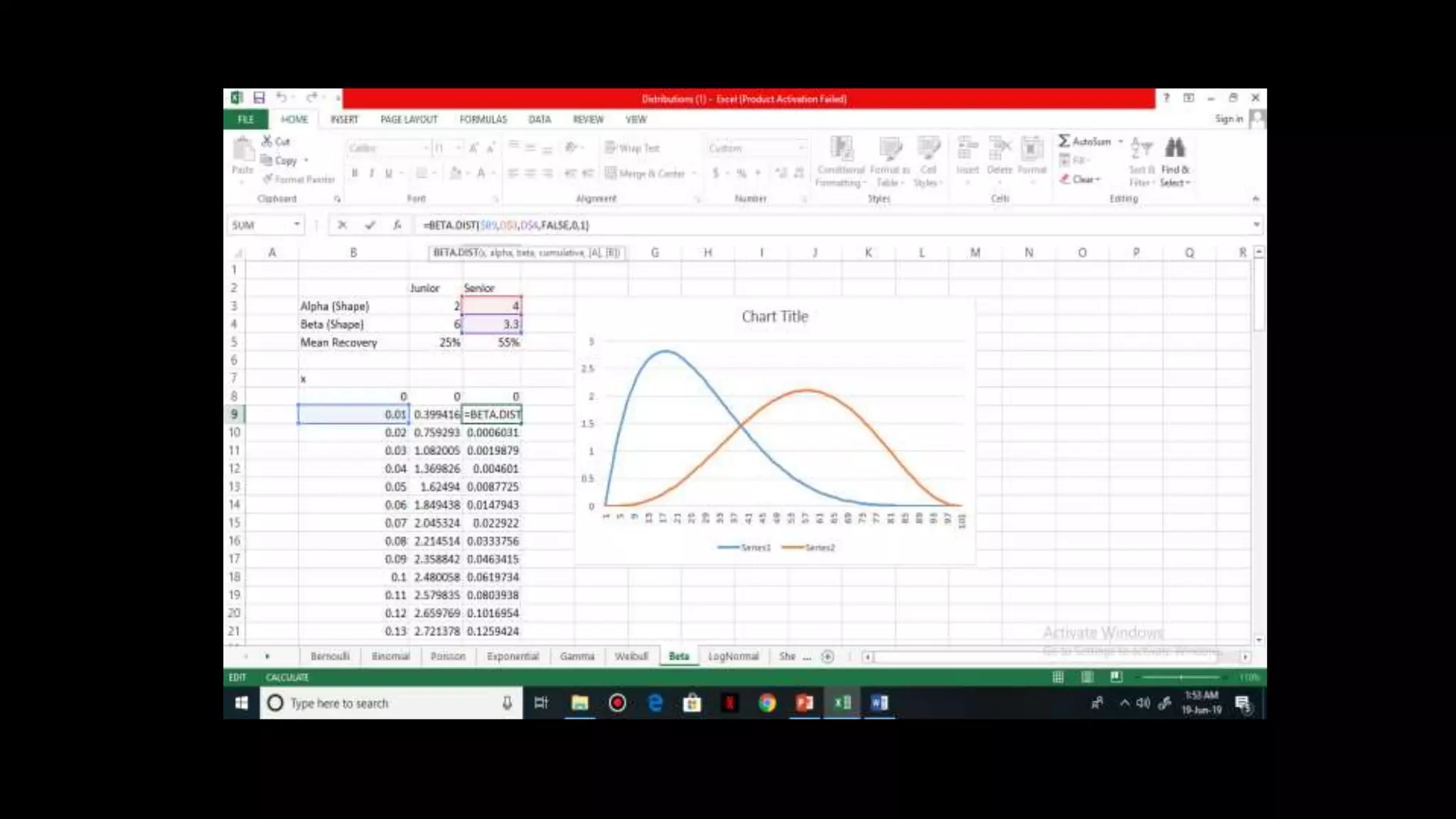
28. Beta Distribution
It is a continuous distribution and is used to model
recovery rate
Parameters of beta distribution = alpha & beta
Mean = alpha / alpha + beta
CDF, F(X) = 1 – e^{[(-lambda) * x]^alpha}
Beta = 1 / alpha

31. Log-normal Distribution
Generally used to model the stock prices (since
stock prices range from zero to infinity)
If something follows normal distribution, Ln of
something follows log-normal distribution
Parameters = Mean and Sigma from normal
distribution
Mean = e^mu + ½ * sigma^2
Product of two or more log-normally distributed
random number is log-normal

32. Log-normal Application
 Modelling the probabilities of possible stock prices
 Current price = 100, Rate of return on the stock =
8%, Volatility = 30%, Time = 3 years
 CDF: =NormSdist((LN(ST)-LN(S0) – (return – ½
* sigma^2 ) * T / Sigma * Sqrt.(T)))
 For example, the probability of stock price going
up to 140/- is 67.2% and exactly being 140 is
0.50% (Refer the excel snapshot)

35. Thank you