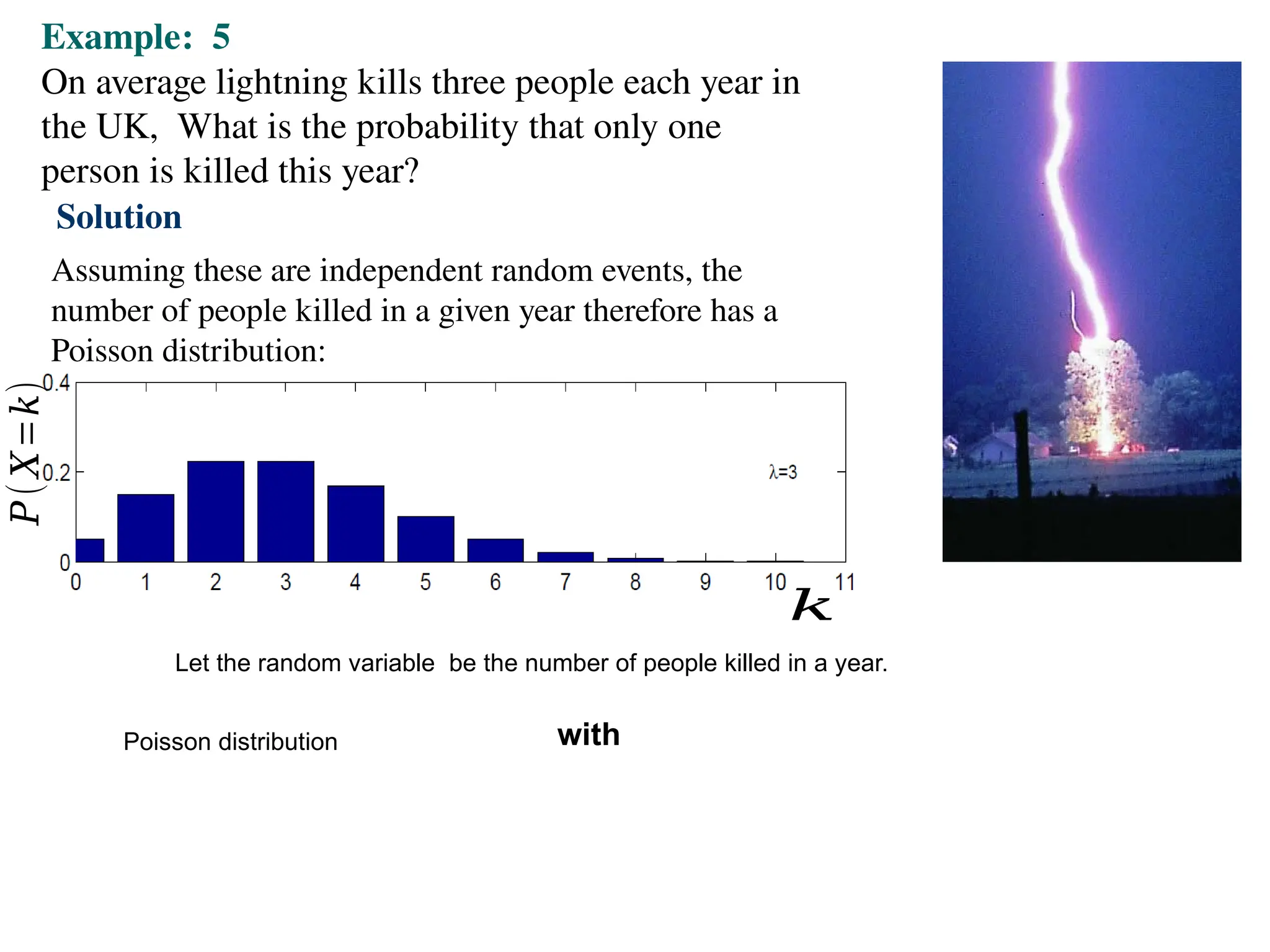
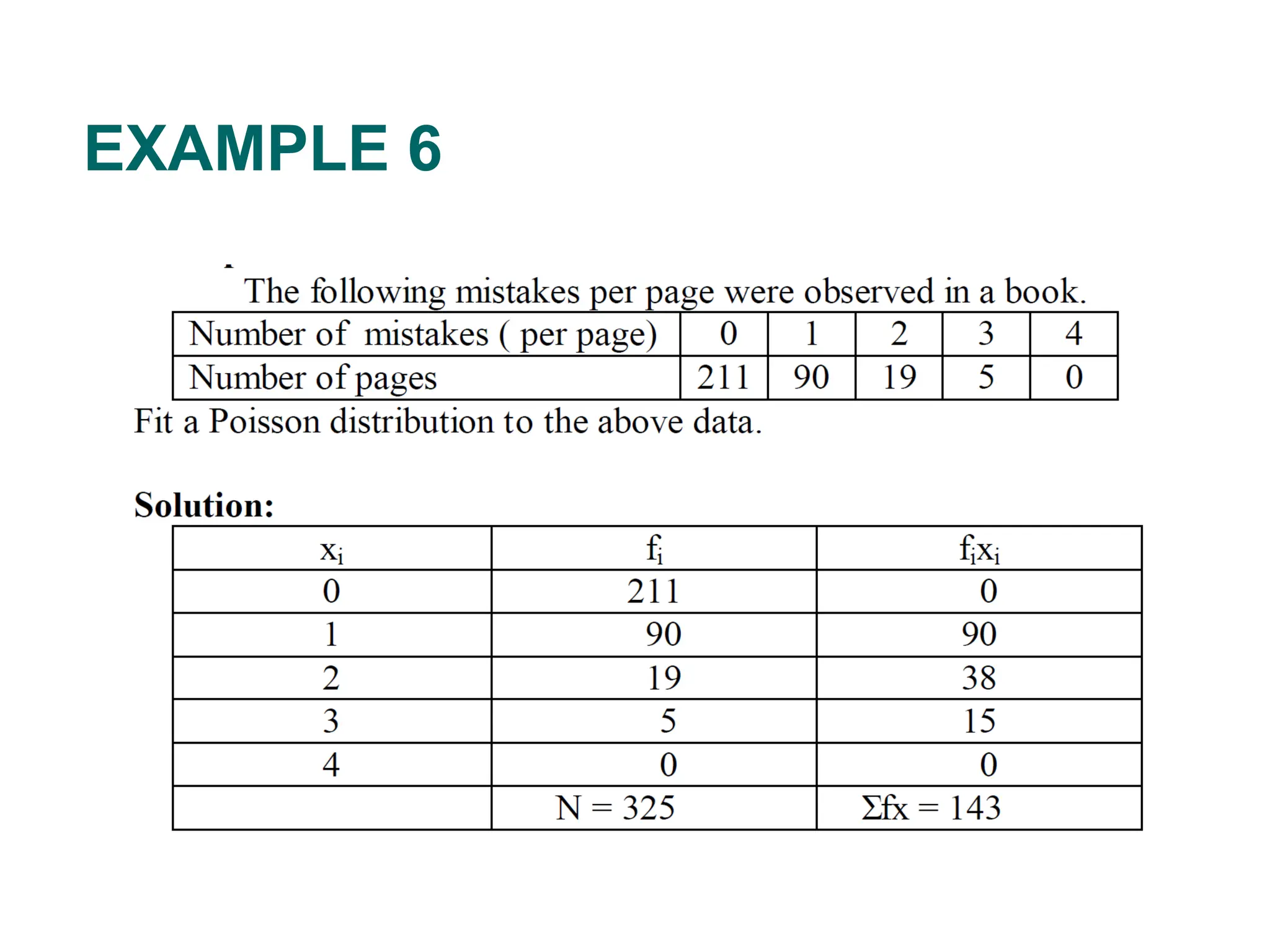
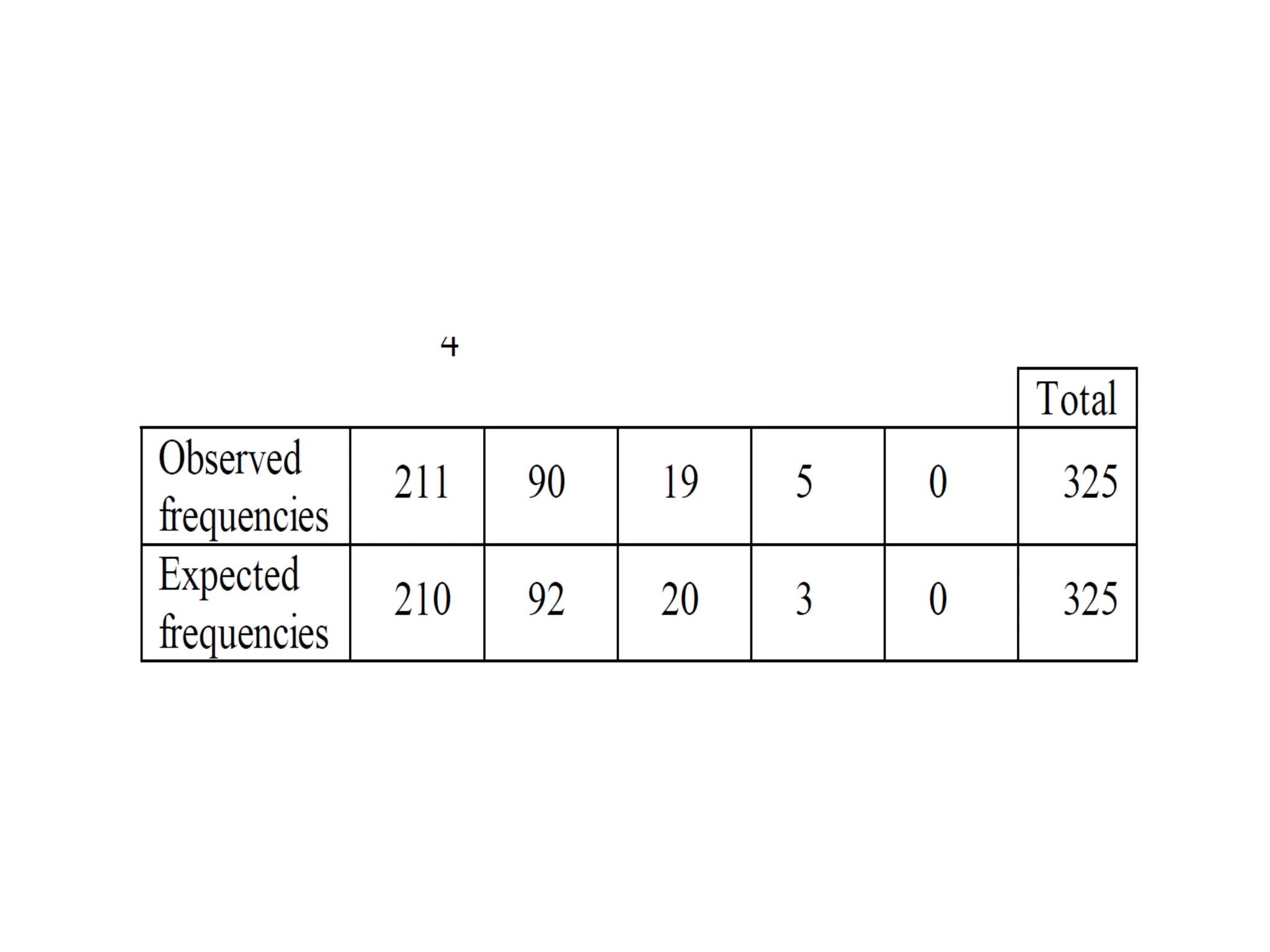
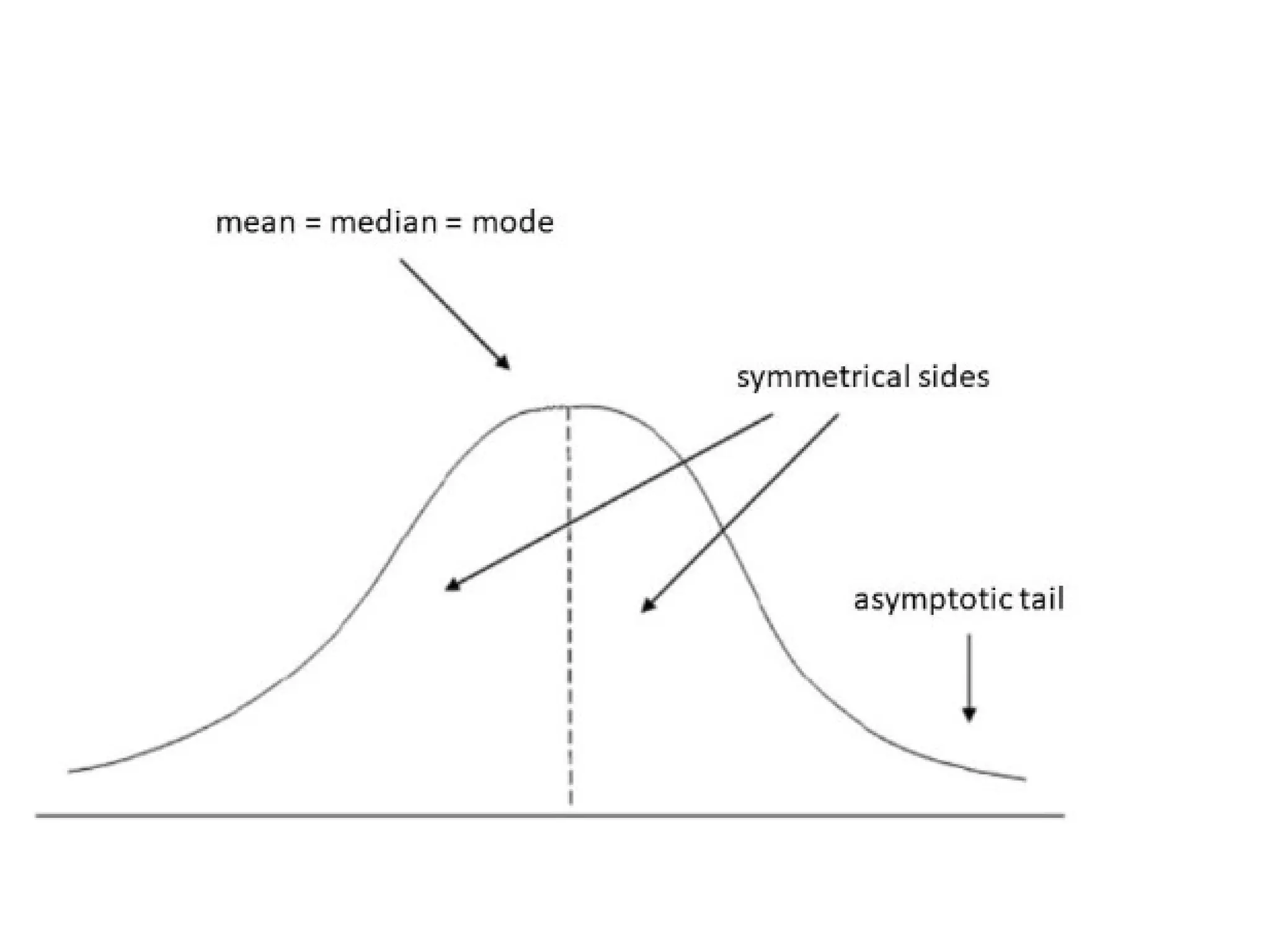
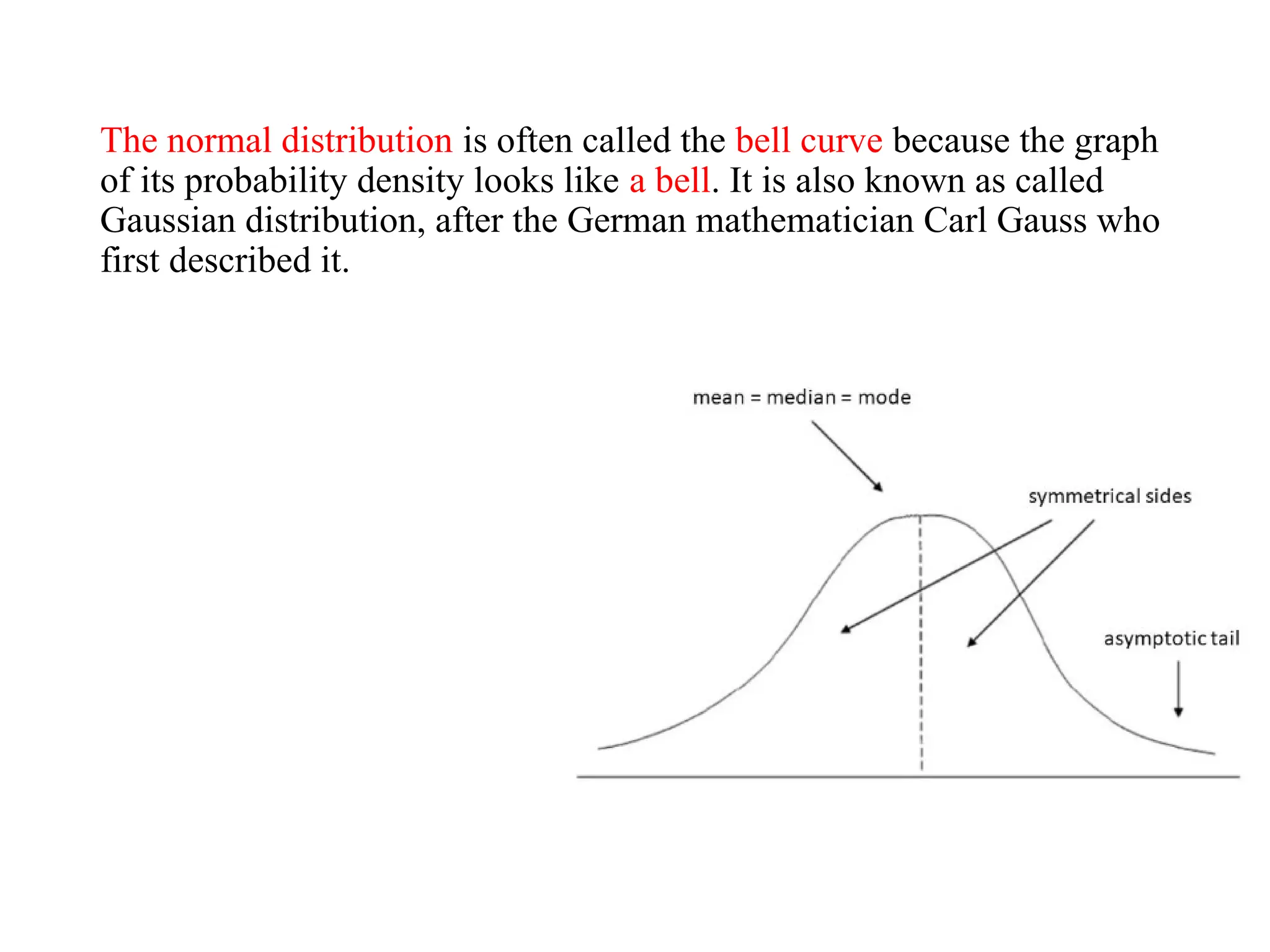
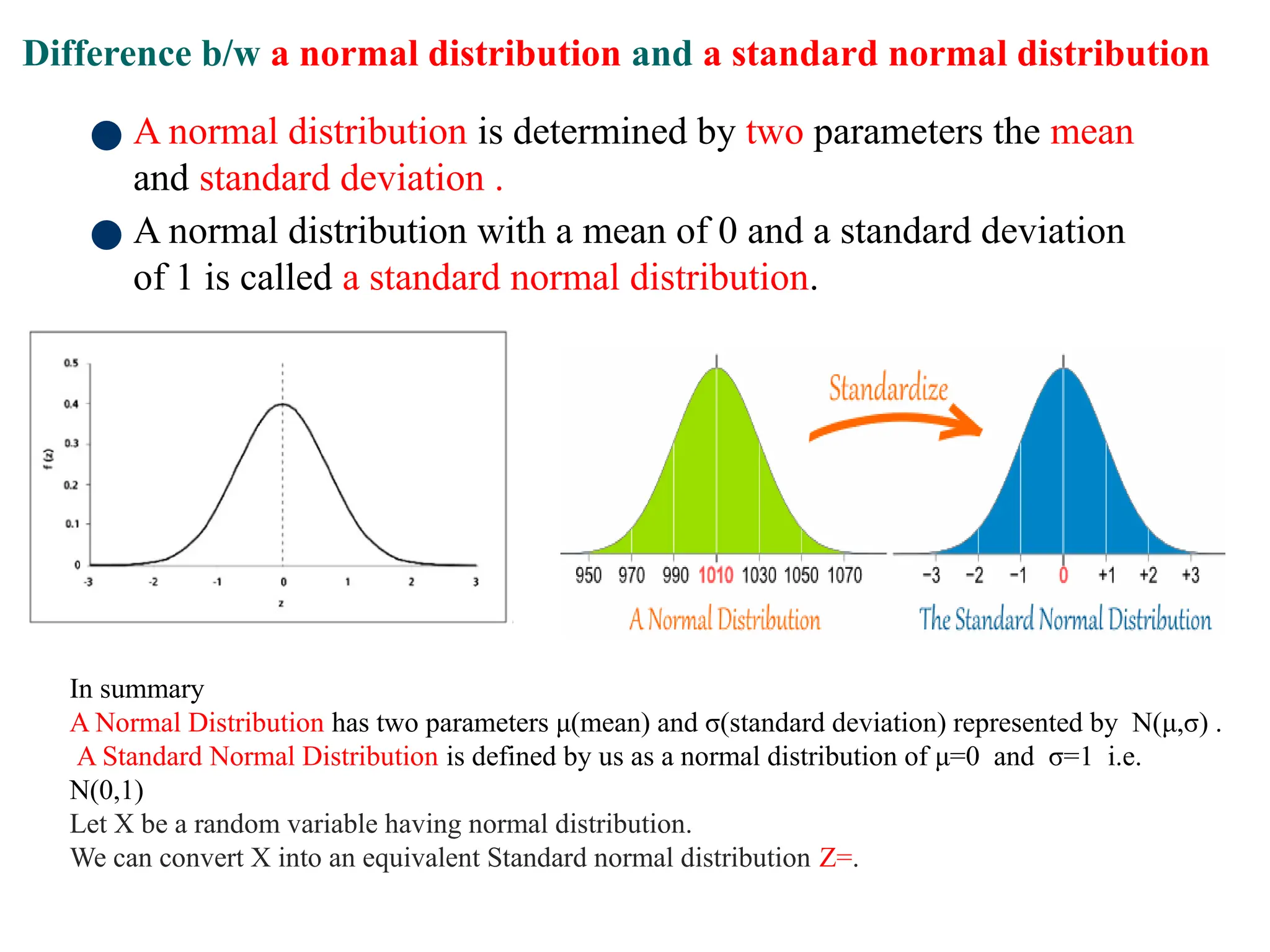
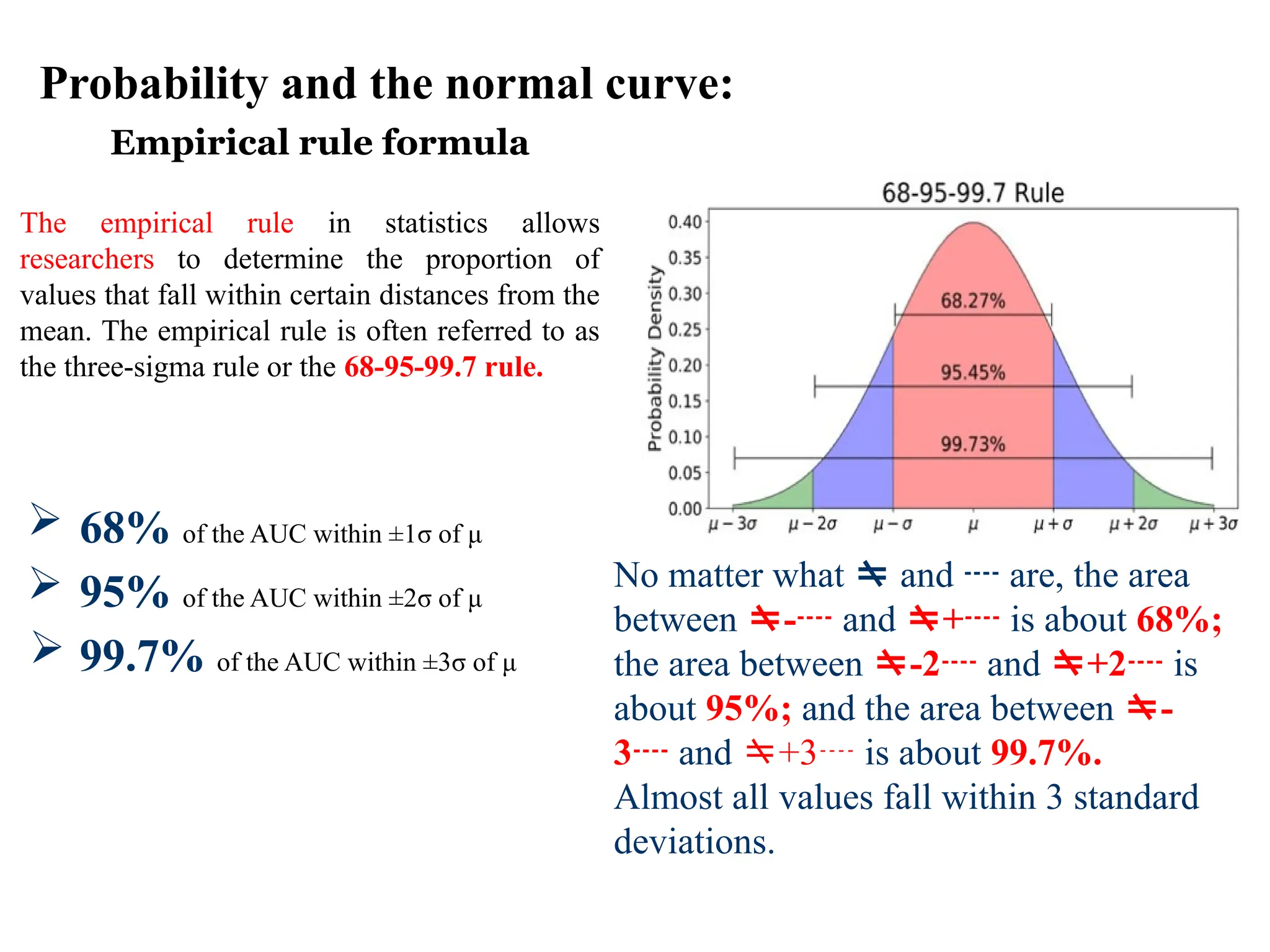
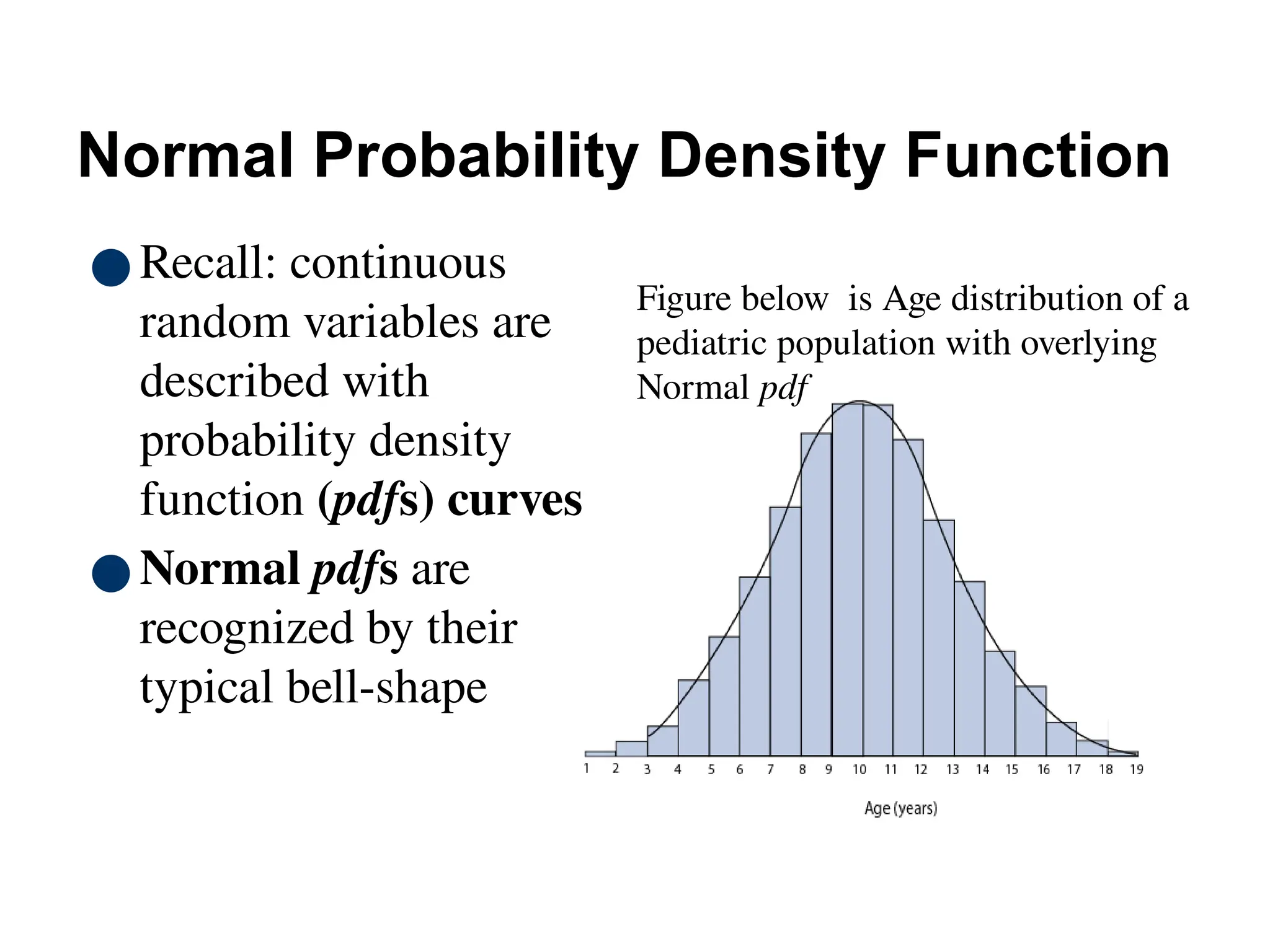
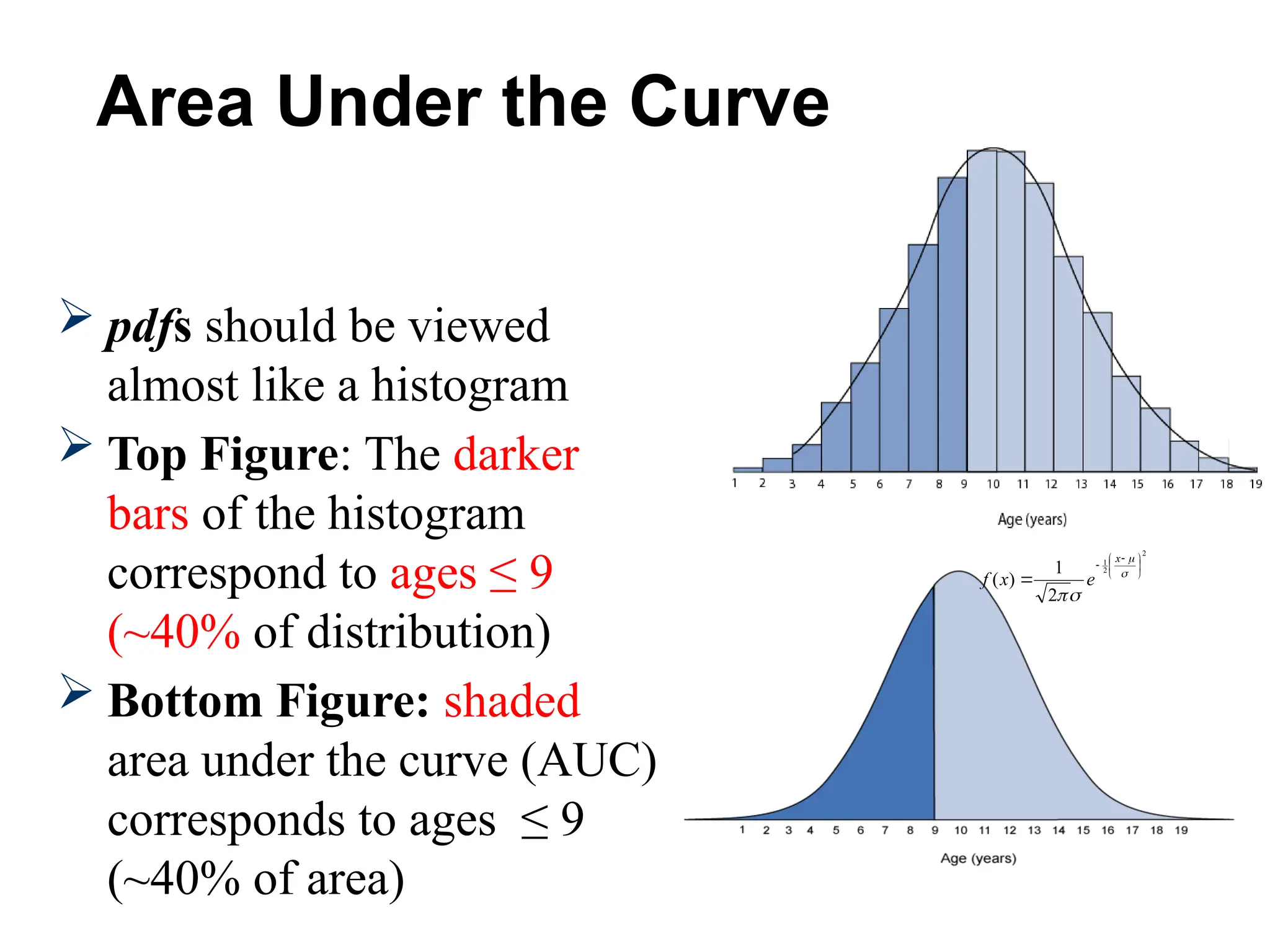
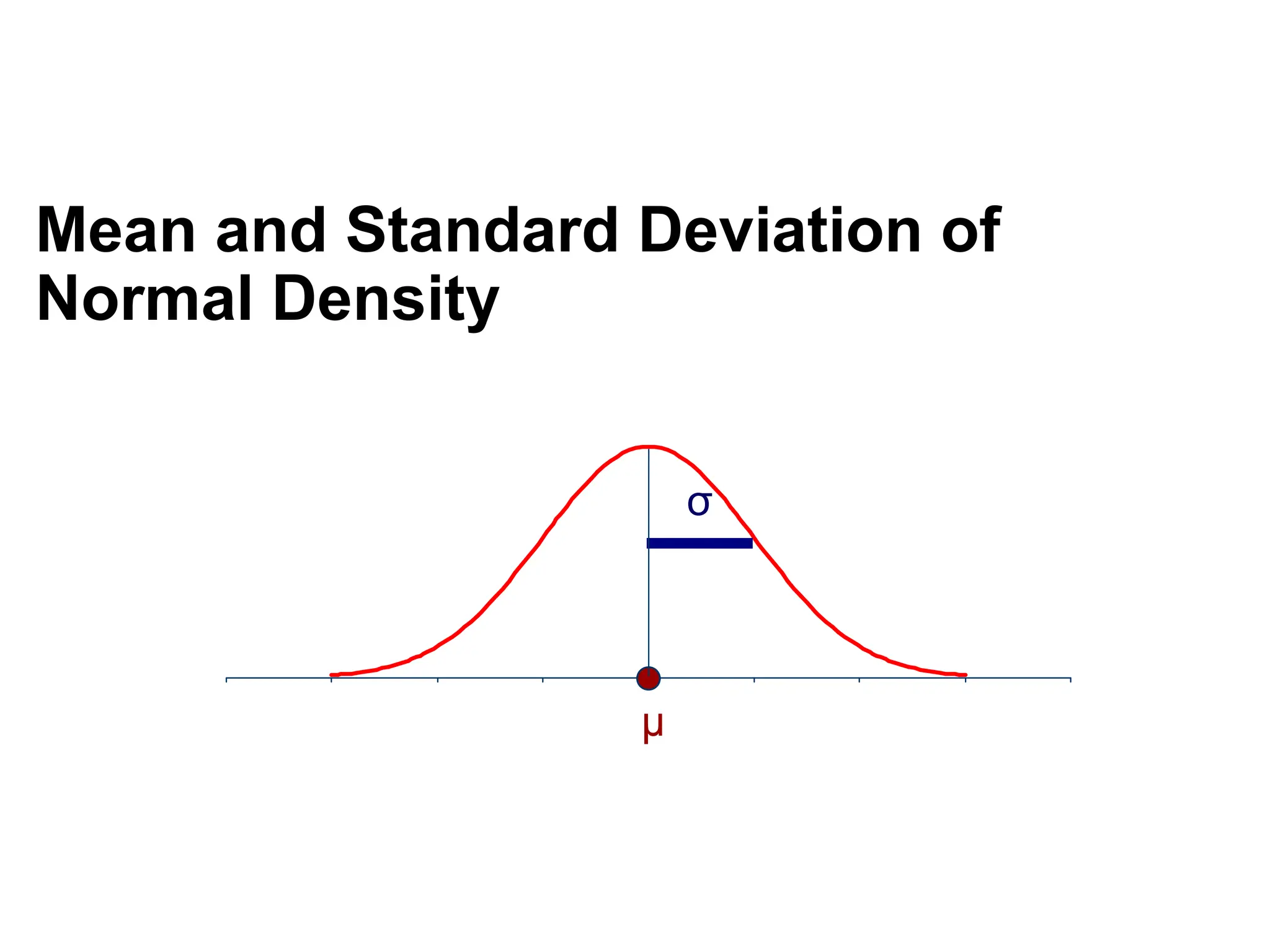
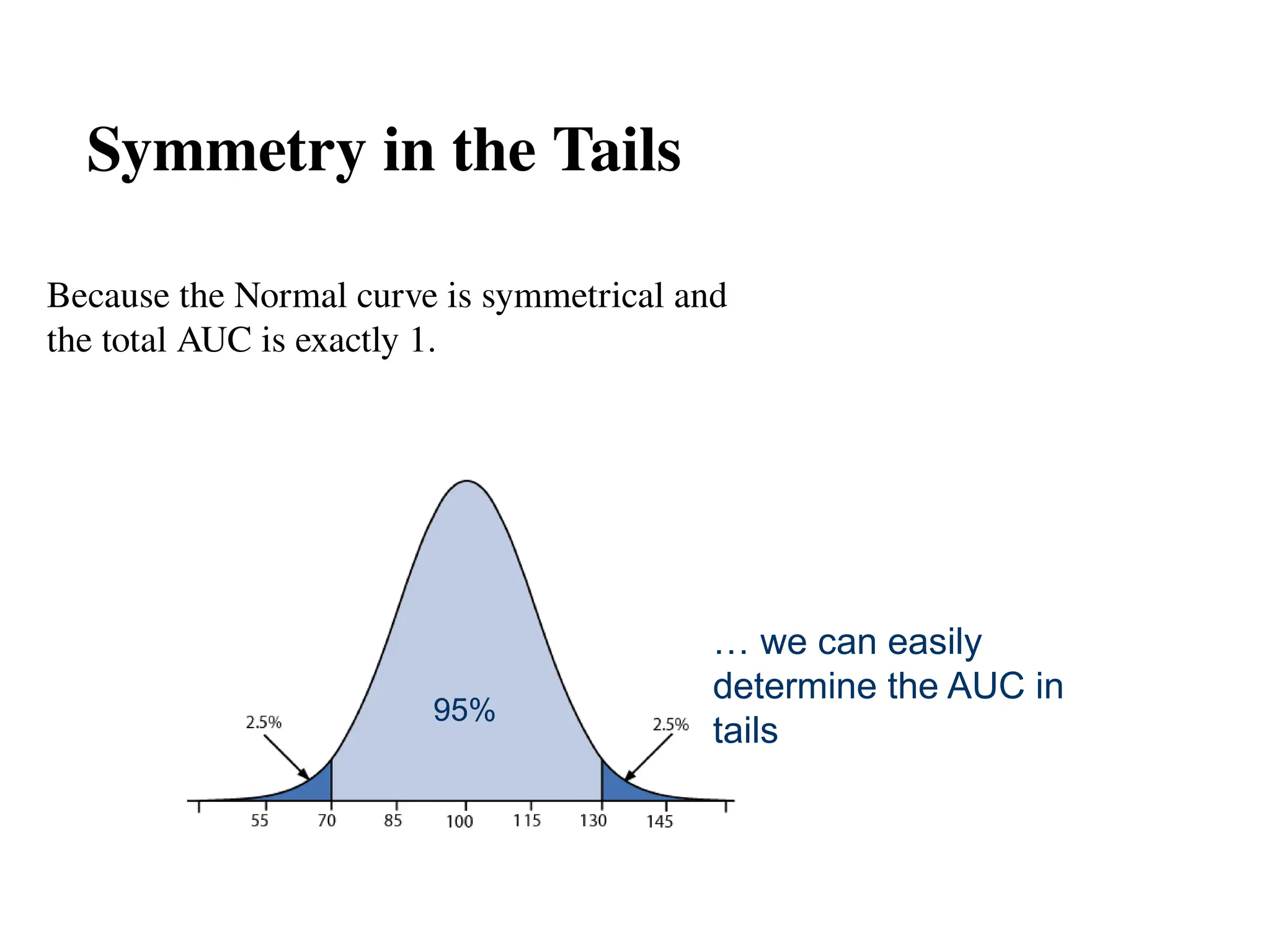
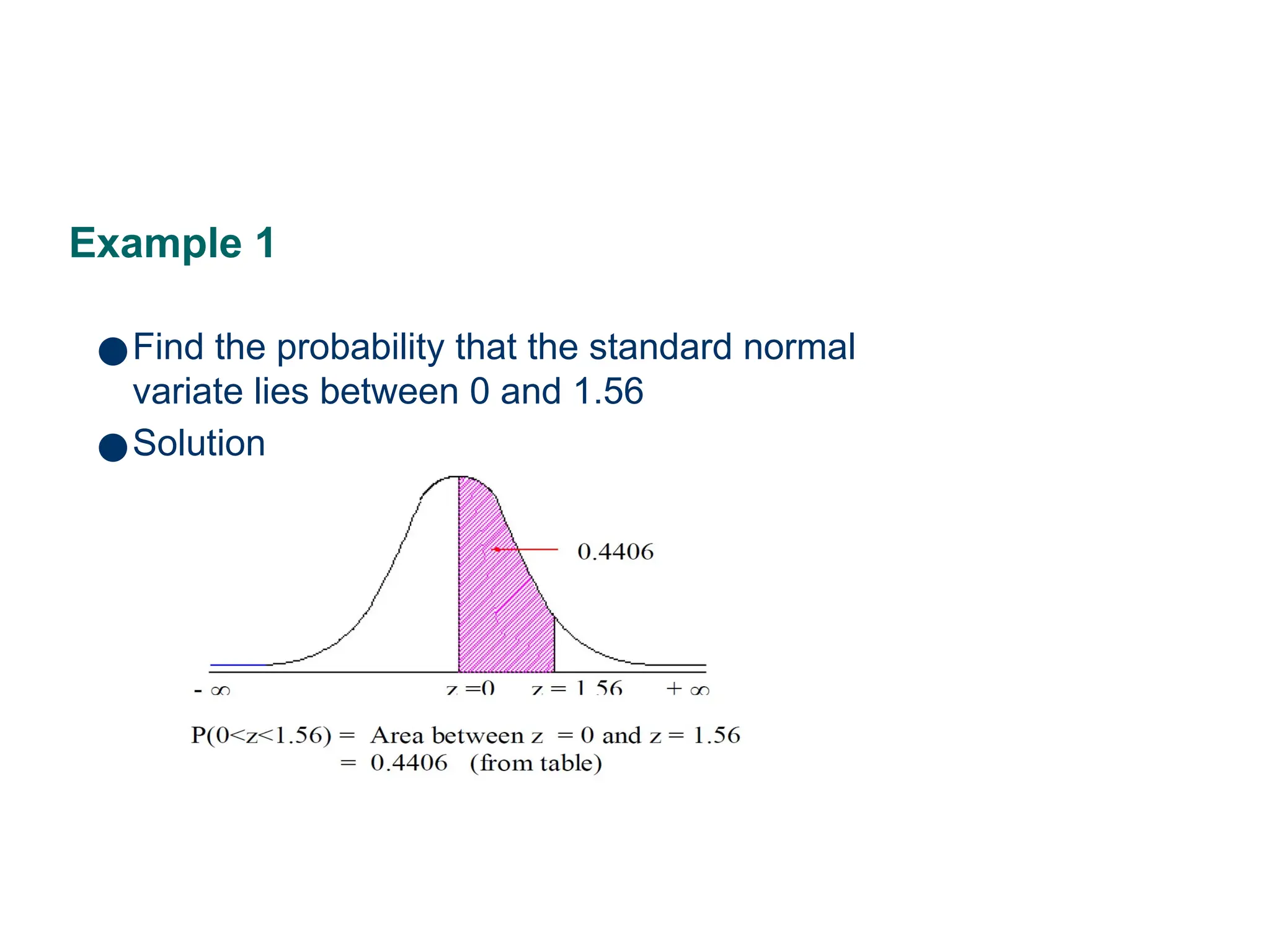
The document discusses several important theoretical distributions in probability and statistics, including the binomial, Poisson, and normal distributions. It covers definitions, properties, applications, and various examples for each distribution, illustrating their practical use in fields such as military, telecommunications, and other industries. Key concepts like Bernoulli trials, mean, variance, and the empirical rule for normal distribution are also highlighted.

1. Probability and Random process
Chapter :4
SOME IMPORTANT
THEORETICAL DISTRIBUTIONS
Eng. Abdirahman Farah
c.raxmaanfc@gmail.com

2. GOALS
2
 Binomial Distribution
 Properties of Binomial Distributions
 Summary and Applications
 Poisson Distributions
 The Normal Distribution
 Relationships between Binomial and
Normal Distributions
 Relationships between Binomial and
Poisson Distributions

3. 3

4. 4
Two events are said to be complementary when one event occurs
if and only if the other does not. The probabilities of two
complimentary events add up to 1.

5. 5

6. 6
Where P and q should not be greater than 1

7. 7
●Suppose that we have an experiment such
as tossing a coin or die repeatedly or
choosing a marble from an urn repeatedly.
Each toss or selection is called a trial. In any
single trial there will be a probability
associated with a particular event such as
head on the coin, four on the die, or selection
of a specific color marble. In some cases this
probability will not change from one trial to
the next (as in tossing a coin or die).

8. 8
●Such trials are then said to be independent
and are often called Bernoulli trials after
James Bernoulli who investigated them at the
end of the seventeenth century.
●Let p be the probability that an event will
happen in any single Bernoulli trial (called
the probability of success). Then q = 1 − p is
the probability that the event will fail to
happen in any single trial (called the
probability of failure).

9. Examples of Bernoulli’ s Trails are:
●Examples of Bernoulli’ s Trails are:
●1) Toss of a coin (head or tail)
●2) Throw of a die (even or odd number)
●3) Performance of a student in an
examination (pass or fail)
9

10. Binomial Distribution:
10
●The probability that the event will happen
exactly x times in n trials (i.e., x successes
and n – x failures will occur) is given by the
probability function

11. Condition for Binomial Distribution:
●We get the Binomial distribution under the
following experimental conditions.
●1) The number of trials ‘ n’ is finite.
●2) The trials are independent of each other.
●3) The probability of success ‘ p’ is constant
for each trial.
●4) Each trial must result in a success or a
failure.
11

12. Example 1.
12
A quiz consists of 10 multiple-choice questions. Each question
has 5 possible answers, only one of which is correct.
Ali plans to guess the answer to each question.
Find the probability that Ali gets
a. one answer correct.
b. all 10 answers correct.

13. Example 2.
The Probability that a bomb dropped from a plane will strike
the target is 1/5, if six bombs are dropped find the probability that
exactly two will strike the target.
Solution
● Given, n=6, P(bomb will strike the target) , p=0.2
● P(bomb will not strike the target) , q = 1-p=1-0.2=0.8
13

14. Activity.
14
●Find the probability of getting exactly 2 heads in
6 tosses of a fair coin
●solution
= 0.234375

15. Example 3.
15
●Eight coins are tossed simultaneously. Find
the probability of getting at least six heads.

16. Solution
16

17. 17
17

18. 18
Activity 2.
●Ten coins are tossed simultaneously.
Find the probability of getting
● (i) at least seven heads
●(ii) exactly seven heads
●(iii) at most seven heads

19. Solution
19

20. 20

21. 21

22. Exercise
●20 wrist watches in a box of 100 are
defective. If 10 watches are selected at
random, find the probability that
●(i) 10 are defective
●(ii) 10 are good
●(iii) at least one watch is defective
●(iv) at most 3 are defective.
22

23. solution
23

24. i) Probability of selecting 10 defective watches
24

25. II AND III
25

26. iv) Probability of selecting at most 3 defective
watches
26

27. Properties of Binomial Distributions
27

28. EXAMPLE 4
●Toss a fair coin 100 times, and
count the number of heads that
appear. Find the
i. mean,
ii.variance,
iii.and standard deviation of this
experiment.
28

29. Solution
●
29

30. Fitting of Binomial Distribution
Remember!
The random variable itself is the process dictating how the observation
comes about.
 Binomial distribution summarizes the number of trials, or observations
when each trial has the same probability of attaining one particular
value.
 The binomial distribution determines the probability of observing a
specified number of successful outcomes in a specified number of trials.
 In probability and statistics, a realization, observation, or observed
value, of a random variable is the value that is actually observed (what
actually happened).
 Fitting of probability distribution to a series of observed data helps to
predict the probability or to forecast the frequency of occurrence of the
required variable in a certain desired interval.
 There are many probability distributions of which some can be fitted
more closely to the observed frequency of the data than others,
depending on the characteristics of the variables. Therefore one needs to
select a distribution that suits the data well.
30

31. Fitting of Binomial Distribution
31

32. Example 5
32
Fit a binomial distribution and estimate the expected frequencies

33. Solution
33

34. 34

35. 35

36. Summary and Applications of Binomial Distribution
36

37. 37
Its also used Military in Applications ( hit, mission)

38. End Binomial Distribution
38

39. POISSON DISTRIBUTION
 A Poisson distribution, named after French
mathematician and physicist Siméon Denis Poisson in
1837.
It can be used to estimate how many times an event is
likely to occur within "X" periods of time.
Poisson distributions are used when the variable of
interest is a discrete count variable.
39

40. Distributions
● Poisson distribution is probably one of the most practical statistical
distributions in answering lots of questions in today world.
● The use cases can cover various problems from business, banking,
insurance, science, medical and risk management.
● A Poisson distribution can be used to estimate how likely it is that
something will happen "X" number of times.
For example
● if the average number of people who buy cheeseburgers from a fast-
food chain on a Friday night at a single restaurant location is 200, a
Poisson distribution can answer questions such as, "What is the
probability that more than 300 people will buy burgers?“
40

41. Poisson distribution
If events happen independently of each other, with average number of
events in some fixed interval , then the distribution of the number of
events in that interval is Poisson.
A random variable has the Poisson distribution with parameter (> 0) if

42. Characteristics of Poisson
Distribution:
42

43. 43

44. Poisson Distribution Summary
Describes discrete random variable that is the number of independent and randomly occurring
events, with mean number . Probability of such events is
𝑃 (𝑋 =𝑘)=
𝑒− 𝜆
𝜆𝑘
𝑘!
Mean and variance:
if then where
Approximation to Binomial for large and small :
The sum of Poisson variables is also Poisson, with average number

45. Example 1.
45
Suppose that trucks arrive at a receiving
dock with an average arrival rate of 3
per hour. What is the probability
exactly 5 trucks will arrive in a two-
hour period?
Reminder:
In two hours mean number is .
𝑃 (𝑋 =𝑘=5)=
𝑒− 𝜆
𝜆𝑘
𝑘!
=
𝑒− 6
65
5!
=0.16

46. Example 2.
Telecommunication
Messages arrive at a switching centre at random and at an average rate of
1.2 per second.
(a) Find the probability of 5 messages arriving in a 2-sec interval.
(b) For how long can the operation of the centre be interrupted, if the
probability of losing one or more messages is to be no more than 0.05?
Solution:
Times of arrivals form a Poisson process, rate sec.
(a) Let Y = number of messages arriving in a 2-sec interval.
Then Y ~ Poisson, mean number
𝑃 (𝑌 =𝑘=5)=
𝑒− 𝜆
𝜆𝑘
𝑘!
=
𝑒− 2.4
2.45
5!
=0.060

47. Question: (b) For how long can the operation of the centre be interrupted, if
the probability of losing one or more messages is to be no more than 0.05?
(b) Let the required time = t seconds. Average rate of arrival is 1.2/second.
Solution:
Let = number of messages in t seconds, so that
Poisson, with
Want P(At least one message) =
⇒ 1−𝑒− 1.2𝑡
≤ 0.05
⇒ 𝑒−1 .2𝑡
≥ 0.95
⇒−1.2𝑡 ≥ ln(0.95)=−0.05129
⇒𝑡≤0.043 seconds
⇒ 1−𝑒− 1.2𝑡
≤ 0.05
⇒ −𝑒−1.2𝑡
≤ 0.05− 1
𝑃 (𝑘=0)=
𝑒− 𝜆
𝜆𝑘
𝑘!
=
𝑒
− 1.2𝑡
(1.2𝑡 )0
0!
=𝑒
−1.2𝑡

48. ● Example 3: Calls per Hour at a Call Center
● Call centers use the Poisson distribution to model the number of expected
calls per hour that they’ll receive so they know how many call center reps
to keep on staff.
● suppose a given call center receives 10 calls per hour. find the probability
that a call center receives 0, 1, 2, 3 …calls in a given hour:
● Solution
• P(X = 0 calls) = 0.00005
• P(X = 1 call) = 0.00045
• P(X = 2 calls) = 0.00227
• P(X = 3 calls) = 0.00757
● And so on.
● This gives call center managers an idea of how many calls they’re likely to
receive per hour and enables them to manage employee schedules based
on the number of expected calls.

49. Activity: Number of Network Failures per Week
● Technology companies use the Poisson distribution to model the
number of expected network failures per week.
● For example, suppose a given company experiences an average of 1
network failure per week.
● find the probability that the company experiences a certain number of
network failures in a given week:
Solution
49
• P(X = 0 failures) = 0.36788
• P(X = 1 failure) = 0.36788
• P(X = 2 failures) = 0.18394

50. Example 4
50
●If the probability that an individual will suffer a bad
reaction from injection of a given serum is 0.001,
determine the probability that out of 2000
individuals, (a) exactly 3, (b) more than 2,
individuals will suffer a bad reaction.
Solution
●Mean = np = (2000)(0.001) = 2

51. Activity 1
51
51
Solution

52. Activity 2
52

53. 53

54. Example: 5
On average lightning kills three people each year in
the UK, What is the probability that only one
person is killed this year?
Assuming these are independent random events, the
number of people killed in a given year therefore has a
Poisson distribution:
Solution
with
Let the random variable be the number of people killed in a year.
Poisson distribution
𝑘
𝑃
(
𝑋=𝑘)

55. Fitting of Poisson Distribution:
55

56. EXAMPLE 6
56

57. 57
0..

58. 58

59. 59

60. Applications
60
7. Number of messages arriving at a telecommunications system in a
day
8. Number of flaws in a metre of fibre optic cable
9. Number of radio-active particles detected in a given time
4) Number of photons arriving at a CCD pixel in some exposure time
(e.g. astronomy observations)

61. Normal Distribution

62. 62
●In the preceding sections we have discussed the discrete
distributions, the Binomial and Poisson distribution.
●In this section we deal with the most important
continuous distribution, known as normal probability
distribution or simply normal distribution.
It is important for the reason that it plays a vital role in the
theoretical and applied statistics.
Introduction : NORMAL DISTRIBUTION

63. 63
The Normal Distribution Overview
●The normal distribution was first discovered by De
Moivre (English Mathematician) in 1733 as limiting case
of binomial distribution.
● Later it was applied in natural and social science by
Laplace (French Mathematician) in 1777.
● The normal distribution is also known as Gaussian
distribution in honor of German mathematician Karl
Friedrich Gauss(1809).

64.  The normal distribution (or Gaussian) is a continuous probability
distribution that is symmetrical on both sides of the mean, so the
right side of the center is a mirror image of the left side.
 The area under the normal distribution curve represents probability
and the total area under the curve sums to one.
 Most of the continuous data values in a normal distribution tend to
cluster around the mean, and the further a value is from the mean,
the less likely it is to occur.
 The tails are asymptotic, which means that they approach but never
quite meet the horizon (i.e. x-axis). For a perfectly normal
distribution the mean, median and mode will be the same value,
visually represented by the peak of the curve.
The Normal Distribution Overview

65. 65

66. The normal distribution is often called the bell curve because the graph
of its probability density looks like a bell. It is also known as called
Gaussian distribution, after the German mathematician Carl Gauss who
first described it.

67. Difference b/w a normal distribution and a standard normal distribution
● A normal distribution is determined by two parameters the mean
and standard deviation .
● A normal distribution with a mean of 0 and a standard deviation
of 1 is called a standard normal distribution.
In summary
A Normal Distribution has two parameters μ(mean) and σ(standard deviation) represented by N(μ,σ) .
A Standard Normal Distribution is defined by us as a normal distribution of μ=0 and σ=1 i.e.
N(0,1)
Let X be a random variable having normal distribution.
We can convert X into an equivalent Standard normal distribution Z=.

68. 68
Probability and the normal curve:
 68% of the AUC within ±1σ of μ
 95% of the AUC within ±2σ of μ
 99.7% of the AUC within ±3σ of μ
Empirical rule formula
The empirical rule in statistics allows
researchers to determine the proportion of
values that fall within certain distances from the
mean. The empirical rule is often referred to as
the three-sigma rule or the 68-95-99.7 rule.
No matter what  and  are, the area
between - and + is about 68%;
the area between -2 and +2 is
about 95%; and the area between -
3 and +3 is about 99.7%.
Almost all values fall within 3 standard
deviations.

69. A continuous random variable is said to be normally distributed with mean 
and variance 2
if its probability density function is
Used to specify the probability of a random variable (e.g. X) falling within a
particular range of values.
Non negative everywhere.
It’s integral over the entire space is 1, meaning that the area below the curve
is always equal to 1.
We will denote it as f(x).
Probability density function

70. 70
Normal Probability Density Function
●Recall: continuous
random variables are
described with
probability density
function (pdfs) curves
●Normal pdfs are
recognized by their
typical bell-shape
Figure below is Age distribution of a
pediatric population with overlying
Normal pdf

71. 71
Area Under the Curve
 pdfs should be viewed
almost like a histogram
 Top Figure: The darker
bars of the histogram
correspond to ages ≤ 9
(~40% of distribution)
 Bottom Figure: shaded
area under the curve (AUC)
corresponds to ages ≤ 9
(~40% of area)
2
2
1
2
1
)
(





 

 



x
e
x
f

72. 72
Parameters μ and σ
●Normal pdfs have two parameters
μ - expected value (mean “mu”)
σ - standard deviation (sigma)
σ controls spread
μ controls location

73. 73
Mean and Standard Deviation of
Normal Density
μ
σ

74. 74
Standard Deviation σ
●Points of inflections one
σ below and above μ
●Practice sketching Normal
curves
●Feel inflection points
(where slopes change)
●Label horizontal axis with
σ landmarks

75. Normal distribution is defined by its mean
and standard dev.
E(X)= =
Var(X)=2
=
Standard Deviation(X)=
dx
e
x
x







2
)
(
2
1
2
1 



2
)
(
2
1
2
)
2
1
(
2













dx
e
x
x

76. 68-95-99.7 Rule in Math terms…
997
.
2
1
95
.
2
1
68
.
2
1
3
3
)
(
2
1
2
2
)
(
2
1
)
(
2
1
2
2
2













































dx
e
dx
e
dx
e
x
x
x

77. 77
Example: 68-95-99.7 Rule
Wechsler adult intelligence
scores: Normally
distributed with μ = 100
and σ = 15; X ~ N(100, 15)
● 68% of scores within
μ ± σ
= 100 ± 15
= 85 to 115
● 95% of scores within
μ ± 2σ
= 100 ± (2)(15)
= 70 to 130
● 99.7% of scores in
μ ± 3σ =
100 ± (3)(15)
= 55 to 145

78. 78
Symmetry in the Tails
… we can easily
determine the AUC in
tails
95%
Because the Normal curve is symmetrical and
the total AUC is exactly 1.

79. Properties of normal distribution:
79

80. 80
Area properties of Normal curve:

81. standard variable
81

83. Example 1
83
●Find the probability that the standard normal
variate lies between 0 and 1.56
●Solution

84. Example 2
84

85. 85

86. Example 3
• For example: What’s the probability of getting a math SAT(Scholastic Aptitude Test”)
score of 575 or less, =500 and =50?
5
.
1
50
500
575



Z
 i.e., A score of 575 is 1.5 standard deviations above the mean

 











5
.
1
2
1
575
200
)
50
500
(
2
1 2
2
2
1
2
)
50
(
1
)
575
( dz
e
dx
e
X
P
Z
x


But to look up Z= 1.5 in standard normal chart
P(X)= 0.9332

87. Standard Normal Distribution Table

88. End of Chapter 4
88
88

89. 89

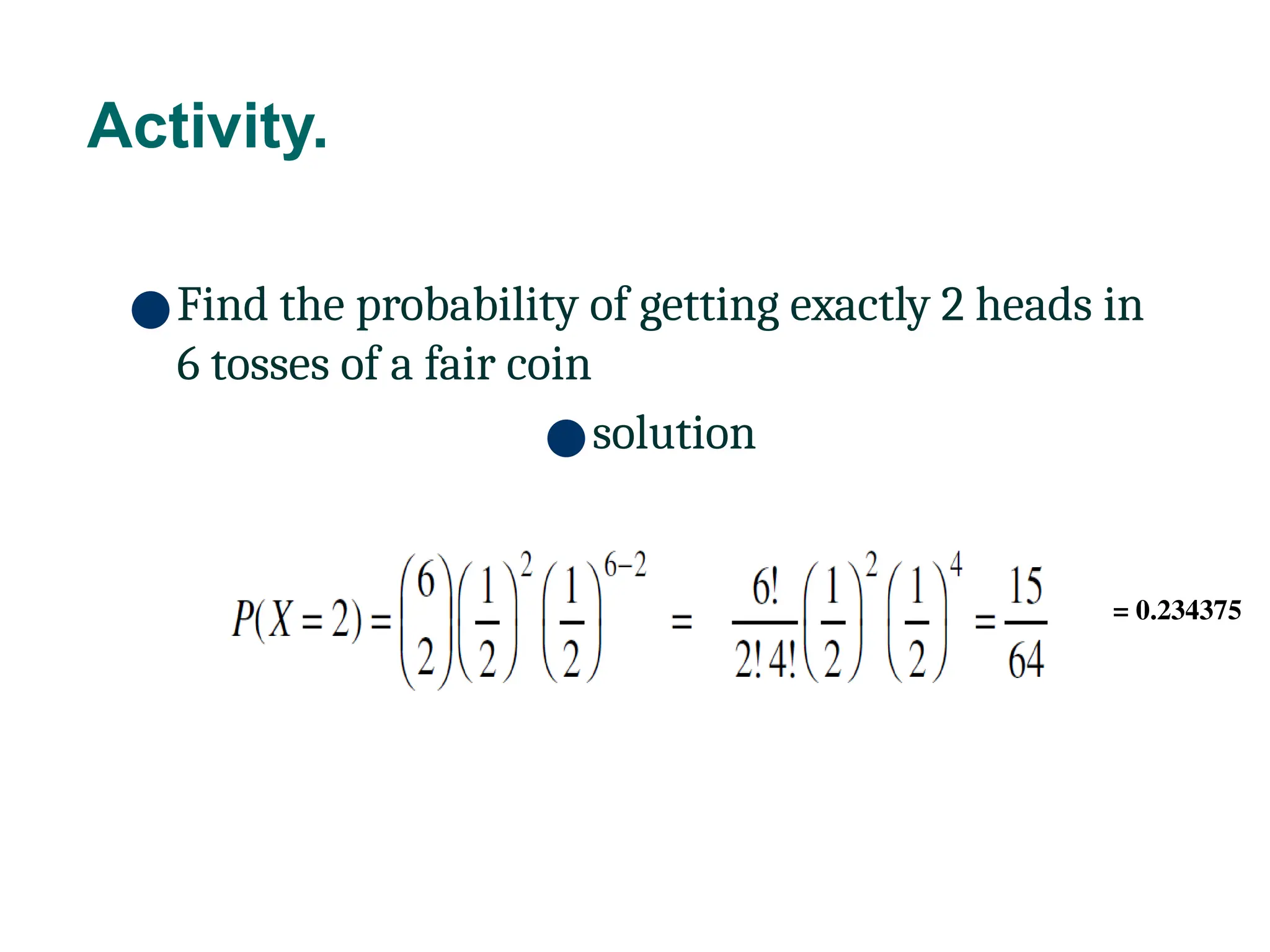
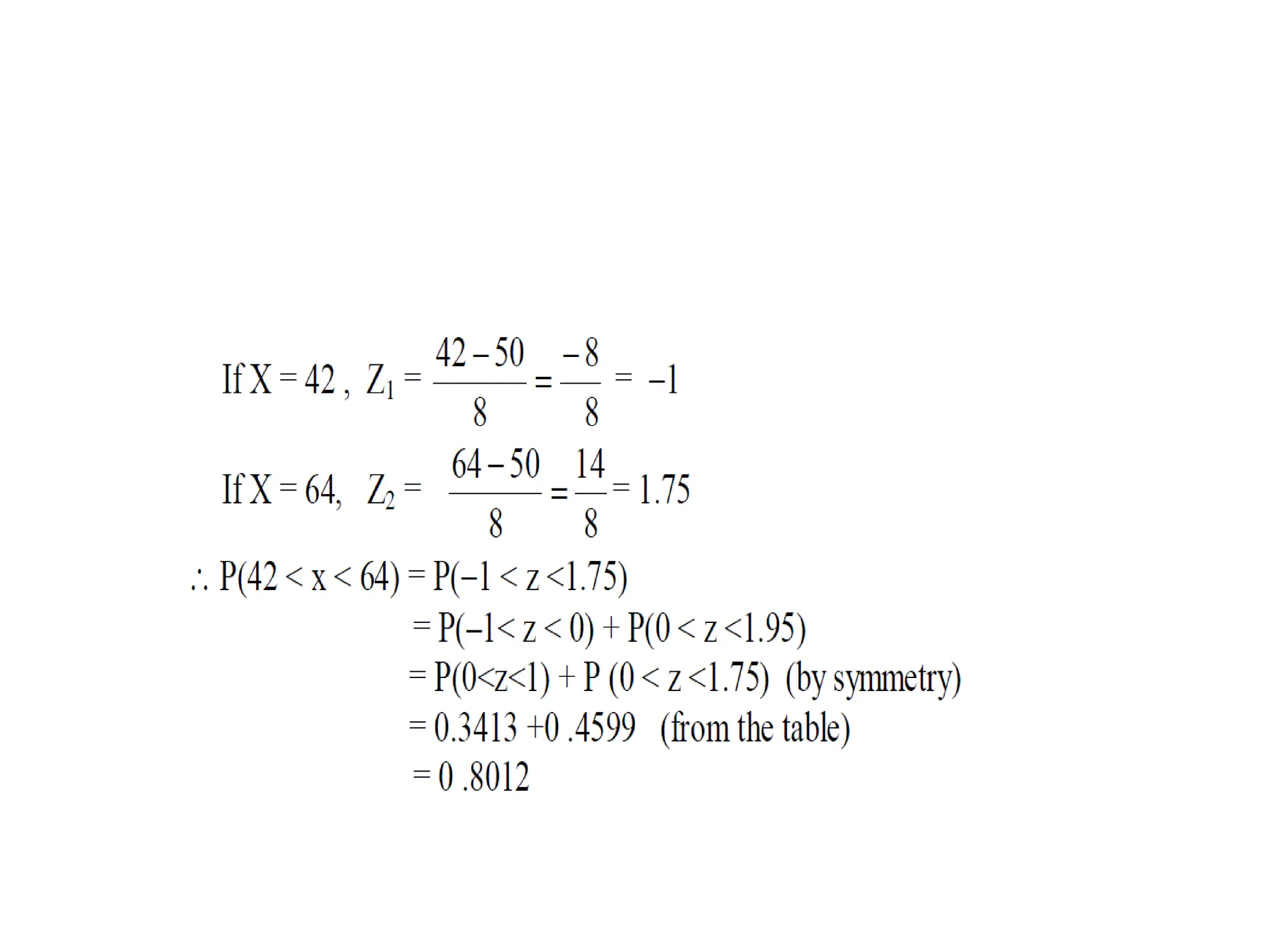
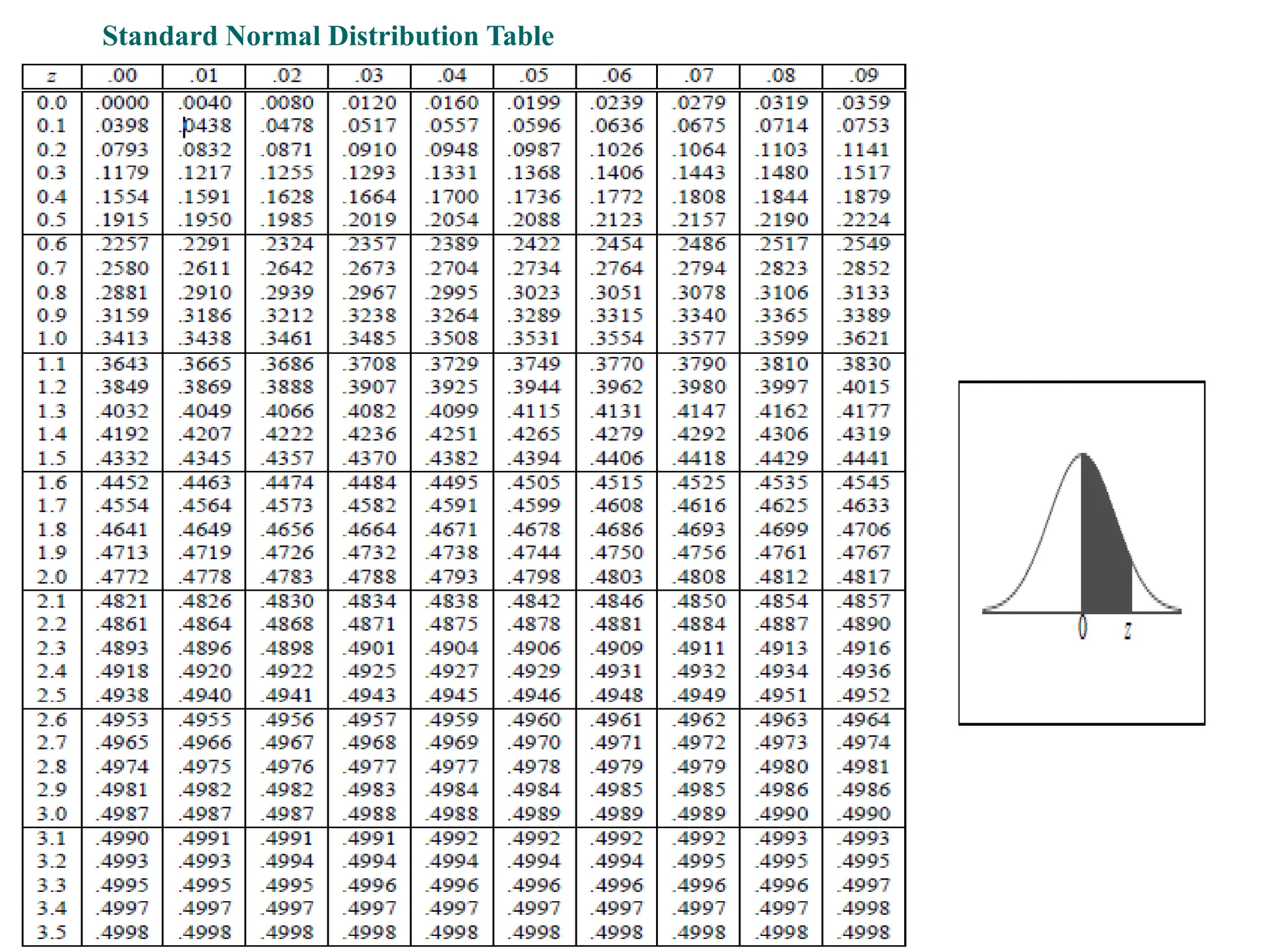
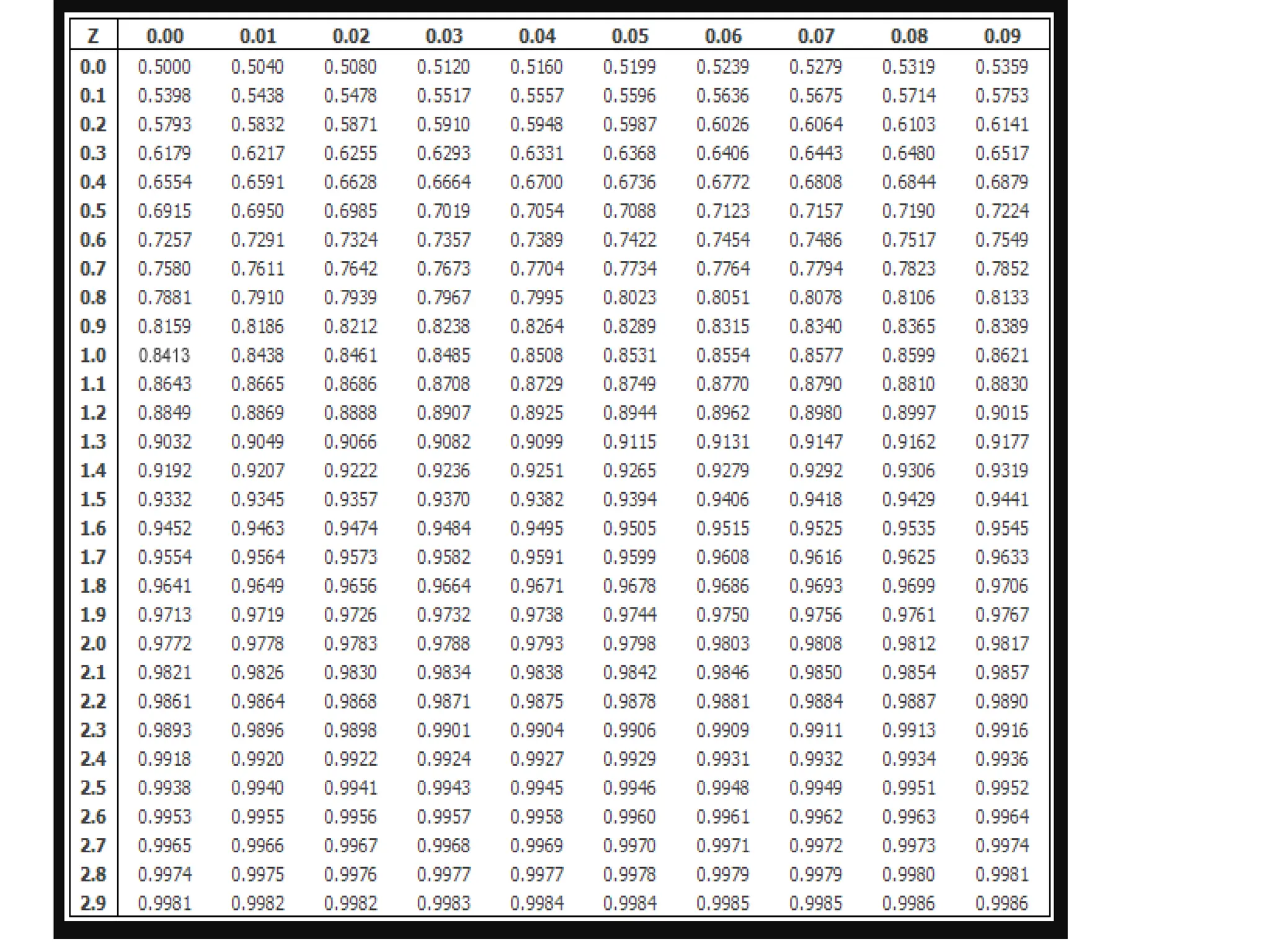
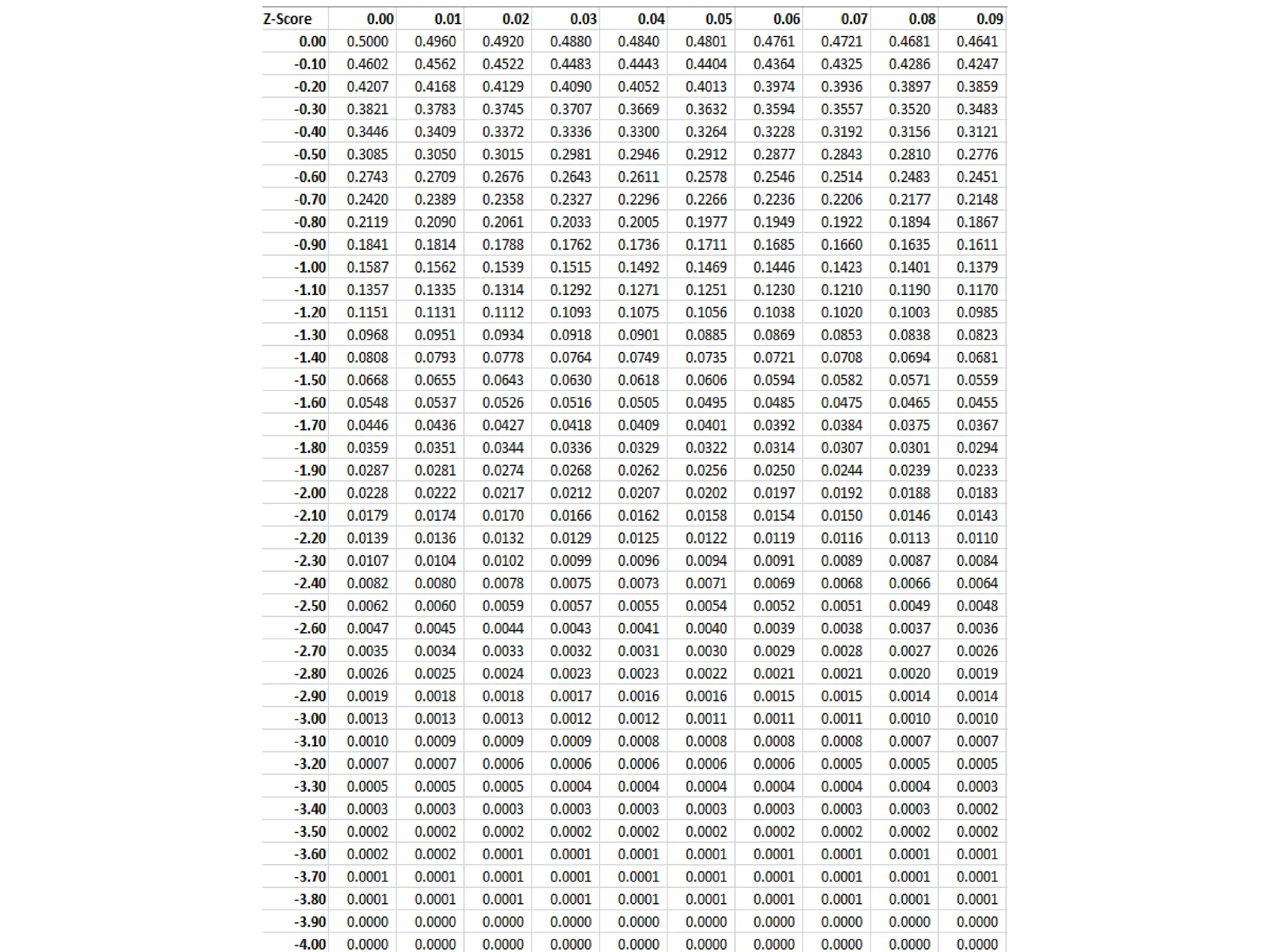
90. Activity 4. 1
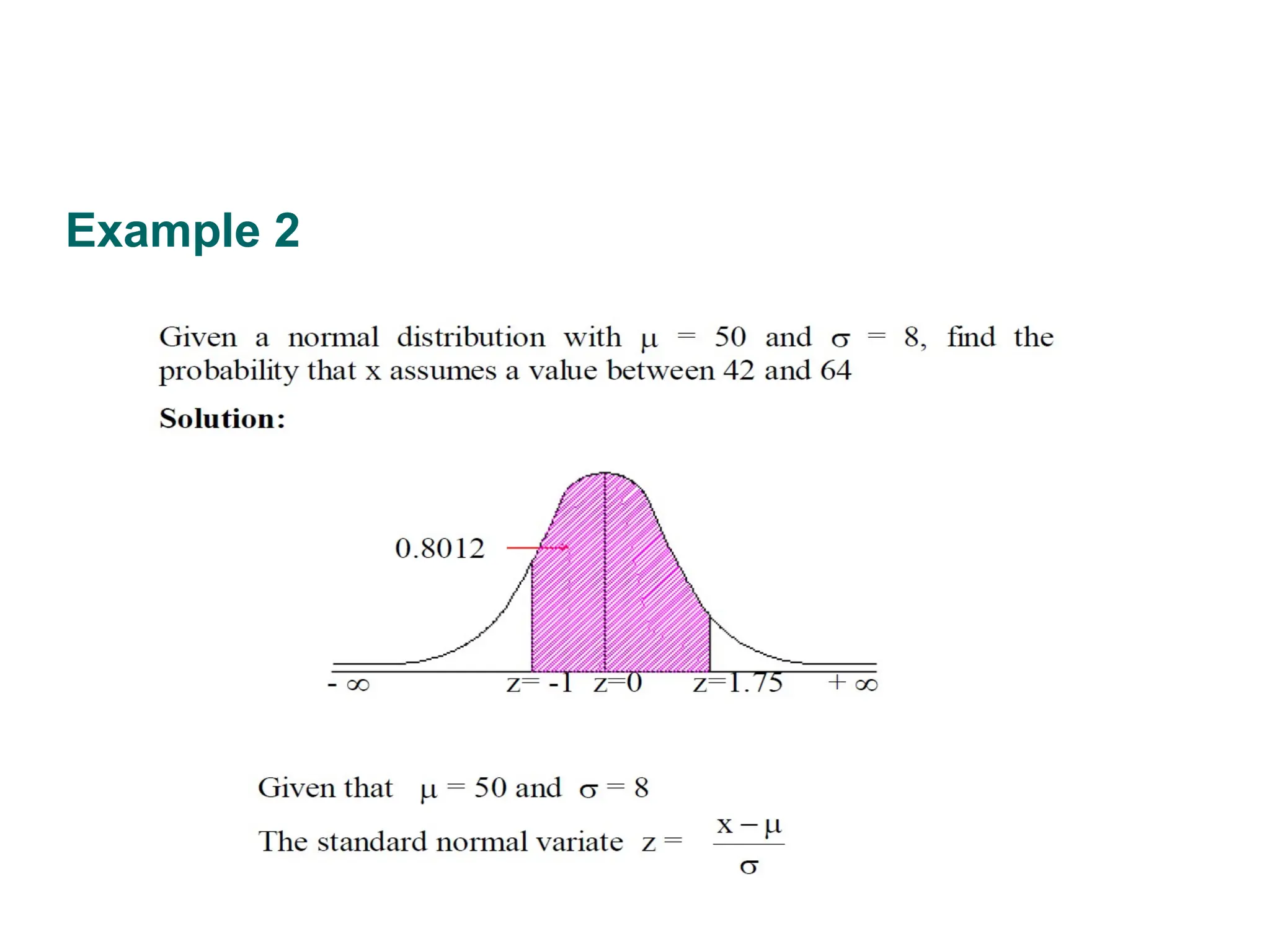
X is a normally normally distributed variable with mean μ = 30 and standard deviation σ = 4. Find
a) P(x < 40)
b) P(x > 21)
c) P(30 < x < 35)
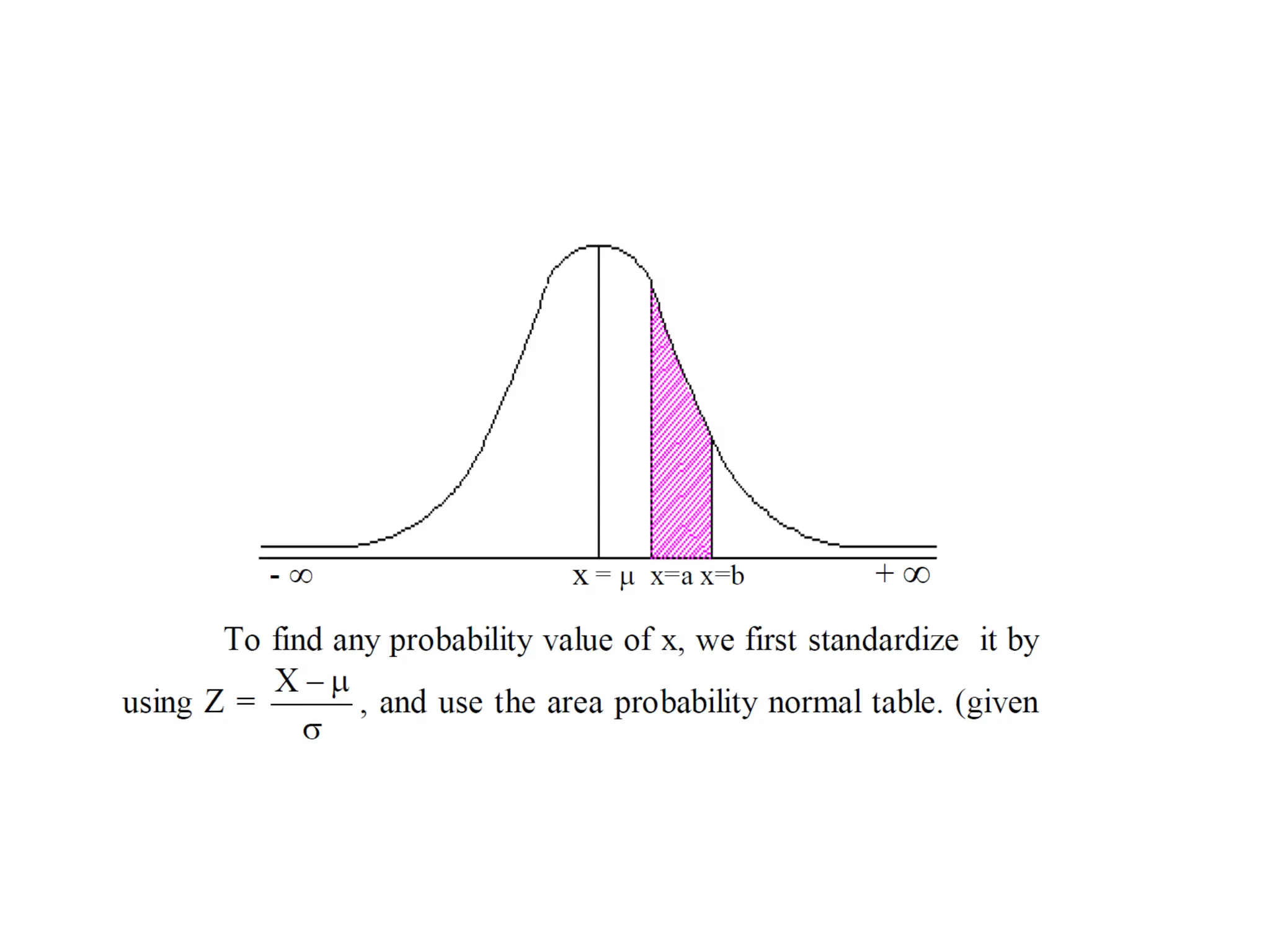
● Note: What is meant here by area is the area under the standard normal curve.
● Solution
a) For x = 40, the z-value z = (40 - 30) / 4 = 2.5
Hence P(x < 40) = P(z < 2.5) = [area to the left of 2.5] = 0.9938
b) For x = 21, z = (21 - 30) / 4 = -2.25
●
Hence P(x > 21) = P(z > -2.25) = [total area] - [area to the left of -2.25]
= 1 - 0.0122 = 0.9878
c) For x = 30 , z = (30 - 30) / 4 = 0 and for x = 35, z = (35 - 30) / 4 = 1.25
Hence P(30 < x < 35) = P(0 < z < 1.25) = [area to the left of z = 1.25] - [area to the left of 0]
= 0.8944 - 0.5 = 0.3944

91. Activity 4.2
● A radar unit is used to measure speeds of cars on a motorway. The speeds
are normally distributed with a mean of 90 km/hr and a standard deviation
of 10 km/hr. What is the probability that a car picked at random is travelling
at more than 100 km/hr?
● Solution
● Let x be the random variable that represents the speed of cars.
● x has μ = 90 and σ = 10. We have to find the probability that x is higher
than 100 or P(x > 100)
For x = 100 , z = (100 - 90) / 10 = 1
P(x > 90) = P(z > 1) = [total area] - [area to the left of z = 1]
= 1 - 0.8413 = 0.1587
The probability that a car selected at a random has a speed greater than 100
km/hr is equal to 0.1587

92. Activity 4.3
● For a certain type of computers, the length of time between
charges of the battery is normally distributed with a mean of 50
hours and a standard deviation of 15 hours. John owns one of
these computers and wants to know the probability that the length
of time will be between 50 and 70 hours.
● Solution
● Let x be the random variable that represents the length of time. It has a mean of 50 and a
standard deviation of 15. We have to find the probability that x is between 50 and 70 or
P( 50< x < 70)
For x = 50 , z = (50 - 50) / 15 = 0
For x = 70 , z = (70 - 50) / 15 = 1.33 (rounded to 2 decimal places)
P( 50< x < 70) = P( 0< z < 1.33) = [area to the left of z = 1.33] - [area to the left of z = 0]
= 0.9082 - 0.5 = 0.4082
The probability that John's computer has a length of time between 50 and 70 hours is equal to
0.4082.

93. Activity 4. 4
● Entry to a certain University is determined by a national test. The scores on this test are normally
distributed with a mean of 500 and a standard deviation of 100. Tom wants to be admitted to this
university and he knows that he must score better than at least 70% of the students who took the test.
Tom takes the test and scores 585. Will he be admitted to this university?
● Solution
● Let x be the random variable that represents the scores. x is normally ditsributed with a mean of 500
and a standard deviation of 100. The total area under the normal curve represents the total number of
students who took the test. If we multiply the values of the areas under the curve by 100, we obtain
percentages.
For x = 585 , z = (585 - 500) / 100 = 0.85
The proportion P of students who scored below 585 is given by
P = [area to the left of z = 0.85] = 0.8023 = 80.23%
Tom scored better than 80.23% of the students who took the test and he will be admitted to this
University.

94. Activity 4.5
● The annual salaries of employees in a large company are approximately
normally distributed with a mean of $50,000 and a standard deviation of
$20,000.
a) What percent of people earn less than $40,000?
b) What percent of people earn between $45,000 and $65,000?
c) What percent of people earn more than $70,000?
● Solution
a) For x = 40000, z = -0.5
Area to the left (less than) of z = -0.5 is equal to 0.3085 = 30.85% earning less than $40,000.
b) For x = 45000 , z = -0.25 and for x = 65000, z = 0.75
The area between z = -0.25 and z = 0.75 is equal to 0.3720 = 37.20 earn between $45,000 and
$65,000.
c) For x = 70000, z = 1
The area to the right (higher) of z = 1 is equal to 0.1586 = 15.86% earn more than $70,000.ing

95. Activity 4. 6
● The length of life of an instrument produced by a machine has a normal distribution with a
mean of 12 months and standard deviation of 2 months. Find the probability that an instrument
produced by this machine will last
a) less than 7 months.
b) between 7 and 12 months.
● Solution
● a) P(x < 7) = P(z < -2.5)
= 0.0062
b) P(7 < x < 12) = P(-2.5 < z < 0)
= 0.4938