Find the Formula Statistics Formulae for School Students by M. D. Raghu Ganit Learning Guides

1. FIND THE FORMULA
STATISTICS FORMULAE
FOR SCHOOL STUDENTS
M. D. Raghu
Ganit learning guides

2. Contents
1. Data spread, Central values.
2. Box and Whiskers diagram
3. Histogram
4. Probability rules
5 Tree diagram
6 Poisson probability
7. Binomial probability
8. Normal distribution curves
9. Standard normal distribution
10. Normal distribution table
11 Correlation
12 Regression line
13 Central limit theorem
14. Confidence interval and level
15. Confidence interval table
16. Expected value

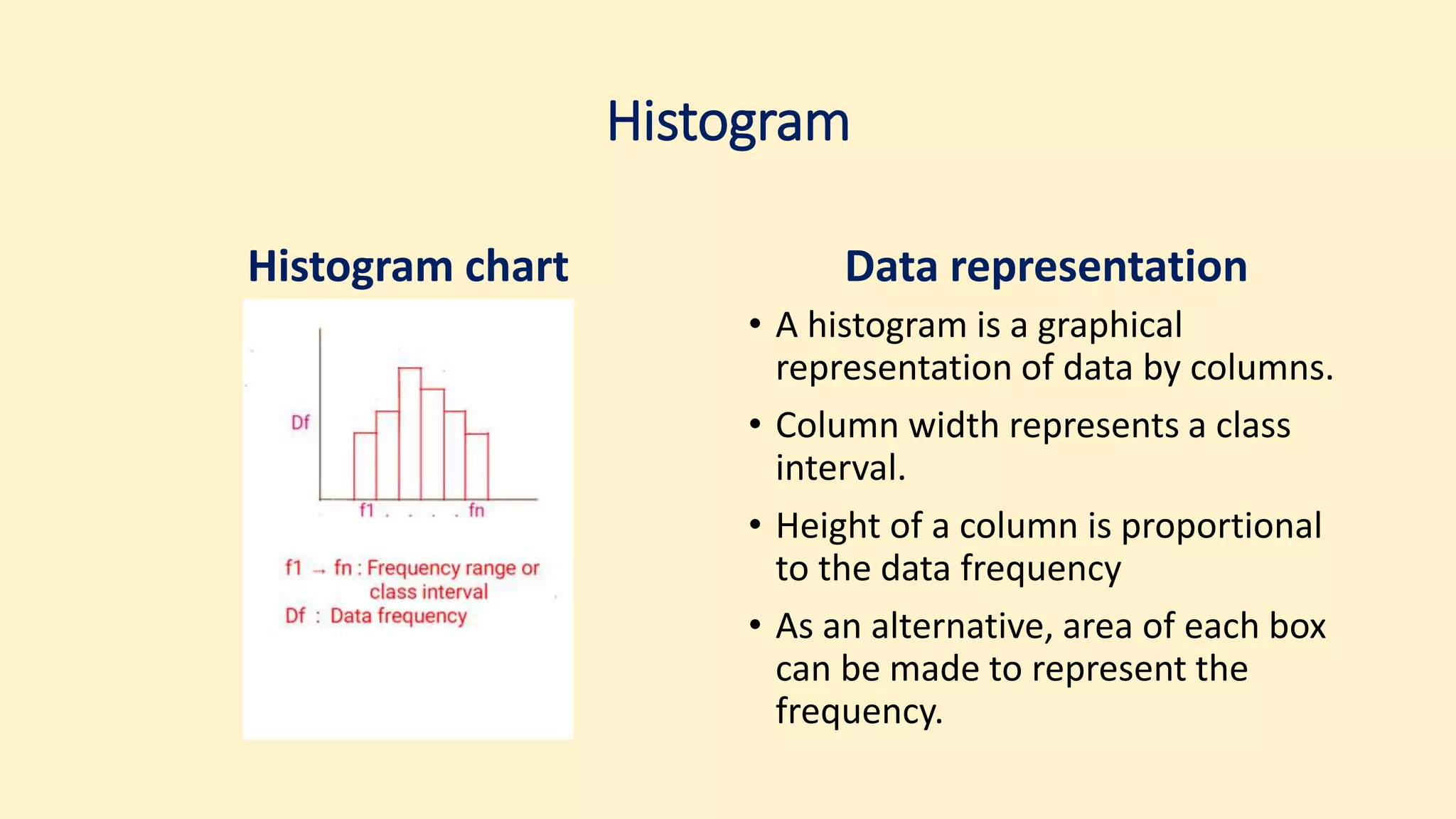
3. Data spread, Central values
Individual data spread
• Mean μ = ∑x/n
• Variance v = [∑(x−μ)²]/n
• Standard deviation ✓v = ✓σ = s
• Mode = Most common value.
• Median = Middle value
• n = Population size
Group data spread
Mean μ = ∑ (f×χ)/Σf
Population variance
. vₚ= ∑f×(χ – μ)²/∑f.
Standard deviation s = ✓vₚ
f = Class frequency
χ = Class mid-range
Σf = Total frequency

4. Box and whisker diagram
Box and whisker chart Chart properties
• A box plot represents data
divided into four quartiles.
• Difference between maximum
and minimum values are divided
into two whiskers and a box .
• Each whisker represents upper
or lower quartile and the box
inter quartile. A line within the
box shows the median.

5. Histogram
Histogram chart Data representation
• A histogram is a graphical
representation of data by columns.
• Column width represents a class
interval.
• Height of a column is proportional
to the data frequency
• As an alternative, area of each box
can be made to represent the
frequency.

6. Probability rules
P(A) = Probability of an event A
• P(A) is favourable outcomes to
total outcomes ratio
• P(A) = nf /nt.
• P(A’) is unfavorable outcomes to
total outcomes ratio.
• P(A) = 1-P(A’)
• If A and B are independent events
then probability of A or B is called
Probability of A union B.
•P(A∪B)=P(A)+P(B)
• If A and B are not independent
•P(A∪B)=P(A)+P(B)-P(A∩B)
• P(A∩B) is the occurrence of events
A and B together hence,
•P(A∩B)=P(A)•P(B given A).

7. Tree diagram
• Tree diagram is a simple
representation of probabilities.
• The branches show outcomes of
the first event followed by
outcomes of further events.
• Tree diagrams can be used for
both dependent and
independent events.
• Serial branches gives probability
combinations and diverging
branches gives probability sums.

8. Poisson probability distribution
Distribution probability Probability conditions
• Poisson distribution Is a discreet
probability of a number of
events over a specified interval.
• Interval is an unit such as time,
distance or number of people.
• λ is a relatively small number as
compared to the population
considered.

9. Binomial probability distribution
Probability function Binomial probability
• Binomial probability is for a distribution
that has only two types of outcomes.
• The probability that in n number of trials
there are r desired outcomes is given by
P(R).
• Probabilities of desired and undesired out
comes add up to 1.
• Binomial probability is a discrete
distribution.

10. Normal distribution curves
Bell shaped curve Normal distribution properties
Normal distribution is a bell shaped curve. This curve
follows Gaussian distribution pattern.
Measured statistical parameter, for example height of
students in a school, is shown on the X axis. Population
or Probability density is shown on Y axis.
Area under the entire curve covers the total population
or a Probability of 1.
Part of the curve gives the part of population in
between any two x values
Ratio of part of population between two x values to
the total population gives the Probability of a
parameter x given x₁<x<x₂ to be within x₁ and x₂ .
Normal distribution is a method for continuous data
Probability analysis.

11. Standard normal distribution
Bell shaped curve Normal probability distribution
X axis of a normal distribution curve gives
the population away from the mean. Area
under any part of the curve is a measure of
the population probability.
Standardised X axis represents Z score.
Percentage area under the curve for any
two Z scores gives the probability.
Z = (x −μ)/σ, σ=standard deviation, μ=mean
Y=Probability density=[e^(-z²/2)]/√(2π)

12. Standard normal distribution table
Normal distribution curve Z score vs. probability table
P(Z=Zn<Zn+1) % Probability
P(Z=-3<-2) 2.1
P (Z=-2<-1) 13.6
P(Z=-1<0) 34.1
P(Z=0<1) 34.1
P(Z=1<2) 13.6
P(Z=2<3) 2.1

13. Correlation
Regression factor r X and Y correlation
Correlation is a statistical relationship
between two sets of variables x and y.
Correlation or regression factor r is
calculated from the sets of variables
x,y and their means μx, μy.
r = ±1 indicates a strong correlation
between x and y and no correlation if
r = 0.

14. Regression line
Regression Line equation
Regression line is the best fit
line for a scatter plot.
r is the correlation factor.
Line equation:
y = mx + c where m = r(sᵧ/sₓ)
and
c= μᵧ - m(μₓ)
s is the standard deviation
and μ is the mean.
Regression Line graph

15. Central limit theorem
Central limit theorem is about samples of size ñ taken from a large
population n with mean μ and standard deviation s. The theorem is
valid for normal or any other type of distribution.
This theorem states that the distribution of the sample means x̅ will be
close to a normal distribution. x̅ is the mean of a sample set.
Mean μx̅ of the sample means will be equal to the mean μ of the
population. Standard deviation s̅ of the x̅ values will be equal to s/√ñ
The random samples are taken from the population, with
replacements. It should be sufficiently large. At least 30 or more
samples are required.

16. Confidence interval and level
Confidence interval is a range of
values that is likely to contain a
population parameter such as the
mean.
Confidence interval is expressed
as a range. If a parameter is
obtained from a sample survey
then the same parameter for the
population will probably lie with
in this range.
• Confidence level is the
percentage probability of a
population parameter to lie with
in a range of variation called
confidence interval.
• For example, consider average
scores of a sample group of
students. One can say with 90%
confidence level that the average
score of entire school students is
likely to be with in 50 to 80
marks confidence interval.

17. Confidence interval table
Confidence interval Ci
x̅+Z×s/✓n < μ < x̅−Z×s/✓n
μ = population mean
x̅ = sample means.
Z = z score for desired level (CL) of
μ as per CL versus Z table.
s = large sample or population
standard deviation
n = sample size
Margin of error = ±Z×(s/✓n)
Confidence percentage table
CL Z.
• 90%. 1.645
• 95%. 1.960
• 98%. 2.326
• 99%. 2.576.
• 99.9%. 3.291
• CL = Confidence level.

18. Expected value
Value function
E.V. = E(X) = Σx•P(X=x) = μ
σ = E(X²) – [E(X)]².
μ=mean, σ=standard deviation
If c and k are constants,
E(c+kX) = c + k(EX)
Expected value of x and w
E(X+W) = E(X)+ E(W)
Definition
• Expected value EV is the sum of
each possible outcome
multiplied by the probability of
each outcome.
• Expected value ‘EV’ is also the
mean value μ of the outcomes.
• Expected values of combination
of two variables Is the sum of
expected value of each variable.

19. GANIT LEARNING GUIDES
Thank you
M. D. Raghu
For mathematics and physics formulae
SlideShare.net/dhatiraghu