This document discusses key concepts in probability distributions including random variables, expected values, and common probability distributions such as binomial, hypergeometric, and Poisson. It provides examples and formulas for calculating mean, variance, and probability for each distribution. The key points are: - Random variables can take on numerical values determined by random experiments and can be discrete or continuous. 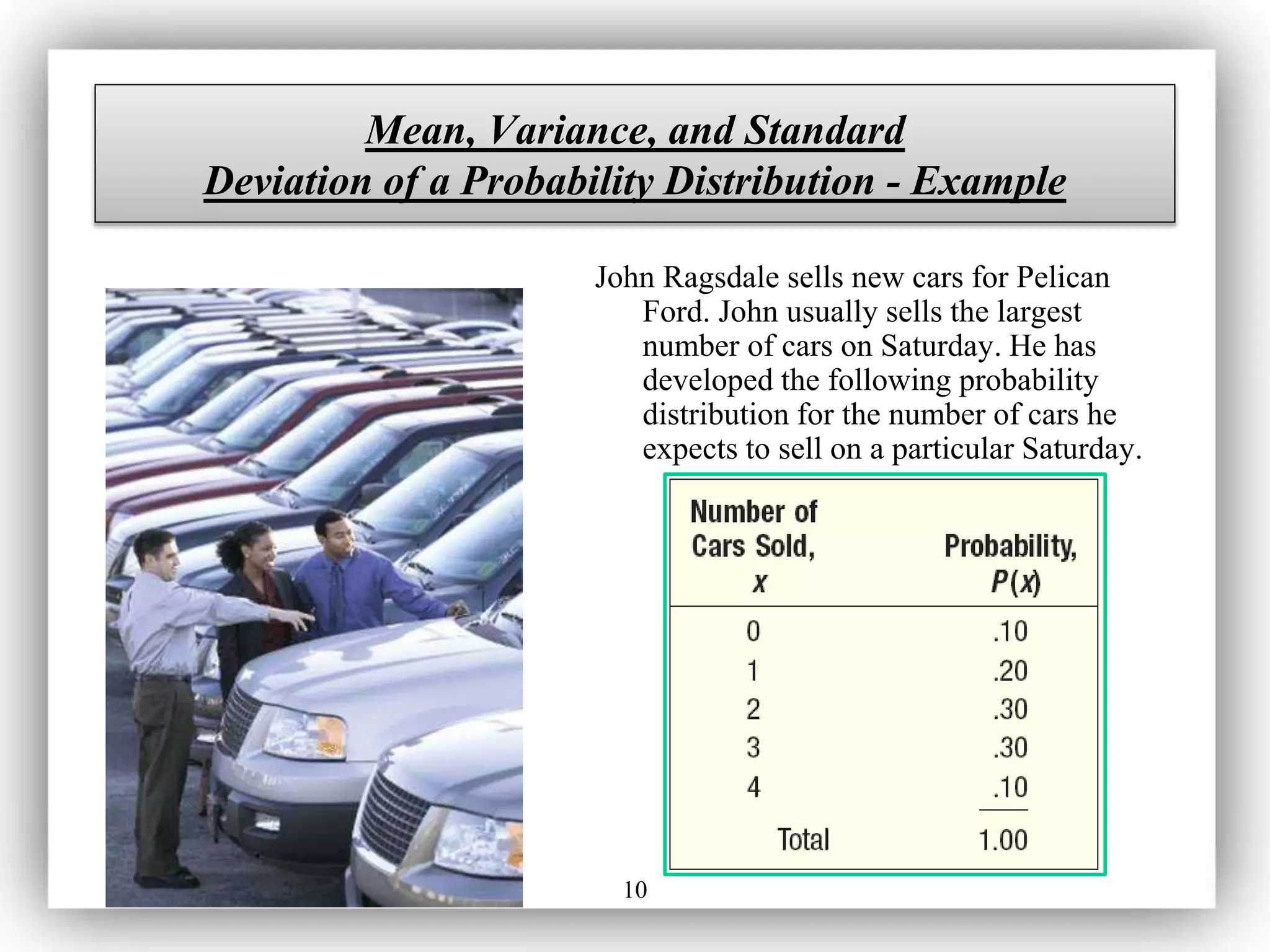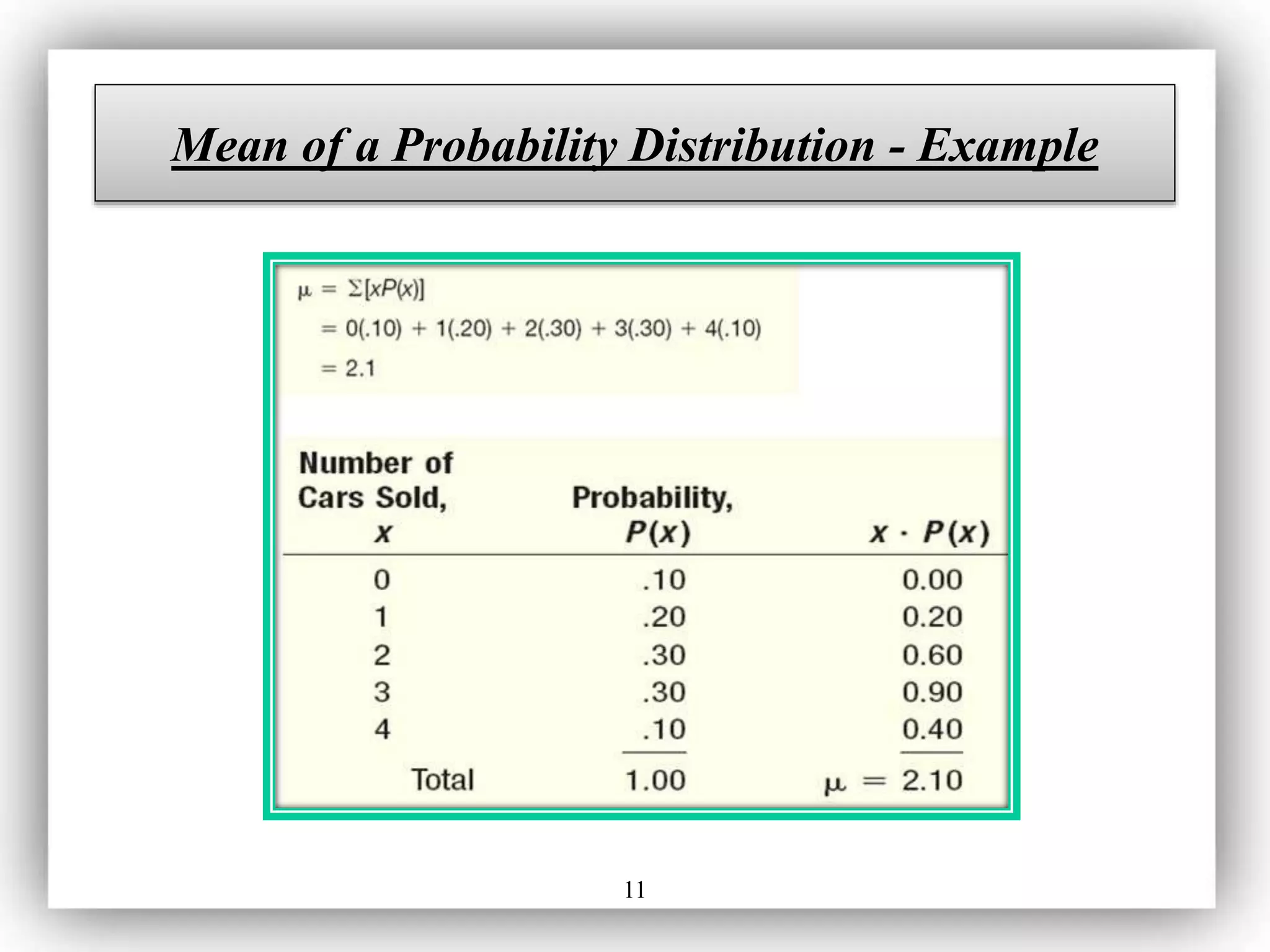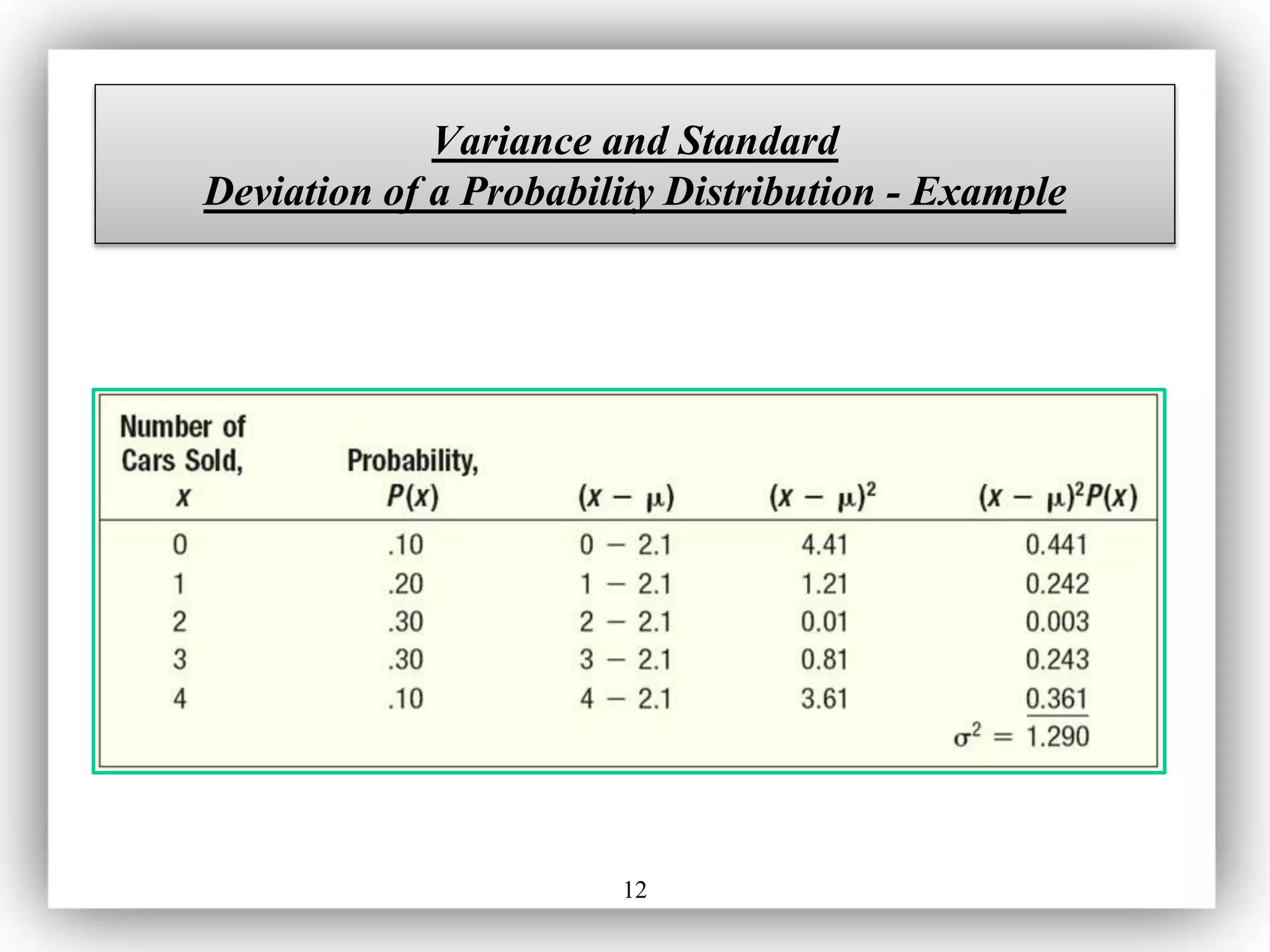- The expected value (mean) and variance characterize a probability distribution and the mean represents the central location or average value. 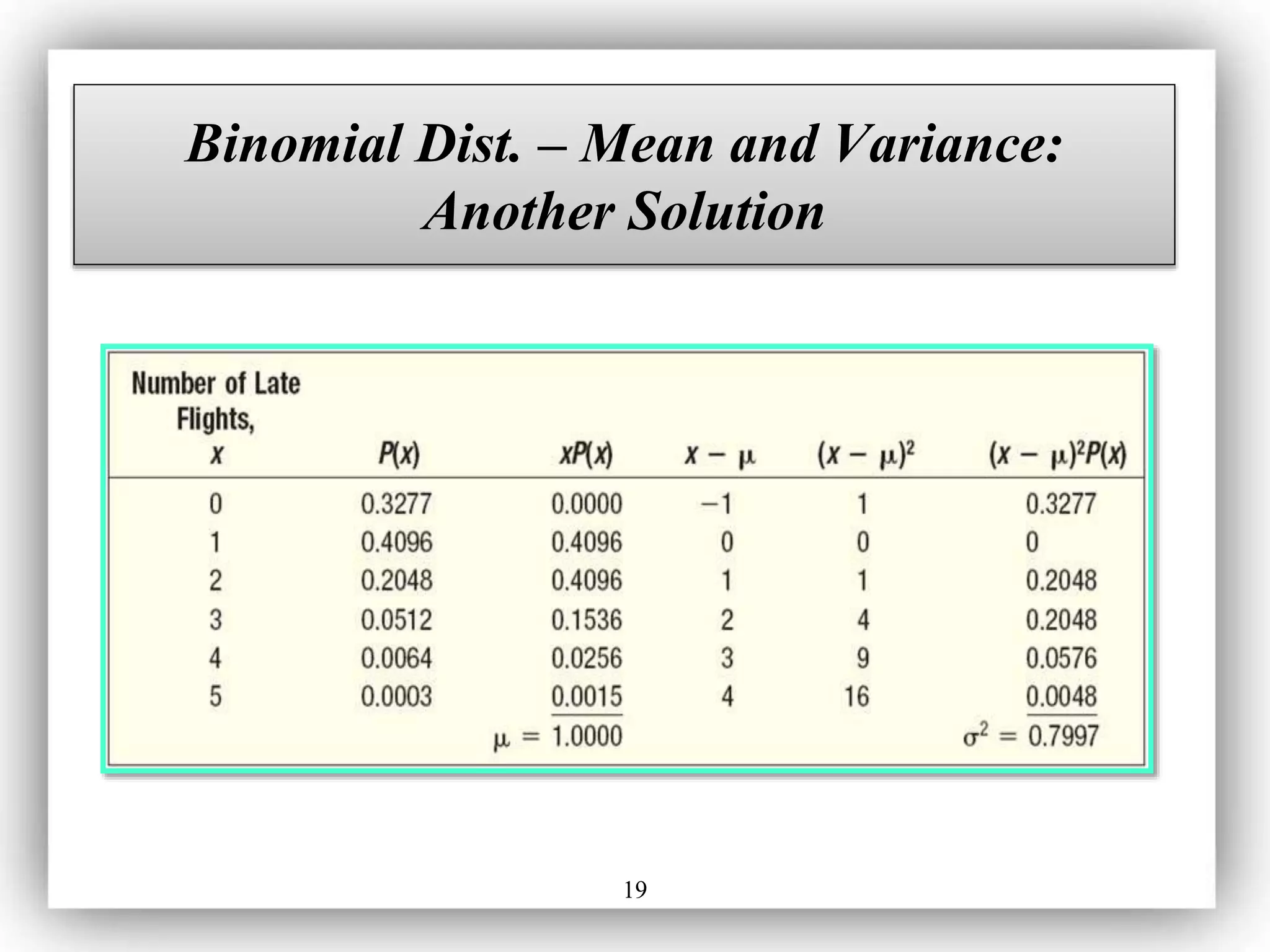- Common distributions include binomial for yes/no trials, hypergeometric for sampling without replacement, and Poisson for counting events over an interval. - Formulas are given for calculating probabilities, means, and variances for each distribution

1. Probability Distributions &
expected values

2. Probability
Probability is the study of randomness and
uncertainty
• Meaning
• Set
• Subset
• Random Experiment
• Mutually Exclusive Events
• Equally Like Events
• Sample Space

3. A random variable is a variable that
takes on numerical values
determined by the outcome of a
random experiment.
Random Variables

4. Discrete Random Variables
A discrete random variable is a random variable that
has values that has either a finite number of possible
values or a countable number of possible values. It is
usually the result of counting something
(Examples)
1. The number of students in a class.
2. Number of home mortgages approved by Coastal
Federal Bank last week.
3. The number of children in a family.
4. The number of cars entering a carwash in a hour

5. Continuous Random Variables
A continuous random variable is a random variable that
has an infinite number of possible values that is not
countable .It is usually the result of some type of
measurement
(Examples)
1. The income in a year for a family.
2. The distance students travel to class.
3. The time it takes an executive to drive to work.
4. The length of an afternoon nap.
5. The length of time of a particular phone call

6. Example: expected value
• Recall the following probability distribution of
ER arrivals:
x 10 11 12 13 14
P(x) .4 .2 .2 .1 .1


5
1
3.11)1(.14)1(.13)2(.12)2(.11)4(.10)(
i
i xpx

7. Expected Value and Variance
• All probability distributions
are characterized by an
expected value (mean) and a
variance (standard deviation
squared).

8. 8
The Mean of a Probability Distribution
MEAN
•The mean is a typical value used to represent the
central location of a probability distribution.
•The mean of a probability distribution is also
referred to as its expected value.

9. 9
The Variance, and Standard
Deviation of a Probability Distribution
Variance and Standard Deviation
• Measures the amount of spread in a distribution
• The computational steps are:
1. Subtract the mean from each value, and square this difference.
2. Multiply each squared difference by its probability.
3. Sum the resulting products to arrive at the variance.
The standard deviation is found by taking the positive square root
of the variance.

10. 10
Mean, Variance, and Standard
Deviation of a Probability Distribution - Example
John Ragsdale sells new cars for Pelican
Ford. John usually sells the largest
number of cars on Saturday. He has
developed the following probability
distribution for the number of cars he
expects to sell on a particular Saturday.

11. 11
Mean of a Probability Distribution - Example

12. 12
Variance and Standard
Deviation of a Probability Distribution - Example

13. The Binomial Distribution
The Bernoulli process is described by the binomial
probability distribution.
• The experiment consists of a sequence of n identical trials
•All possible outcomes can be classified into two categories,
usually called success and failure
•The probability of an success, p, is constant from trial to
trial
•The outcome of any trial is independent of the outcome of
any other trial

14. 14
Binomial Probability
Distribution
Characteristics of a Binomial Probability
Distribution
• There are only two possible outcomes on a
particular trial of an experiment.
• The outcomes are mutually exclusive,
• The random variable is the result of counts.
• Each trial is independent of any other trial

15. 15
Binomial Probability Formula

16. 16
Binomial Probability - Example
There are five flights
daily from Pittsburgh
via US Airways into the
Bradford, Pennsylvania,
Regional Airport.
Suppose the probability
that any flight arrives
late is .20.
What is the probability
that none of the flights
are late today?

17. 17
Binomial Dist. – Mean and Variance

18. 18
For the example regarding
the number of late
flights, recall that  =.20
and n = 5.
What is the average
number of late flights?
What is the variance of the
number of late flights?
Binomial Dist. – Mean and Variance:
Example

19. 19
Binomial Dist. – Mean and Variance:
Another Solution

20. Expected Value for
Binomial Probability
When an experiment meets the four
conditions of a binomial experiment
with n fixed trials and constant
probability of success p, the expected
value is:
E(x) = np

21. Hyper Geometric Distribution
The hyper geometric distribution has the
following characteristics:
• There are only 2 possible outcomes.
• The probability of a success is not the same
on each trial.
• It results from a count of the number of
successes in a fixed number of trials.

22. 22
Hyper geometric Distribution
Use the hyper geometric distribution to
find the probability of a specified
number of successes or failures if:
– the sample is selected from a finite
population without replacement
– the size of the sample n is greater than
5% of the size of the population N (i.e.
n/N  .05)

23. 23
Hyper geometric Distribution

24. 24
Hyper geometric Distribution - Example
Playtime Toys, Inc., employs 50
people in the Assembly
Department. Forty of the
employees belong to a union
and ten do not. Five employees
are selected at random to form
a committee to meet with
management regarding shift
starting times. What is the
probability that four of the five
selected for the committee
belong to a union?

25. 25
Hyper geometric Distribution - Example

26. • Mean
= n(k/N)
• Variance
= npq(N-n/N-1)
Hyper geometric Distribution

27. Poisson Distribution
The Poisson probability distribution describes the
number of times some event occurs during a
specified interval. The interval may be time,
distance, area, or volume.
• Assumptions of the Poisson Distribution
(1)The probability is proportional to the length of
the interval.
(2)The intervals are independent.

28. 28
Poisson Probability Distribution
The Poisson distribution can be described
mathematically using the formula:

29. 29
Assume baggage is rarely lost by Northwest
Airlines. Suppose a random sample of 1,000
flights shows a total of 300 bags were lost.
Thus, the arithmetic mean number of lost bags
per flight is 0.3 (300/1,000). If the number of
lost bags per flight follows a Poisson
distribution with u = 0.3, find the probability
of not losing any bags.
Poisson Probability Distribution - Example

30. 30
Poisson Probability Distribution
• The mean number of successes 
can be determined in binomial
situations by n, where n is the
number of trials and  the probability
of a success.
• The variance of the Poisson
distribution is also equal to n .

31. EXPECTED VALUE
Suppose the random variable x can
take on the n values x1, x2, …, xn.
Also, suppose the probabilities that
these values occur are respectively p1,
p2, …, pn. Then the expected value of
the random variable is:
E(x) = x1p1 + x2p2 + …. + xnpn

32. Example
X 1 2 3 4 5
P(x) .13 .29 .38 .13 .08
Find the expected value of x in the probability
distribution below: