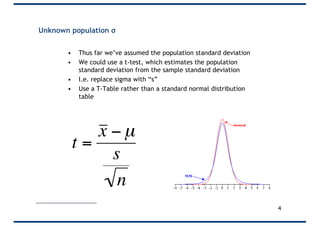
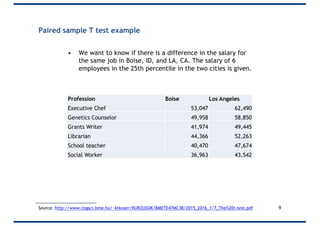
The document discusses Student's t-test, which is useful for three situations: when sample sizes are small, when the population standard deviation is unknown, and when comparing two samples. It describes how Student's t-test addresses the problems with small sample sizes that violate the Central Limit Theorem. It also explains how the t-test can be used to estimate an unknown population standard deviation from the sample standard deviation. Finally, it provides examples of using a t-test to compare the means of two samples and of using a paired t-test to compare salaries between two cities for the same jobs.

1. Student’s T Test
Anthony J. Evans
Professor of Economics, ESCP Europe
www.anthonyjevans.com
(cc) Anthony J. Evans 2019 | http://creativecommons.org/licenses/by-nc-sa/3.0/

2. Student’s T-test is useful in three situations
1. Low sample size
2. Unknown population standard deviation
3. Comparing two samples
2

3. Low sample size
• Use a z test to replicate a normal distribution
• But if the sample size is small, the Central Limit Theorem
doesn’t hold
• Use a t test (i.e. involve degrees of freedom)
– DoF: is a measure of the number of independent pieces
of information on which the precision of a parameter
estimate is based.
• William Gosset was hired by Guinness after graduating from
Oxford University
• Used statistics to find best yielding varieties of barley
• Problem: small samples
• To keep trade secrets he published under the pseudonym
“Student”
• Hence “Student’s t-Test”
3

4. Unknown population σ
• Thus far we’ve assumed the population standard deviation
• We could use a t-test, which estimates the population
standard deviation from the sample standard deviation
• I.e. replace sigma with “s”
• Use a T-Table rather than a standard normal distribution
table
4
t =
x − µ
s
n

5. Comparing two samples
• We can also use the t-test to see whether the means of
two samples are statistically different from one another
• Once you compute the t-value you have to look it up in a
table of significance to test whether the ratio is large
enough to say that the difference between the groups is
not likely to have been a chance finding
• P-Value
– Usually use 0.5
• Degrees of Freedom
– The sample size of both groups combined, minus 2
5
𝑡 =
𝑥 𝑎% − 𝑥 𝑏%
𝑠 𝑎
2
𝑛 𝑎
+
𝑠 𝑏
2
𝑛 𝑏

6. Z test vs. T test
6
€
z =
x − µ0
σ
n
€
t =
x − µ0
s
n
Degrees of Freedom = n-1
For comparing 2 samples = n-2
Student’s T test
• Used when you only know the
standard deviation of a sample
(s)
• Used if small sample size
• Can also be used for comparing
two samples
Z test
• Used when you know the
standard deviation of the
population (σ)
𝑡 =
𝑥 𝑎% − 𝑥 𝑏%
𝑠 𝑎
2
𝑛 𝑎
+
𝑠 𝑏
2
𝑛 𝑏

7. Unpaired sample T test example
• Rosenthal and Jacobson (1968) informed classroom
teachers that some of their students showed unusual
potential for intellectual gains. Eight months later the
students identified to teachers as having potential for
unusual intellectual gains showed significantly greater gains
performance on a test said to measure IQ than did children
who were not so identified. Below are the data for the
students in the first grade:
7Source: http://www.indiana.edu/~educy520/sec6342/week_10/ttest_exp.pdf

8. Unpaired sample T test example
• Calculate the T stat
• Find the critical value
• Do we reject the null hypothesis?
• Yes - the difference in scores is not due
to chance variation
8Source: http://www.indiana.edu/~educy520/sec6342/week_10/ttest_exp.pdf
𝑡 =
27.15 − 11.95
12.52
20
+
14.62
20
=
3.54
𝑡0.05, 38 = 2.03

9. Paired sample T test example
• We want to know if there is a difference in the salary for
the same job in Boise, ID, and LA, CA. The salary of 6
employees in the 25th percentile in the two cities is given.
9Source: http://www.cogsci.bme.hu/~ktkuser/KURZUSOK/BMETE47MC38/2015_2016_1/7_The%20t-test.pdf
Profession Boise Los Angeles
Executive Chef 53,047 62,490
Genetics Counselor 49,958 58,850
Grants Writer 41,974 49,445
Librarian 44,366 52,263
School teacher 40,470 47,674
Social Worker 36,963 43,542

10. 10Source: http://www.cogsci.bme.hu/~ktkuser/KURZUSOK/BMETE47MC38/2015_2016_1/7_The%20t-test.pdf

11. Solutions
11

12. Unpaired sample T test example
• Calculate the T stat
• Find the critical value
• Do we reject the null hypothesis?
• Yes - the difference in scores is not due
to chance variation
12Source: http://www.indiana.edu/~educy520/sec6342/week_10/ttest_exp.pdf
𝑡 =
27.15 − 11.95
12.52
20
+
14.62
20
=
3.54
𝑡0.05, 38 = 2.03

13. • This presentation forms part of a free, online course
on analytics
• http://econ.anthonyjevans.com/courses/analytics/
13