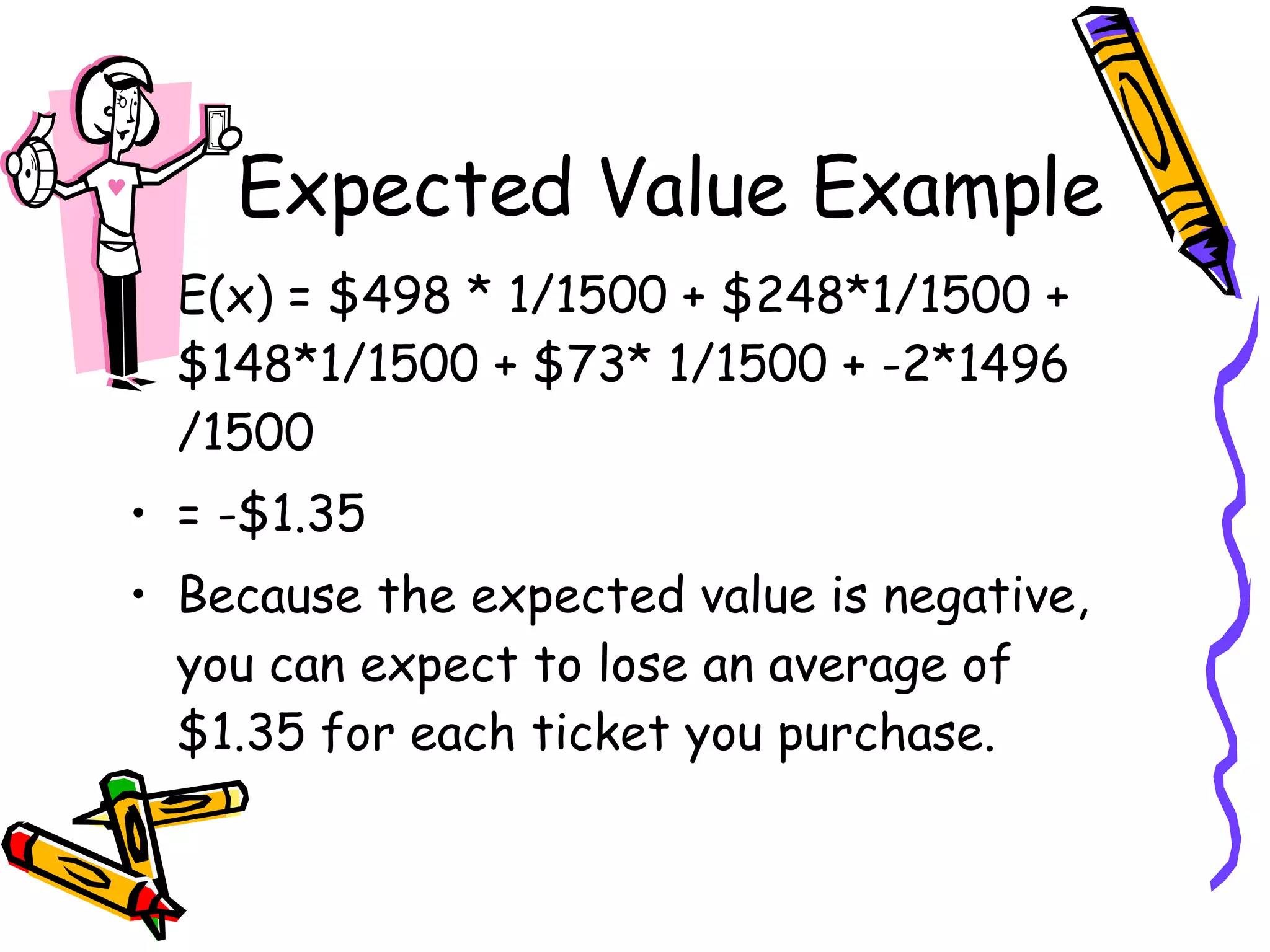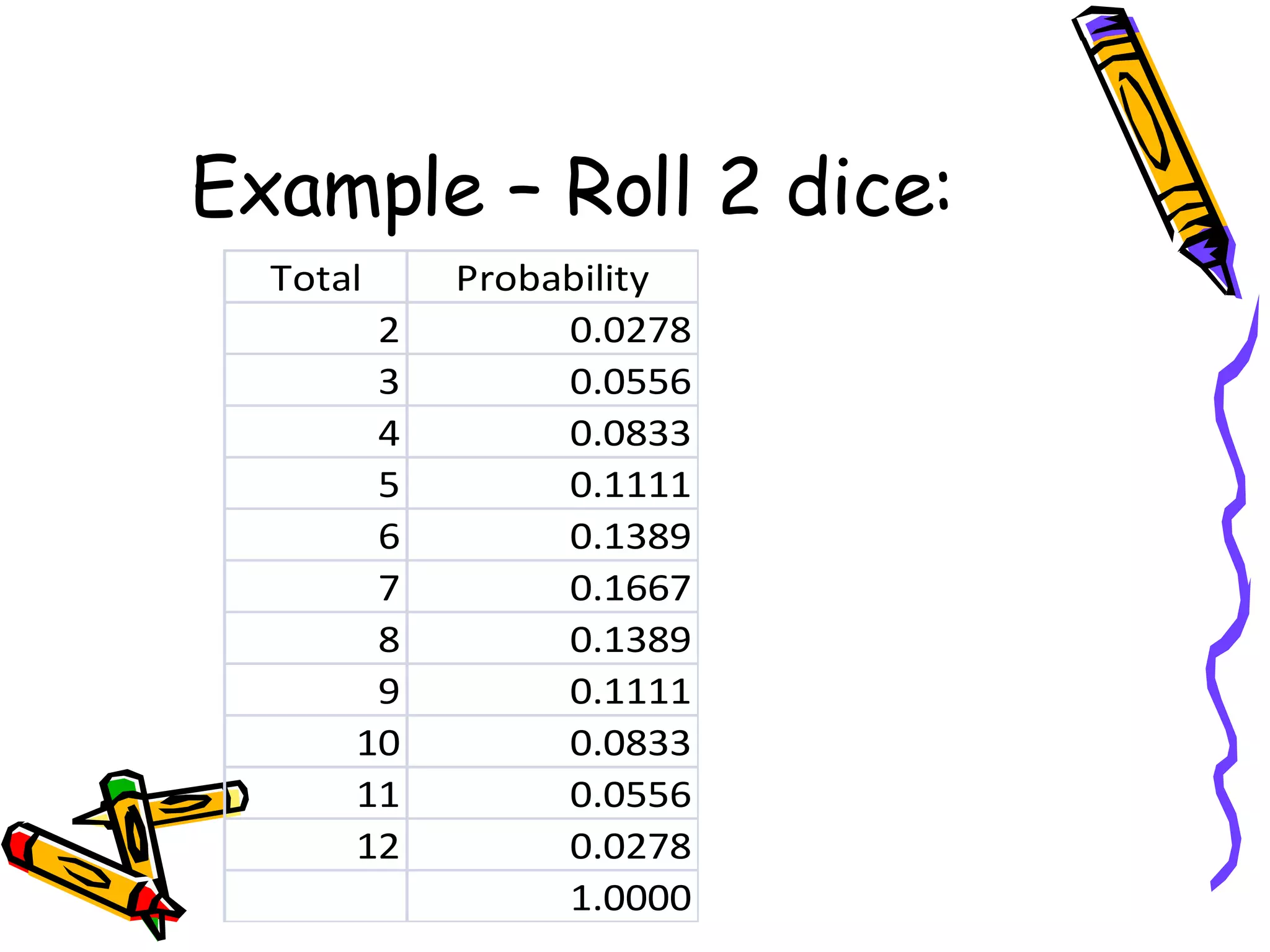
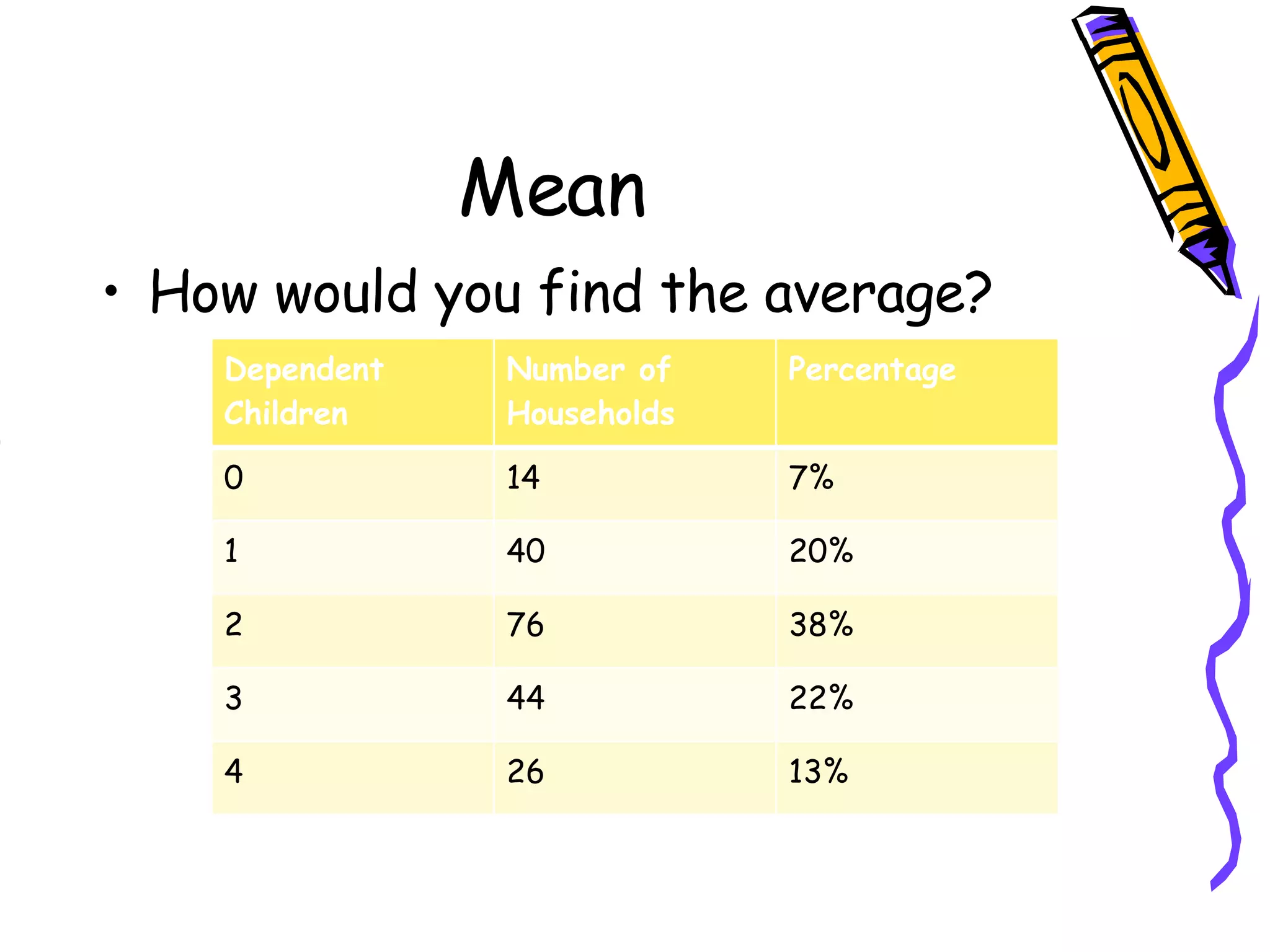
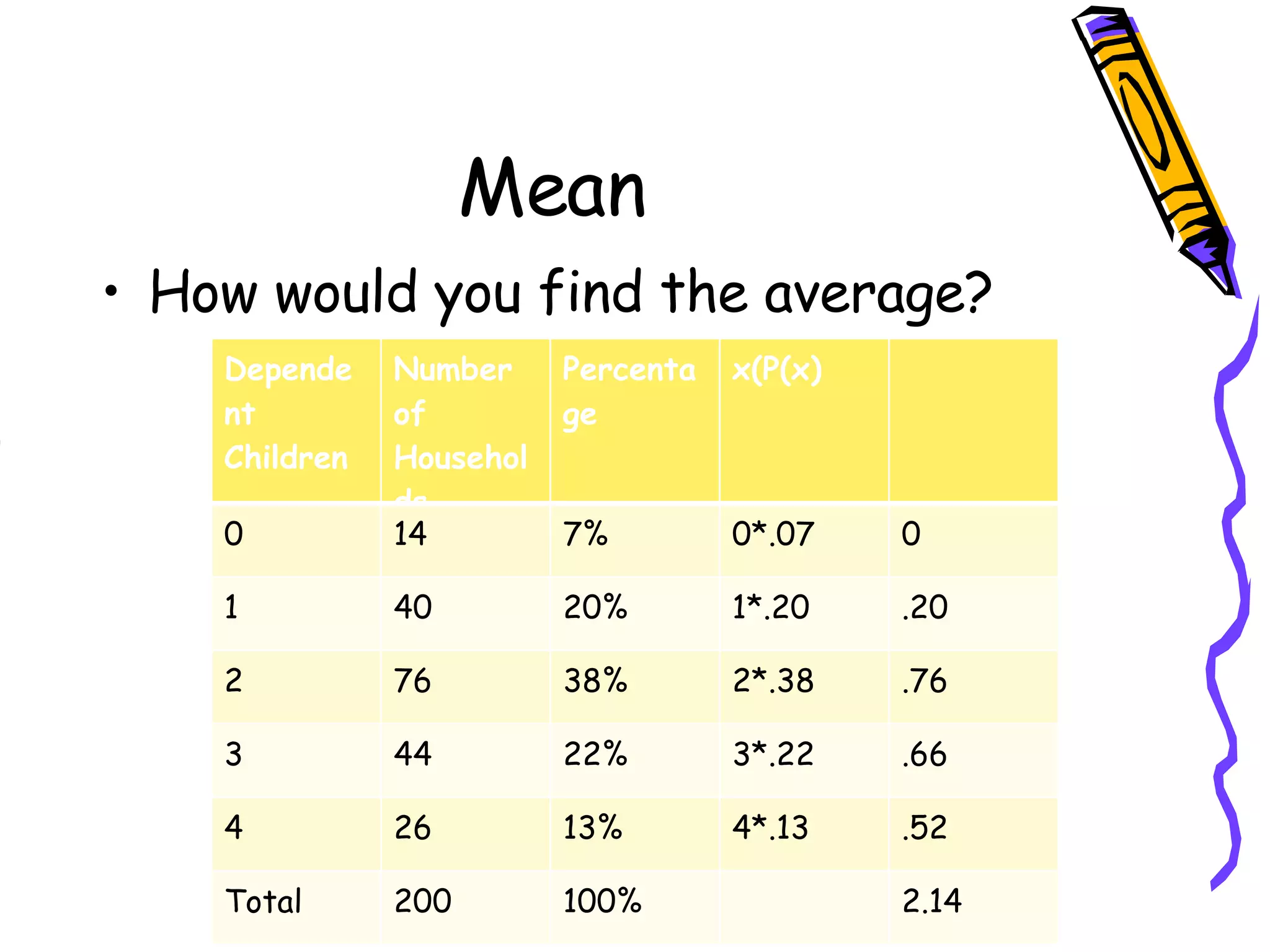
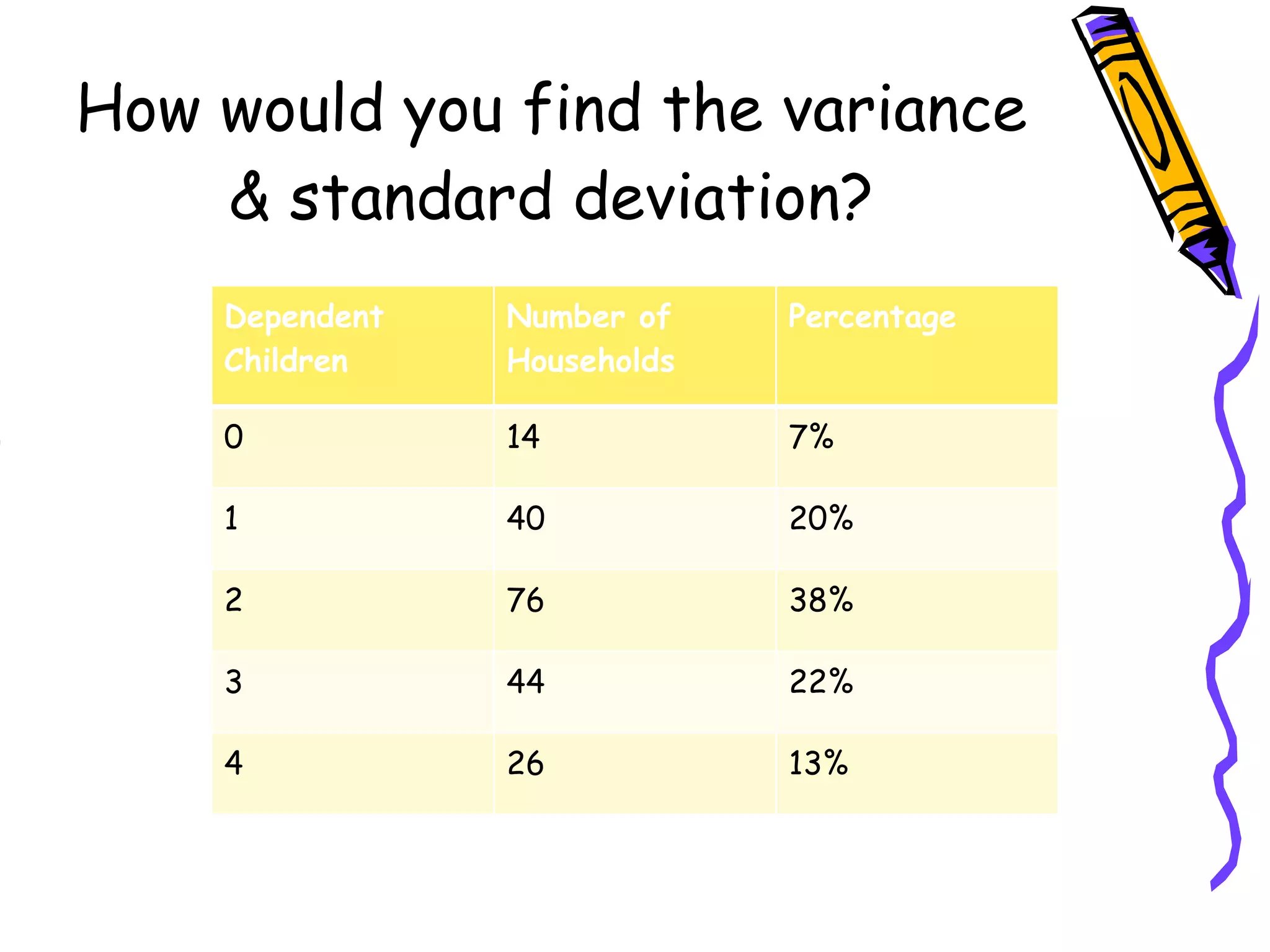
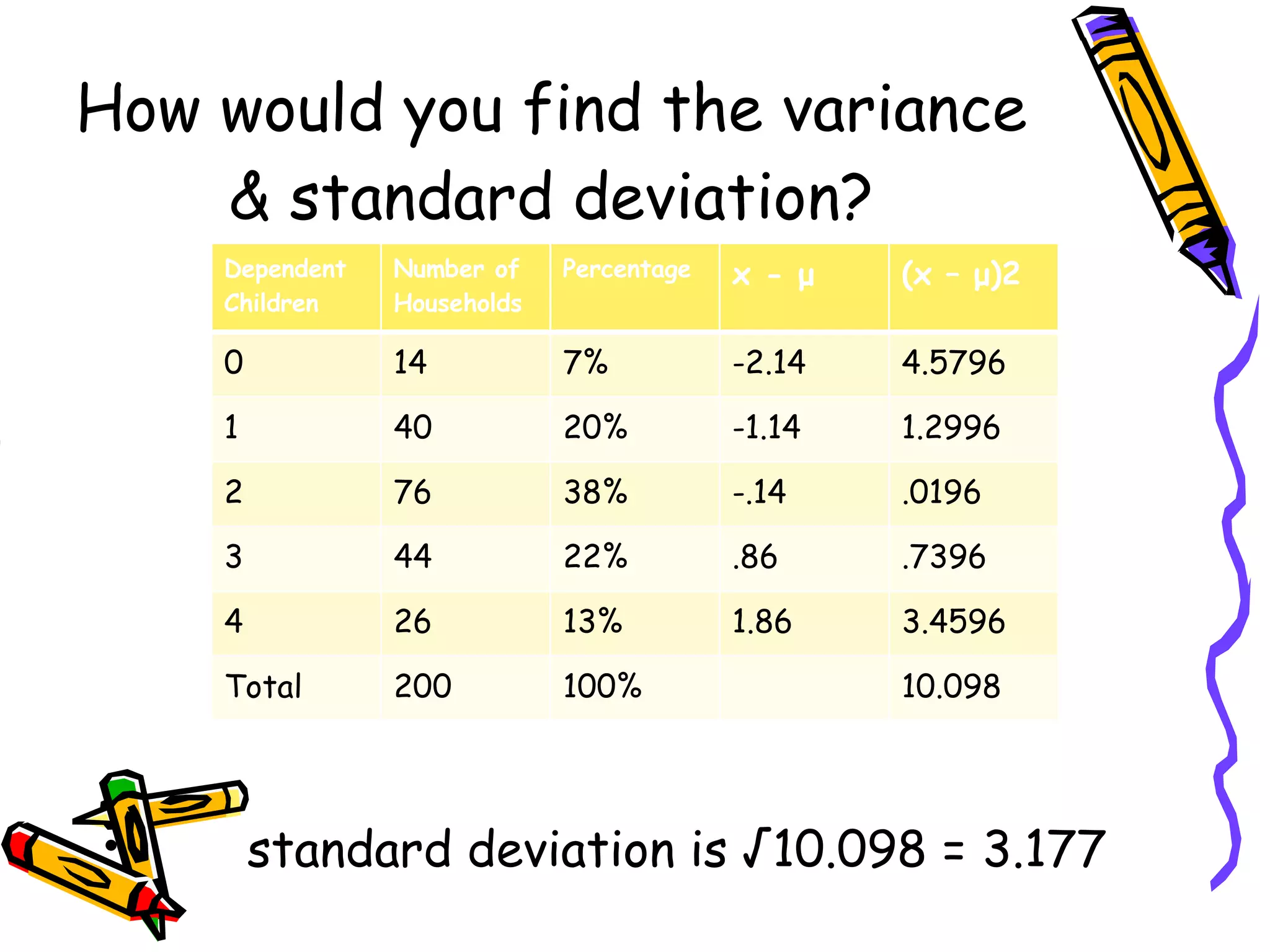
This document discusses probability distributions and key concepts related to discrete random variables including: - Distinguishing between discrete and continuous random variables - Constructing a discrete probability distribution from sample data and calculating probabilities - Finding the mean, variance, and standard deviation of a discrete probability distribution - Calculating the expected value of a discrete random variable from its possible outcomes and probabilities

1. Probability Distributions Chapter 4.1

2. Objectives Distinguish between discrete random variables and continuous random variables Learn to construct a discrete probability distribution and its graph Learn to find the mean, variance, and standard deviation of a discrete probability distribution Learn to find the expected value of a discrete probability distribution

3. Discrete & Continuous Discrete data is countable Number of students Number of sales calls Continuous data has an infinite number of possible outcomes Amount of time Temperature

4. Random Variables A random variable x represents a numerical value associated with each outcome of a probability experiment. The random variable is discrete if it has a finite or countable number of possible outcomes that can be listed. The variable is continuous if it has an uncountable number of possible outcomes, represented by an interval on the number line.

5. Discrete or Continuous? The number of stocks in the Dow Jones Industrial Average that have a share price increase on a given day.

6. Discrete or Continuous? The length of time it takes to complete a test.

7. Discrete or Continuous? The number of home runs hit during a baseball game

8. Discrete Probability Distributions A discrete probability distribution lists each possible value the random variable can assume, together with its probability. The Rules: The probability of each value is between 0 and 1. The sum of all the probabilities is 1.

9. Example – Roll 2 dice:

10. Constructing a Discrete Probability Distribution Let x be a discrete random variable with the possible outcomes x 1 , x 2 , . . . x n Make a frequency distribution for the possible outcomes. Find the sum of the frequencies. Find the probability of each possible outcome by dividing its frequency by the sum of the frequencies. Check that each probability is between 0 and 1 and that the sum is 1.

11. Example A sociologist surveyed 200 households in a small town and asked how many dependents they had. The results were: Dependent Children Number of Households 0 14 1 40 2 76 3 44 4 26

12. Example Find the sum of the frequencies: 200 Find the probability of each possible outcome: Dependent Children Number of Households Percentage 0 14 7% 1 40 20% 2 76 38% 3 44 22% 4 26 13%

13. Example Check that each probability is between 0 and 1 and that the sum is 1 Dependent Children Number of Households Percentage 0 14 7% 1 40 20% 2 76 38% 3 44 22% 4 26 13%

14. Mean How would you find the average? Dependent Children Number of Households Percentage 0 14 7% 1 40 20% 2 76 38% 3 44 22% 4 26 13%

15. Mean How would you find the average? Dependent Children Number of Households Percentage x(P(x) 0 14 7% 0*.07 0 1 40 20% 1*.20 .20 2 76 38% 2*.38 .76 3 44 22% 3*.22 .66 4 26 13% 4*.13 .52 Total 200 100% 2.14

16. Mean The mean of a discrete random variable is given by: μ = ∑xP(x) Each value of x is multiplied by its corresponding probability and the products are added.

17. How would you find the variance & standard deviation? Dependent Children Number of Households Percentage 0 14 7% 1 40 20% 2 76 38% 3 44 22% 4 26 13%

18. How would you find the variance & standard deviation? standard deviation is √10.098 = 3.177 Dependent Children Number of Households Percentage x - μ (x – μ )2 0 14 7% -2.14 4.5796 1 40 20% -1.14 1.2996 2 76 38% -.14 .0196 3 44 22% .86 .7396 4 26 13% 1.86 3.4596 Total 200 100% 10.098

19. Mean, Variance, & Standard Deviation The variance of a discrete random variable is given by: σ 2 = ∑(x- μ ) 2 P(x) A shortcut of this formula is: σ 2 = ∑x 2 P(x) - μ 2 The standard deviation is: σ = √ σ 2

20. Expected Value The expected value of a discrete random variable is equal to the mean of the random variable.

21. Expected Value Example At a raffle, 1500 tickets are sold at $2 each for 4 prizes of $500, $250, $150, and $75. You buy 1 ticket. What is the expected value of your gain? What are your possible gains? $500-$2 = $498 $248, $148, $73, and $-2 What is the possibility of each of these? 1/1500 for the first 4, 1496/1500 for the -2

22. Expected Value Example E(x) = $498 * 1/1500 + $248*1/1500 + $148*1/1500 + $73* 1/1500 + -2*1496/1500 = -$1.35 Because the expected value is negative, you can expect to lose an average of $1.35 for each ticket you purchase.

23. Homework P. 179 Do 1-10 together P. 179 12-28, 34 evens