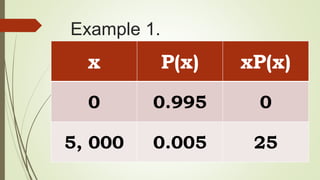
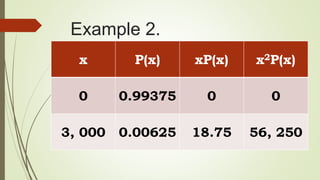
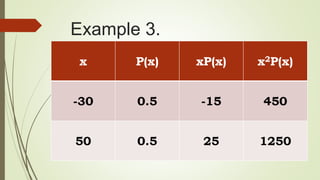
The document discusses the concepts of mean, variance, and standard deviation related to discrete random variables. It provides formulas for calculating expected values and variance, along with several examples illustrating these concepts in practical scenarios. The document also touches on the interpretation of variance and how standard deviation provides a more relatable measure due to using the same units as the variable.

1. Mean, Variance, and
Standard Deviation of a
Discrete Random
Variable
mhaykhel_3001

2. Mean or Expected
ValueIt is the weighted average of all the
values that the random variable X would
assume in the long run.
The discrete random variable X assumes
values or outcomes in every trial of an
experiment with their corresponding
probabilities.

3. Mean or Expected
ValueE(X) = ∑[xP(x)], where
X = discrete random variable
x = outcome or value of the
random variable
P(x) = probability of the
outcome x

4. Example 1
A researcher surveyed the households in a
small town. The random variable X represents
the number of college graduates in the
households. The probability distribution of X is
shown below:
Find the mean or expected value of X.
x 0 1 2
P(X) 0.25 0.50 0.25

5. Example 1 Solution
The expected value is 1. So the average
number of college graduates in the
household of the small town is one.
x P(x) xP(x)
0 0.25 0.00
1 0.50 0.50
2 0.25 0.50
∑[xP(x)] = 1.00

6. Example 2
A random variable X has this probability
distribution:
Calculate the expected value of X.
x 0 1 2
P(X) 0.25 0.50 0.25

7. Example 2 Solution
E(X) = 2.85.
x P(x) xP(x)
1 0.10 0.10
2 0.20 0.40
3 0.45 1.35
4 0.25 1.00
∑[xP(x)] = 2.85

8. VarianceVariance of a random variable X is
denoted by σ2. it can likewise be
written as Var(X).
The variance of a random variable is
the expected value of the square of
the difference between the assumed
value of random variable and the
mean.

9. Variance
Var(X) = ∑[(x – μ)2P(x)]
Or σ2 = ∑[(x – μ)2P(x)]
Where:
X = outcome
Μ = population mean
P(x) = probability of the outcome.

10. Variance
The larger the value of the variance,
the farther are the values of X from
the mean. The variance is tricky to
interpret since it uses the square of the
unit of measure of X. So, it is easier to
interpret the value of the standard
deviation because it uses the same unit
of measure of X.

11. Standard
DeviationThe standard deviation
of a discrete random
variable X is written as
σ. It is the square root of
the variance.

12. Example 3
Determine the variance and the standard
deviation of the following probability mass
function.
Calculate the expected value of X.
x 1 2 3 4 5 6
P(X) 0.15 0.25 0.30 0.15 0.10 0.05

13. Problems Involving
Mean and Variance
of Probability
Distribution
mhaykhel_3001

14. Example 1.
The officers of SJA Class 71 decided
to conduct a lottery for the benefit of
the less privileged students to their
alma matter. Two hundred tickets will
be sold. One ticket will win ₱5, 000
price and the other tickets will win
nothing. If you will buy one ticket,
what will be your expected gain.

15. Example 1.
x P(x) xP(x)
0 0.995 0
5, 000 0.005 25

16. Example 2.
The officers of faculty club of a public
high school are planning to sell 160
tickets to be raffled during the
Christmas party. One ticket will win
₱6, 000. the other tickets will win
nothing. If you are a faculty member
of the school and you will buy one
ticket, what will be the expected value
and variance of your gain?

17. Example 2.
x P(x) xP(x) x2P(x)
0 0.99375 0 0
3, 000 0.00625 18.75 56, 250

18. Example 3.
Jack tosses an unbiased
coin. He receives ₱50. if
a head appears and he
pays ₱30 if a tail appears.
Find the expected value
and variance of his gain.

19. Example 3.
x P(x) xP(x) x2P(x)
-30 0.5 -15 450
50 0.5 25 1250