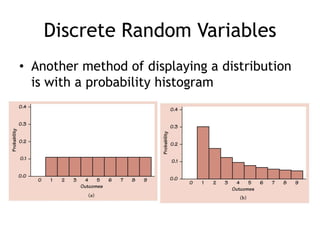
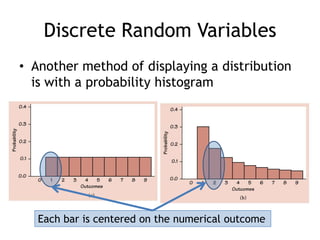
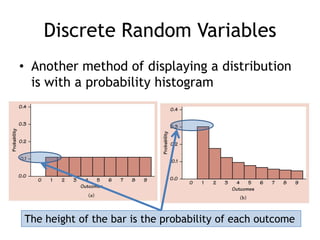
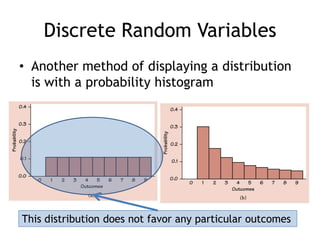
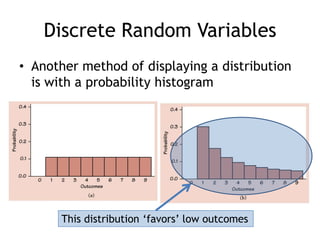
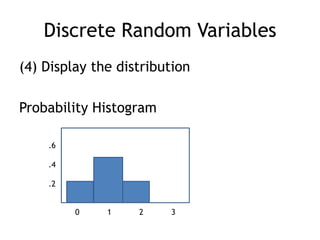
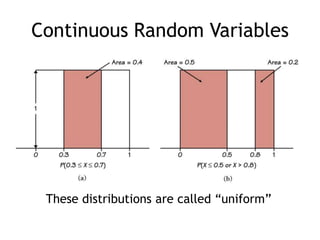
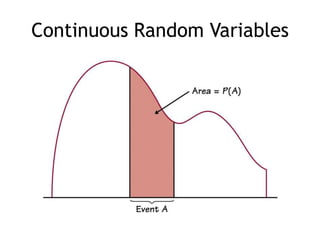
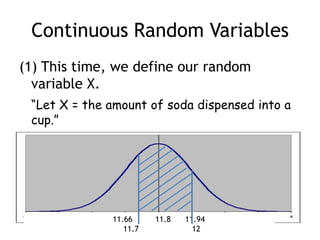
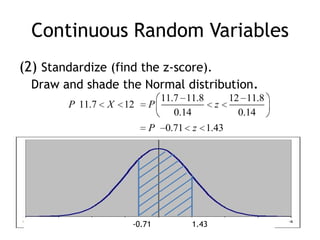
This document summarizes key concepts about random variables. It defines discrete and continuous random variables and explains how to represent their probability distributions. Discrete variables have countable outcomes and are represented by probability mass functions, while continuous variables have uncountable outcomes and are represented by density curves. The mean and variance are introduced as measures of central tendency and spread for random variables. Formulas are provided for calculating the mean and variance of discrete and continuous random variables. Transformations of random variables are also discussed.

1. Chapter 7 Random Variables

2. 7.1 Discrete and Continuous Random Variables

3. Random Variables A random variable is a variable whose value is a numerical outcome of a random phenomenon ex1 The sum of the pips on two dice ex2 The net gain or loss after a game of blackjack ex3 The amount of soda in a cup from a vending machine

4. Discrete Random Variable For a discrete random variable X, the number of outcomes is countable (finite) Ex3 (the soda from a vending machine) is not discrete. Why?

5. Discrete Random Variable Discrete random variables are often displayed using a “probability distribution” Value of X: x1 x2 x3 … xn Probability: p1 p2 p3… pn

6. Discrete Random Variable Discrete random variables are often displayed using a “probability distribution” Value of X: x1 x2 x3 … xn Probability: p1 p2 p3… pn P(X=x1)=p1 “Probability that X = x1 is p1”

7. Discrete Random Variable Discrete random variables are often displayed using a “probability distribution” Value of X: x1 x2 x3 … xn Probability: p1 p2 p3… pn Must add to ‘1’ p1 + p2 + … + pn = 1

8. Discrete Random Variable A probability distribution for a 6-sided die This isn’t a fair die! X 1 2 3 4 5 6 P(X) 1/3 1/6 1/6 1/6 1/12 1/12

9. Discrete Random Variables Another method of displaying a distribution is with a probability histogram

10. Discrete Random Variables Another method of displaying a distribution is with a probability histogram Each bar is centered on the numerical outcome

11. Discrete Random Variables Another method of displaying a distribution is with a probability histogram The height of the bar is the probability of each outcome

12. Discrete Random Variables Another method of displaying a distribution is with a probability histogram This distribution does not favor any particular outcomes

13. Discrete Random Variables Another method of displaying a distribution is with a probability histogram This distribution ‘favors’ low outcomes

14. Discrete Random Variables STEPS Define the random variable List all possible event Compute the probability of each event Display the distribution

15. Discrete Random Variables Let look at the probability distribution for the number of ‘heads’ produced by flipping two fair coins

16. Discrete Random Variables Define the random variable “Let X = the number of heads produced by flipping two fair coins”

17. Discrete Random Variables (2) List all possible outcomes Remember that each coin is independent Tip: be systematic when listing outcomes Let’s look at the outcomes that have ‘0 heads’ TT there’s only one of these

18. Discrete Random Variables How many outcomes have ‘1 heads’HTTHtwo outcomes!

19. Discrete Random Variables How many outcomes have ‘2 heads’HHonly one outcome There were 4 equally likely outcomes

20. Discrete Random Variables (3) Compute the probability of each event “# outcomes for event/# of outcomes P(X = 0) = ¼ P(X = 1) = 2/4 = ½ P(X = 2) = ¼

21. Discrete Random Variables (4) Display the distribution Probability Distribution

22. Discrete Random Variables (4) Display the distribution Probability Histogram .6 .4 .2 0 1 2 3

23. Continuous Random Variables Unlike the discrete random variable, a continuous random variable has an uncountable number of outcomes A continuous random variable X takes on all values in an interval of numbers

24. Continuous Random Variables The probability distribution for a continuous rand var is described/ displayed with a density curve. The probability of an event is the area under the density curve and above the values of X that make up the event The area under a density curve is ‘1’ A density curve lies above the x-axis at all points.

25. Continuous Random Variables These distributions are called “uniform”

26. Continuous Random Variables

27. Continuous Random Variables Curiously, since there is no area above any single value of x, P(X = x) = 0 for all values of x

28. Continuous Random Variables The Normal distribution is also a density curve! P( - < z < ) = 1 If a random variable can be transformed into the Normal distribution, we can use methods we learned earlier to compute probability!

29. Continuous Random Variables EXAMPLE A soda machine dispenses soda into a 12 oz paper cup. The amount of soda dispensed if Normal with  = 11.8 oz and  = 0.14 oz. What proportion of cups dispensed are between 11.7 and 12 ozs?

30. Continuous Random Variables Remember these: State problem in terms of ‘x,’ the observed variable. Draw and shade the distribution of ‘x.’ Standardize (find the z-score). Use proper notation!Draw and shade the Normal distribution. Find the area using Table A or your calculator.Remember that the area under curve is ‘1.’ Write up a conclusion in context of the problem.

31. Continuous Random Variables (1) This time, we define our random variable X. “Let X = the amount of soda dispensed into a cup.” 11.66 11.8 11.94 11.7 12

32. Continuous Random Variables (2)Standardize (find the z-score). Draw and shade the Normal distribution. -0.71 1.43

33. Continuous Random Variables (3) Find the area using Table A or your calculator.Remember that the area under curve is ‘1.’ P(-0.71<z<1.43) = 0.6848 (4) Write up a conclusion in context of the problem. “The proportion of cups whose volume of soda is between 11.7 and 12 ozs is 0.6848”

34. 7.2 Means and variances of random variables

35. Mean of a Random Variable Symbol is ‘mu’ (again) This mean is often called the “expected value” Ex The expected value does not have to be a possible value of X because it describes behavior over the long run

36. Mean of a Random Variable Discrete Random Variables:The mean is the sum of the products of the values and their probability X = x1p1 + x2p2 + x3p3 + … + xnpn X = xipi

37. Mean of a Random Variable Continuous Random Variables: We use techniques from chapter 2 to describe the relative location of the mean (depending on the shape of the density curve) Unless the curve is “well known” (i.e.Normal), we will not find the actual numerical value of the mean.

38. Variance of a Random Variable Discrete Random Variables X2 = (x1 - X)2·p1 + (x2 - X)2·p2 + (x3 - X)2·p3 + … + (xn - X)2·pn X2 = (xi - X)2·pi Yes, this formula is quite long and tiresome Calculator talk:If L1 = xi and L2 = pi, then X2 = sum(L1 - X)2·L2

39. Statistical Estimation Here’s the problem:We would like to know the mean height of American males. BUT, we cannot have a census. Solution:take a sample of American males and compute the mean height of the sample.

40. Statistical Estimation Suppose we took many samples. The histogram for the means of the samples will have it’s own distribution remember, this is the distribution of the means of the samples, and not the distribution of the heights of American males This distribution of the samples is called a “sampling distribution”

41. The Law of Large Numbers For any distribution, as the number of observations increases in the sample, the sample mean (Xbar) will approach the population mean . This is true for all distributions, not just Normal distributions.

42. The Law of Large Numbers Remember the following for random behavior: Behavior in the short run is unpredictable Behavior in the long run is regular and predictable This is the Law of Large Numbers This begs the question, how many observations is “the long run?”

43. Transformations for Means If a random variable undergoes a linear transformation to form a new random variable, Then the mean of the new random variable undergoes the same transformation. If: X2 = a + bX1 Then: X2 = a + b X1

44. Combining Two Means If two random variables are added/subtracted to for a new random variable, Then the mean of the new random variable is the two means added/subtracted IF: X = X1 ± X2 Then X = X1± X2

45. Transformations for Variance If a random variable undergoes a linear transformation, Then the variance of the new random variable is the product of the square of the multiplier and the old variance If: X2 = a + bX1 Then: (X2)2 = b2· (X1)2 Std Dev is the square root of variance

46. Combining Two Variances If two random variables are added/subtracted to for a new random variable, Then the variance of the new random variable is the sum of the squares of the old variances IF: X = X1 ± X2 Then (X)2 = (X1)2+ (X2)2 ALWAYS ADD VARIANCES Std Dev is the square root of variance

47. Normal Random Variables Any linear combination or transformation of Normal random variables is also Normal. IMPORTANT: you must state that a distribution is Normal before you can use techniques for Normal density curves. Especially true after a linear combination or transformation.

48. WILSON!!!! It’s doubtful that this is Normal behavior