This document provides an overview of random variables and various discrete probability distributions. It defines random variables and describes discrete and continuous random variables. It also covers the mean, variance, and standard deviation of discrete random variables. Various discrete probability distributions are introduced, including the discrete uniform distribution, Bernoulli distribution, and binomial distribution. Examples are provided to illustrate key concepts.

1. random variables
and Probability
Unit I

2. random variables
By: Kyla Sofiah Lachica
1.1-

3. Random Variable
Is a variable that can take on values
based on the outcomes of a random
experiment. A random variable is usually
denoted by an uppercase letter of the
alphabet and its posible values are denoted
with the corresponding lowercase letter. As
an example consider a tossing a cin at the
same time.

4. Random Variable
POSIBLE
OUTCOME
HHH HTH THH HHT HTT TTH THT TTT
Value of
X
3 2 2 2 1 1 1 0

5. 2 TYPES OF RANDOM VARIABLE

6. A discrete random variable is a
random variable that can take only whole
number values, outcomes that are
countable. This type of variable is
associated with experimets for which there
are a finite number of possible outcomes.

7. Example:
• Let X= number of students randomly selected to be
interviewed by a researcher. this is a discrete random
variable because its possible values are 0,1,2,3 and so
on.
• Let Y= number of left-handed teachers randomly
selected in a faculty room. this is a discrete random
variable because its posible values are 0,1,2,3 and so
on.

8. • Let Z= number of defective light bulbs
among the randomly selected light bulbs.
This is a discrete random variable
because the number of defective light
bulbs, which X can assume are 0,1,2,3
and so on.

9. A continous random variable is a
random variable that can take on non-
integral values as they take on values
contained in an interval. This random
variable is used for experiment with
infnitely may possible outcomes and its
commonly used for measurement such as
length, weight, and time.

10. A listing of all possible values of a
discrete random variable along with their
corresponding probabilities is called a
discrete probability distribution. The
discrete probability distribution can be
presented in tabular, graphical or in a
formula form.

11. Example:
• Let X= the lengths of randomly selected
shoes of senior students in centimeters.
The lengths of shoes of the students can
be between two given lenths. The values
can be obtained by using a measuring
device, a ruler. Hence, the random
variable X is a continous random
variable.

12. • Let Z= the hourly temperature last
sunday. Z is a continous random variable
because its values can be between any of
two given temperatures resulting from the
use of thermometer.

13. • The given spinner is divided into four
section. Let X be the score where the arrow
will stop (numbered as 1,2,3, and 4 in the
drawing below.)
• a.Find the probability that the arrow will
stop at 1,2,3, and 4.
• b. Construct the discrete probability
distribution of the random variable X.

14. • The probability that the arrow will at any
of 4 divisions is 1 out of 4 or 1/4. Hence,
the probability of landing on 1 is 1 out of
4 or 1/4. The probability of landing 2 is 1
out of 4 or 1/4. The probability of landing
on 4 is also 1 out of 4 or 1/4. these
probabilities is shown below.

15. • When two fair dice are thrown
simultaneously the following are the
possible outcoes.
• We define the random variable X as the
sum of tw ooutcomes in throwing the two
fair dice simultaneously. The possible
values are 2,3,4,5,6,7,8,9,10,11,12.
• The probabailities of each of the possible
values P(x)

16. –The discrete probability distribution in
tabular form is given below.
X 2 3 4 5 6 7 8 9 10 11 12
P(x) 1/36 1/18 1/12 1/9 5/36 1/6 5/36 1/9 1/12 1/18 1/36

17. SOLUTION:
=P(2)+P(3)+P(4)+P(5)+P(6)+P(7)+P(8)+
P(9)+P(10)+P(11)+P(12)
=1
Therefore the distribution is a discrete
probability distribution.

18. Mean, variance,
and Standard
deviation of a
discrete random
variables
By: Vanessa Rivadulla
Gerlyn Jean Evora
1.2-

19. Mean of a Discrete Random Variables
The mean of a discrete random
variables are also called the expected
value of X. It is the weighed average of
all the values that the random variable
x assumes value or outcomes in every
trials of an experiment with their
corresponding probabilities.

20. The expected value of X is the
average of the outcomes that is likely to
be obtained of the trials are repeated
over and over again. The expected
value of X is denoted by E(X).

21.  
 )]
(
2
)
(
2 x
P
x 

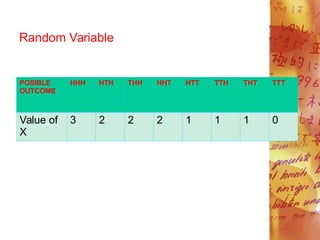
The mean or expected value of a
discrete random variable X is compted
using the following formula:
where: X= discrete random variable
x= outcome or the value of
random variable
P(x)= probability of the outcome x

22. Example
A researcher surveyed the households
is a small town. The random variable X
represents the number of college
graduates in the households. The
probability distribution of x is shown on
the next slide.

23. Find the expected value of X.
x 0 1 2
P(x) 0.25 0.50 0.25

24. Solution:
x P(x) xP(x)
0 0.25 0
1 0.50 0.50
2 0.25 0.50
=1.00
The expected value is 1. So the average number of
college graduates in the household of the smalltown is 1.

25. Example:
• A random variable X has this
probability distribution.
• Calculate the expected value.
x 1 2 3 4
P(x) 0.10 0.20 0.45 0.25

26. Solution:
x P(x) xP(x)
1 0.10 0.10
2 0.20 0.40
3 0.45 1.35
4 0.25 1.00
=2.85
So, E(X)=2.85.

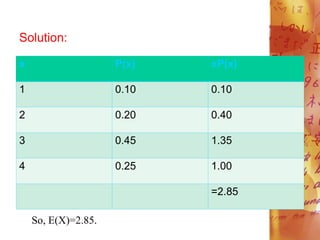
27. Variance and Standard Deviation of a Discrete
Random Variable
The variance of a random variable X is
denoted by o2. It can likewise be written as Var
(X). The variance of a random variable is the
expected value of the square of the difference
between the assumed value of random variable
and the mean. The variance of X is:
 
 )]
(
2
)
(
2 x
P
x 


28. The larger the value of variance ,
the farther are value of X from the
mean. The variance is tricky to interpret
since it uses the square of the unit of
measure of X. so, it easier to interpret
the value of the standard deviation
because it uses the same unit of
measure of X.

29. )
(
2
)
(
2 X
p
X
 
 

The standard deviaton of a discrete
random variable X is written as o. It is
the square root of the variance . The
standard deviaton computed as:

30. Example
Determine the variance and the
standard deviation of the following
probability mass function.
x P(x)
1 0.15
2 0.25
3 0.30
4 0.15
5 0.10
6 0.05

31. Solution:
a. Find the expected value
b. Subtract the expected value
from each outcome. Square each
difference
c. Multiply each difference ny
corresponding probability
d. Sum up all thefigures obtained
in Step 3.

32. x P(x) xP(x) x-u (x-u)2 (x-u)2P(x)
1 0.15 0.15 1-2.95=-1.95 3.8025 0.570375
2 0.25 0.50 2-2.95=-0.95 0.9025 0.225625
3 0.30 0.90 3-2.95=0.05 0.0025 0.000750
4 0.15 0.60 4-2.95=1.05 1.1025 0.165375
5 0.10 0.50 5-2.95=-2.05 4.2025 0.420250
6 0.05 0.30 6-2.95=3.05 9.3025 0.465125
=2.95 =1.8475

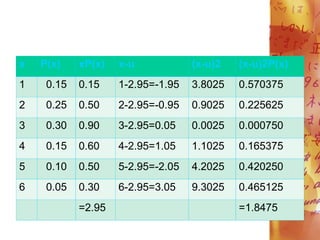
33. E(X)= 2. 95
=1.8475 or 1.85
Therefore, the standard deviation
is 1.85.
 
 )]
(
2
)
(
2 x
P
x 


34. PROBLEMS INVOLVING
MEAN AND VARIANCE OF
PROBABILITY
DISTRIBUTION
By: Joed Michael Beniegas
1.3-

35. THE LEARNER WILL BE ABLE TO:
- Interpret the mean and variance of a
discrete random variable
- Solve problem involving mean and variance
of probability distributions

36. The mean of a discrete random
variable can be thought of as
“anticipated” value. It is the average
that is expected to be the result when a
random experiment is continually
repeated. it is the sum of the possible
outcomes of the experiment multiplied
by their corresponding probabilities.

37. Just like in preview topic , the
mean wil be called expected value.

38. EXAMPLE 1:
The officers of SJA Class 71
decided to conduct a lottery for the
benefit of the less priveleged students
of their ama mater. Two hundred tickets
will be sold. One ticket will win P5,000
price and the other tickets will win
nothing. If you will buy one ticket, what
will be your expected gain?

39. SOLUTION:
x P(x) xP(x)
0 0.995 0
5000 0.005 25
=25
The expected gain is P25.00.
 )]
(
[ x
xP

40. EXAMPLE 2:
The officers of the facilty club of a
public high school are planning to sell
160 tickets to be raffled during the
Christmas party. One ticket will win
P3000. The other tickets will win
nothing. If you are a faculty member of
the school and you will buy one ticket,
what will be the expected value and
variance of your gain?

41. SOLUTION:
x P(x) xP(x) X2P(x)
0 0.99375 0 0
3000 0.00625 18.75 56,250
=18.75 =56,250
 )]
(
[ x
xP  )]
(
2
[ x
P
x

42. a. E(X)= [xP(x)]
=18.75
b. = [x2P(x) - ([xP(x)])2
= 56,250 - (18.75)2
= 56,250 - 351.5625
= 55,898.44

 
2


43. The expected value is P18.75.
The value of your gain is
55,898.44 and it indicates how spread
out the values of x are around the
mean. Given this large value, this
shows that the value are very far away
from each other.

44. EXAMPLE 3:
Jack tosses an unbiased coin. He
receives P50 if a head appears and he
pays P30 if a tail appears. Find the
expected value and variance of his
gain.

45. SOLUTION:
x P(x) xP(x) X2P(x)
-30 0.5 -15 450
50 0.5 25 1,250
=10 =1,700

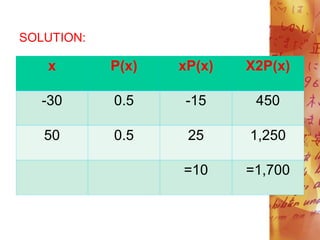
46. a. E(X)= [xP(x)]
=10
b. =[x2P(x) - ([xP(x)])2
= 1,700 - (10)2
= 1,700 - 100
= 1,600

47. The expected value is P10.
the variance of a gain is P1,600.

48. EXERCISES:
1.The officers of the Science Club
are planning to sell 125 tickets to be
raffled during the schools's foundation
day. One ticket will win P2,000 and the
other tickets will win nothing. If you will
buy one ticket, what will be your
expected gain?

49. 2. Laverny tosses unbiased coin.
He receives P100 of a head appears
and he pays P40 if a tail appears. Find
the expected value and the variance of
his gain.

50. other discrete
PROBABILITY
DISTRIBUTION
By: Angelo Genovana
1.4-

51. Discrete Uniform Distribution
A random variable has a discrete
uniform distribution where all the values
of the random variable are equally
likely, that is they have equal
probabilities.

52. If the random variable x assumes
the values x1, x2, x3... xn, that are
equally likely then it as a discrete
uniform distribution. The probability of
any outcome x, is 1/n.

53. Example:
When a far die is thrown, the
possible outcomes are 1, 2, 3, 4, 5, and
6. each time the die is thrown, it can roll
on any of these numbers. Since there
are six numbers, the probability of a
given score is 1/6. Therefore, we hav a
discrete uniform distributions.

54. •The probabilities are equal as shown
below.
P(1)= 1/6 P(2)= 1/6
P(3)= 1/6 P(4)= 1/6
P(5)= 1/6 P(6)= 1/6

55. The probabilty distributions of x is shown in
the table below, where the random variable x
represents the outcomes.
x 1 2 3 4 5 6
P(x) 1/6 1/6 1/6 1/6 1/6 1/6

56. Bernoulli Distribution
The Bernoulli distributions, named
after the Swiss mathematician Jacob
Bernoulli, is a probability distribution of
a random variable x which only two
possible outcomes. 1 and 0, that is
success and failure is q=1-p.

57. Binomial Probability Distribution
•A binomial experiment possesses the
following properties:
-the experiment conduct of a
repeated trials
-each trials is independent of the
previous trials

58. Thank You !
By: Group III