The document discusses different types of discrete probability distributions: - Uniform distribution where all outcomes are equally likely, like when rolling a fair die. - Bernoulli distribution which has only two possible outcomes (success/failure) with probabilities p and q=1-p. - Binomial distribution which describes experiments with a fixed number of trials, two possible outcomes per trial (success/failure), and where trials are independent with constant probability of success p.

1. –The discrete probability distribution in
tabular form is given below.
X 2 3 4 5 6 7 8 9 10 11 12
P(x) 1/36 1/18 1/12 1/9 5/36 1/6 5/36 1/9 1/12 1/18 1/36

2. SOLUTION:
=P(2)+P(3)+P(4)+P(5)+P(6)+P(7)+P(8)+
P(9)+P(10)+P(11)+P(12)
=1
Therefore the distribution is a discrete
probability distribution.

3. Mean, variance,
and Standard
deviation of a
discrete random
variables
By: Vanessa Rivadulla
Gerlyn Jean Evora
1.2-

4. Mean of a Discrete Random Variables
The mean of a discrete random
variables are also called the expected
value of X. It is the weighed average of
all the values that the random variable
x assumes value or outcomes in every
trials of an experiment with their
corresponding probabilities.

5. The expected value of X is the
average of the outcomes that is likely to
be obtained of the trials are repeated
over and over again. The expected
value of X is denoted by E(X).

6.  
 )]
(
2
)
(
2 x
P
x 

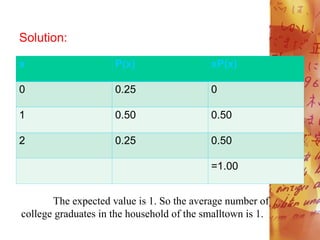
The mean or expected value of a
discrete random variable X is compted
using the following formula:
where: X= discrete random variable
x= outcome or the value of
random variable
P(x)= probability of the outcome x

7. Example
A researcher surveyed the households
is a small town. The random variable X
represents the number of college
graduates in the households. The
probability distribution of x is shown on
the next slide.

8. Find the expected value of X.
x 0 1 2
P(x) 0.25 0.50 0.25

9. Solution:
x P(x) xP(x)
0 0.25 0
1 0.50 0.50
2 0.25 0.50
=1.00
The expected value is 1. So the average number of
college graduates in the household of the smalltown is 1.

10. Example:
• A random variable X has this
probability distribution.
• Calculate the expected value.
x 1 2 3 4
P(x) 0.10 0.20 0.45 0.25

11. Solution:
x P(x) xP(x)
1 0.10 0.10
2 0.20 0.40
3 0.45 1.35
4 0.25 1.00
=2.85
So, E(X)=2.85.

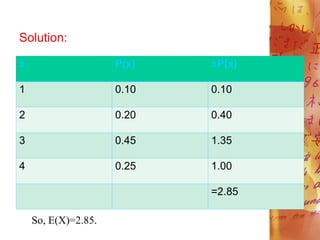
12. Variance and Standard Deviation of a Discrete
Random Variable
The variance of a random variable X is
denoted by o2. It can likewise be written as Var
(X). The variance of a random variable is the
expected value of the square of the difference
between the assumed value of random variable
and the mean. The variance of X is:
 
 )]
(
2
)
(
2 x
P
x 


13. The larger the value of variance ,
the farther are value of X from the
mean. The variance is tricky to interpret
since it uses the square of the unit of
measure of X. so, it easier to interpret
the value of the standard deviation
because it uses the same unit of
measure of X.

14. )
(
2
)
(
2 X
p
X
 
 

The standard deviaton of a discrete
random variable X is written as o. It is
the square root of the variance . The
standard deviaton computed as:

15. Example
Determine the variance and the
standard deviation of the following
probability mass function.
x P(x)
1 0.15
2 0.25
3 0.30
4 0.15
5 0.10
6 0.05

16. Solution:
a. Find the expected value
b. Subtract the expected value
from each outcome. Square each
difference
c. Multiply each difference ny
corresponding probability
d. Sum up all thefigures obtained
in Step 3.

17. x P(x) xP(x) x-u (x-u)2 (x-u)2P(x)
1 0.15 0.15 1-2.95=-1.95 3.8025 0.570375
2 0.25 0.50 2-2.95=-0.95 0.9025 0.225625
3 0.30 0.90 3-2.95=0.05 0.0025 0.000750
4 0.15 0.60 4-2.95=1.05 1.1025 0.165375
5 0.10 0.50 5-2.95=-2.05 4.2025 0.420250
6 0.05 0.30 6-2.95=3.05 9.3025 0.465125
=2.95 =1.8475

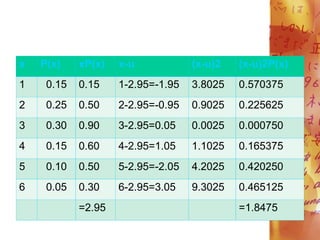
18. E(X)= 2. 95
=1.8475 or 1.85
Therefore, the standard deviation
is 1.85.
 
 )]
(
2
)
(
2 x
P
x 


19. PROBLEMS INVOLVING
MEAN AND VARIANCE OF
PROBABILITY
DISTRIBUTION
By: Joed Michael Beniegas
1.3-

20. THE LEARNER WILL BE ABLE TO:
- Interpret the mean and variance of a
discrete random variable
- Solve problem involving mean and variance
of probability distributions

21. The mean of a discrete random
variable can be thought of as
“anticipated” value. It is the average
that is expected to be the result when a
random experiment is continually
repeated. it is the sum of the possible
outcomes of the experiment multiplied
by their corresponding probabilities.

22. Just like in preview topic , the
mean wil be called expected value.

23. EXAMPLE 1:
The officers of SJA Class 71
decided to conduct a lottery for the
benefit of the less priveleged students
of their ama mater. Two hundred tickets
will be sold. One ticket will win P5,000
price and the other tickets will win
nothing. If you will buy one ticket, what
will be your expected gain?

24. SOLUTION:
x P(x) xP(x)
0 0.995 0
5000 0.005 25
=25
The expected gain is P25.00.
 )]
(
[ x
xP

25. EXAMPLE 2:
The officers of the facilty club of a
public high school are planning to sell
160 tickets to be raffled during the
Christmas party. One ticket will win
P3000. The other tickets will win
nothing. If you are a faculty member of
the school and you will buy one ticket,
what will be the expected value and
variance of your gain?

26. SOLUTION:
x P(x) xP(x) X2P(x)
0 0.99375 0 0
3000 0.00625 18.75 56,250
=18.75 =56,250
 )]
(
[ x
xP  )]
(
2
[ x
P
x

27. a. E(X)= [xP(x)]
=18.75
b. = [x2P(x) - ([xP(x)])2
= 56,250 - (18.75)2
= 56,250 - 351.5625
= 55,898.44

 
2


28. The expected value is P18.75.
The value of your gain is
55,898.44 and it indicates how spread
out the values of x are around the
mean. Given this large value, this
shows that the value are very far away
from each other.

29. EXAMPLE 3:
Jack tosses an unbiased coin. He
receives P50 if a head appears and he
pays P30 if a tail appears. Find the
expected value and variance of his
gain.

30. SOLUTION:
x P(x) xP(x) X2P(x)
-30 0.5 -15 450
50 0.5 25 1,250
=10 =1,700

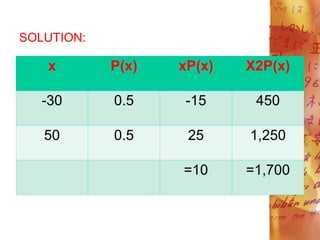
31. a. E(X)= [xP(x)]
=10
b. =[x2P(x) - ([xP(x)])2
= 1,700 - (10)2
= 1,700 - 100
= 1,600

32. The expected value is P10.
the variance of a gain is P1,600.

33. EXERCISES:
1.The officers of the Science Club
are planning to sell 125 tickets to be
raffled during the schools's foundation
day. One ticket will win P2,000 and the
other tickets will win nothing. If you will
buy one ticket, what will be your
expected gain?

34. 2. Laverny tosses unbiased coin.
He receives P100 of a head appears
and he pays P40 if a tail appears. Find
the expected value and the variance of
his gain.

35. other discrete
PROBABILITY
DISTRIBUTION
By: Angelo Genovana
1.4-

36. Discrete Uniform Distribution
A random variable has a discrete
uniform distribution where all the values
of the random variable are equally
likely, that is they have equal
probabilities.

37. If the random variable x assumes
the values x1, x2, x3... xn, that are
equally likely then it as a discrete
uniform distribution. The probability of
any outcome x, is 1/n.

38. Example:
When a far die is thrown, the
possible outcomes are 1, 2, 3, 4, 5, and
6. each time the die is thrown, it can roll
on any of these numbers. Since there
are six numbers, the probability of a
given score is 1/6. Therefore, we hav a
discrete uniform distributions.

39. •The probabilities are equal as shown
below.
P(1)= 1/6 P(2)= 1/6
P(3)= 1/6 P(4)= 1/6
P(5)= 1/6 P(6)= 1/6

40. The probabilty distributions of x is shown in
the table below, where the random variable x
represents the outcomes.
x 1 2 3 4 5 6
P(x) 1/6 1/6 1/6 1/6 1/6 1/6

41. Bernoulli Distribution
The Bernoulli distributions, named
after the Swiss mathematician Jacob
Bernoulli, is a probability distribution of
a random variable x which only two
possible outcomes. 1 and 0, that is
success and failure is q=1-p.

42. Binomial Probability Distribution
•A binomial experiment possesses the
following properties:
-the experiment conduct of a
repeated trials
-each trials is independent of the
previous trials

43. Thank You !
By: Group III