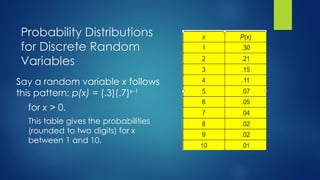
This document discusses random variables and probability distributions. It begins by introducing random variables and how they can be either discrete or continuous. Discrete random variables can take on countable values, while continuous can take on any value within an interval. Several examples of each are given, such as number of sales (discrete) and length (continuous). The document then discusses how to describe and find the probability distribution of a discrete random variable using a graph, table, or formula. It provides an example of a probability mass function and the expected values and variance of discrete random variables. Finally, it gives an example of calculating probabilities of winning or losing a bet in roulette.

1. RANDOM
VARIABLES AND
PROBABILITY
DISTIBUTIONS

2.  In our previous study of mathematics, we
encountered the concept of probability. How do
we use this concept in making decisions concerning
a population using sample?
 Decision- making is an important aspect in business,
education, insurance, and other real- life situations.
Many decisions are made by assigning probabilities
to all possible outcomes pertaining to the situation
and then evaluating the results.

3. LESSON 1:
EXPLORING RANDOM
VARIABLES

4. OBJECTIVES:
At the end of this lesson, you are expected to:
➢ Illustrate a random variable
➢ Classify random variables as discrete or
continuous; and
➢ Find the possible values of a random variable.

5. Two Types of Random Variables
 A random variable is a variable hat assumes
numerical values associated with the random
outcome of an experiment, where one (and only
one) numerical value is assigned to each sample
point.

6. Two Types of Random Variables
 A discrete random variable can assume a countable
number of values.
▪ Number of steps to the top of the Eiffel Tower*
 A continuous random variable can assume any value along
a given interval of a number line.
▪ The time a tourist stays at the top
once s/he gets there

7. Two Types of Random Variables
 Discrete random variables
 Number of sales
 Number of calls
 Shares of stock
 People in line
 Mistakes per page
 Continuous random variables
 Length
 Depth
 Volume
 Time
 Weight

8. Questions:
 1.) How do you describe a discrete random variable?
 2.) How do you describe a continuous random variable?
 3.) Give three examples of discrete random variable.
 4.) Give three examples of continuous random variable.

9. ACTIVITY:
TOSSING THREE COINS
 Suppose three coins are tossed. Let Y be the random variable
representing the number of tails that occur. Find the values of the
random variable Y. Complete the table below.
POSSIBLE OUTCOMES VALUE OF THE RANDOM VARIABLE Y
(Number of Tails)

10. EXERCISE:
 1.) Four coins are tossed. Let Z be the random variable representing the
number of heads that occur. Find the values of the random variable Z.
POSSIBLE OUTCOMES VALUE OF THE RANDOM VARIABLE Z

11. EXERCISE:
 Let T be a random variable giving the number of heads plus the
number of tails in three tosses of a coin. List the elements of the
sample space S for the three tosses of the coin and assign a value to
each sample point.
POSSIBLE OUTCOMES VALUE OF THE RANDOM VARIABLE T

12. QUIZ 1
Classify the following random variables as discrete or continuous.
1.) the number of defective computers produced by manufacturer
2.) the weight of newborns each year in a hospital
3.) the number of siblings in a family of region
4.) the amount of paint utilized in a building project
5.) the number of dropout in a school district for a period of 10 years
6.) the speed of car
7.) the number of female athletes
8.) the time needed to finish the test

13. 9.) the amount of sugar in a cup of coffee
10.) the number of people who are playing LOTTO each day
11.) the number of accidents per year at an intersection
12.) the number of voters favoring a candidate
13.) the number of bushels of apples per hectare this year
14.) the number of patient arrivals per hour at medical clinic
15.) the average amount of electricity consumed per household
per month

14. Probability Distributions for Discrete
Random Variables
 The probability distribution of a discrete random
variable is a graph, table or formula that specifies
the probability associated with each possible
outcome the random variable can assume.
p(x) ≥ 0 for all values of x
p(x) = 1

15. Probability Distributions
for Discrete Random
Variables
Say a random variable x follows
this pattern: p(x) = (.3)(.7)x-1
for x > 0.
This table gives the probabilities
(rounded to two digits) for x
between 1 and 10.

16. Expected Values of Discrete
Random Variables
 The mean, or expected value, of a
discrete random variable is
( ) ( ).
E x xp x
 = = 

17. Expected Values of Discrete
Random Variables
 The variance of a discrete random variable x is
 The standard deviation of a discrete random variable x is
2 2 2
[( ) ] ( ) ( ).
E x x p x
  
= − = −

2 2 2
[( ) ] ( ) ( ).
E x x p x
  
= − = −


18. Expected Values of Discrete
Random Variables
)
3
3
(
)
2
2
(
)
(












+


−
+


−
+


−
x
P
x
P
x
P

19. Expected Values of Discrete
Random Variables
 In a roulette wheel in a U.S. casino, a $1 bet on
“even” wins $1 if the ball falls on an even
number (same for “odd,” or “red,” or “black”).
 The odds of winning this bet are 47.37%
9986
.
0526
.
5263
.
1
$
4737
.
1
$
5263
.
)
1
$
(
4737
.
)
1
$
(
=
−
=

−

+
=
=
=


lose
P
win
P

20. That’s All
Thank you