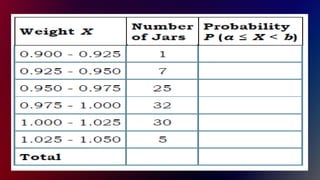
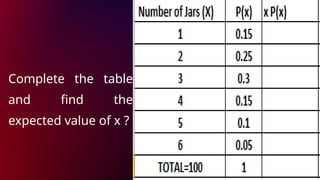
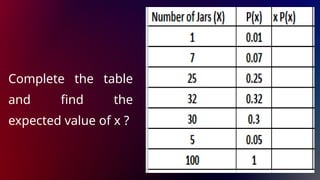
The document outlines the objectives and lessons related to random variables and probability distributions, focusing on distinguishing between discrete and continuous random variables. It includes examples, classification exercises, and definitions of key concepts such as sample space, probability distribution, expected value, and variance. Lessons also emphasize practical applications through problems and assignments.










































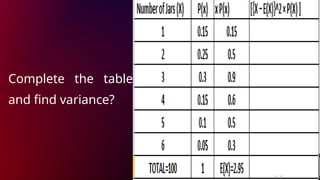
![• Let X represent a discrete random variable with probability
distribution P(X).
• The variance of X denoted by V(X) or σ^2 is defined as:
• V(X) = Σ[{X − E(X)}^2 × P(X) ]
VARIANCE OF A RANDON
VARIABLE](https://image.slidesharecdn.com/module1-241006041026-57cc3b09/85/MODULE-1-Random-Variables-and-Probability-Distributions-Quarter-3-Statistics-and-Probability-pptx-46-320.jpg)
![• Let X represent a discrete random variable with probability
distribution P(X).
• The variance of X denoted by V(X) or σ^2 is defined as:
• V(X) = Σ[{X − E(X)}^2 × P(X) ]
VARIANCE OF A RANDON
VARIABLE](https://image.slidesharecdn.com/module1-241006041026-57cc3b09/85/MODULE-1-Random-Variables-and-Probability-Distributions-Quarter-3-Statistics-and-Probability-pptx-47-320.jpg)