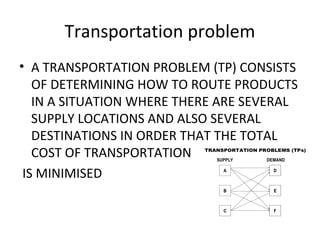
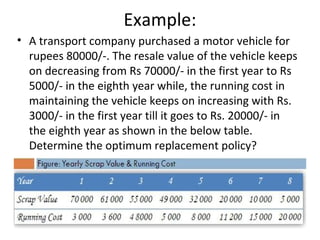
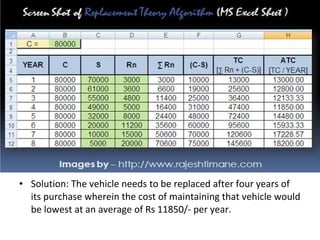
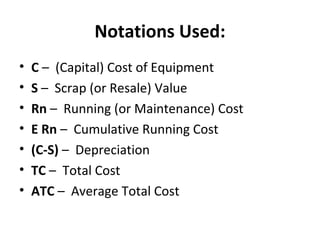
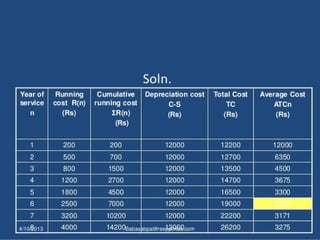
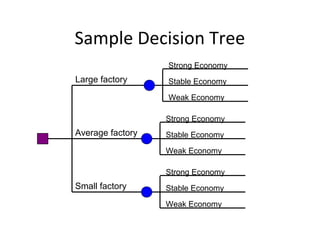
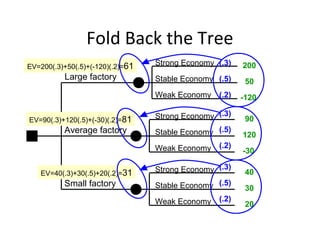
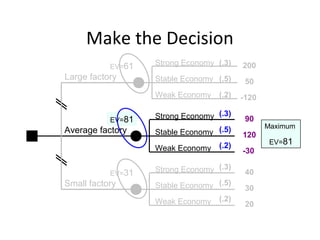
The document provides an overview of operations research techniques. It discusses:
- Operations research aims to improve decision-making through methods like simulation, optimization, and data analysis.
- Major applications include production scheduling, inventory control, transportation planning, and more.
- The techniques were developed in World War II and are now used widely in business for problems like resource allocation, forecasting, and process improvement.




















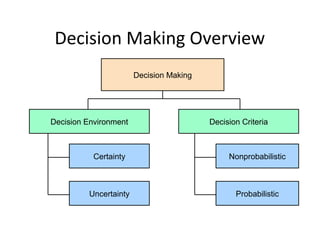
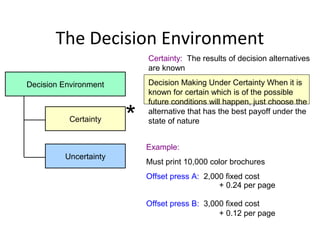
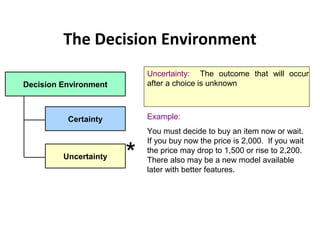




















![. IMPORTANT DEFINITIONS IN L.P.
Solution: A set of variables [X1,X2,...,Xn+m] is
called a solution to L.P. Problem if it satisfies its
constraints.
Feasible Solution: A set of variables
[X1,X2,...,Xn+m] is called a feasible solution to L.P.
Problem if it satisfies its constraints as well as non-
negativity restrictions
Optimal Feasible Solution: The basic feasible
solution that optimizes the objective function.
Unbounded Solution: If the value of the objective
function can be increased or decreased indefinitely,
the solution is called an unbounded solution](https://image.slidesharecdn.com/operationresearch-150115083732-conversion-gate01/85/Operation-research-complete-note-55-320.jpg)