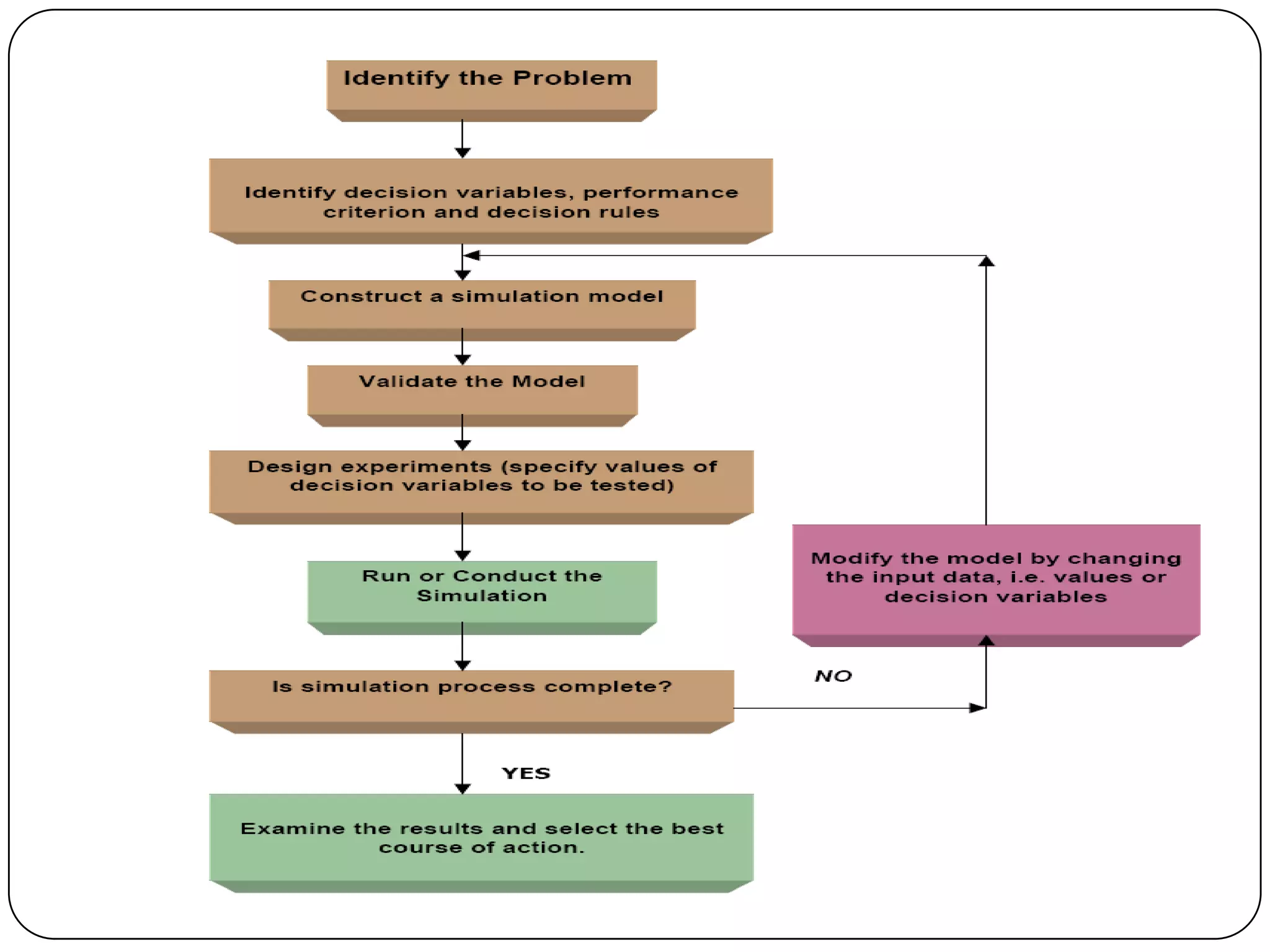
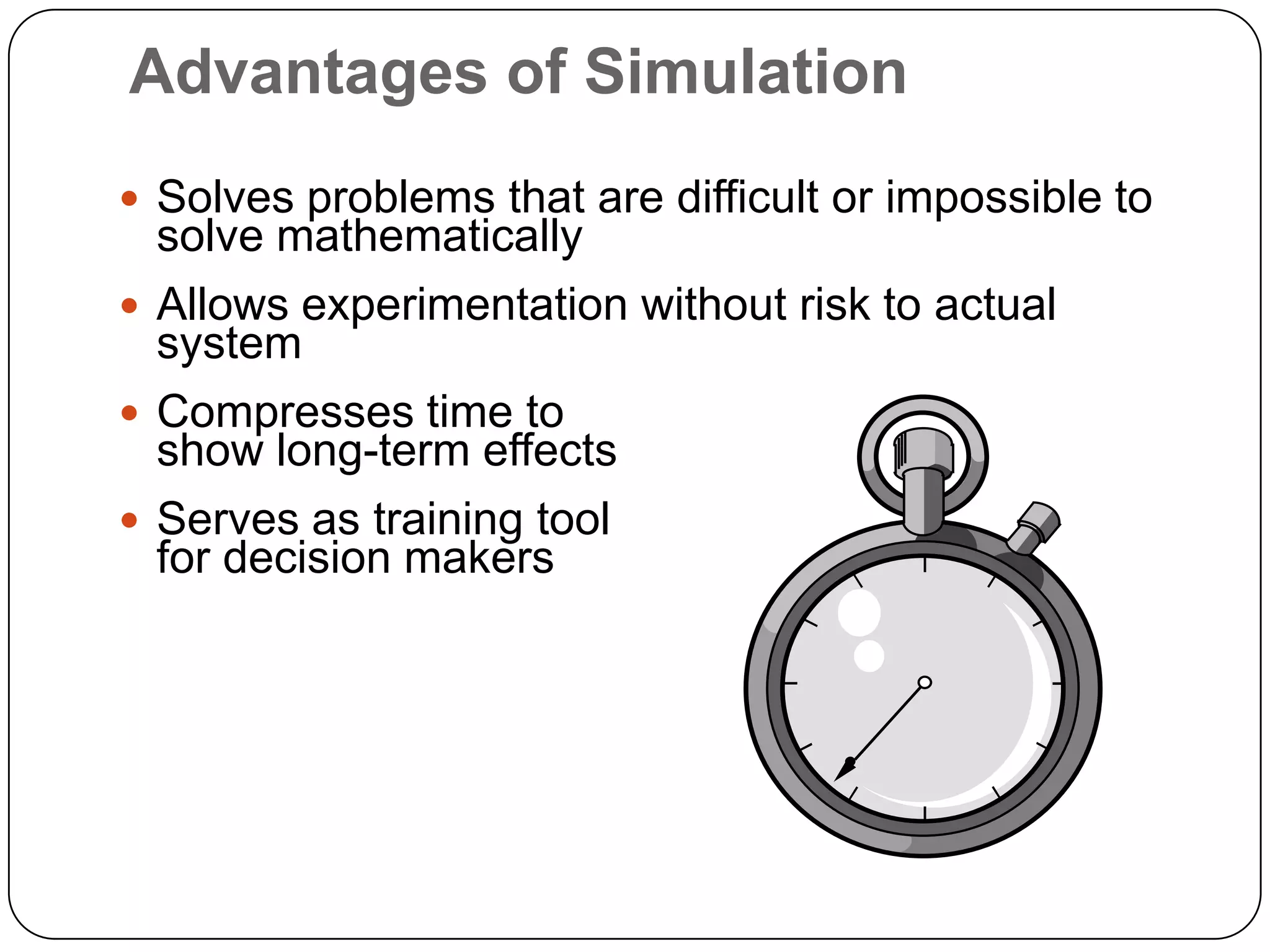
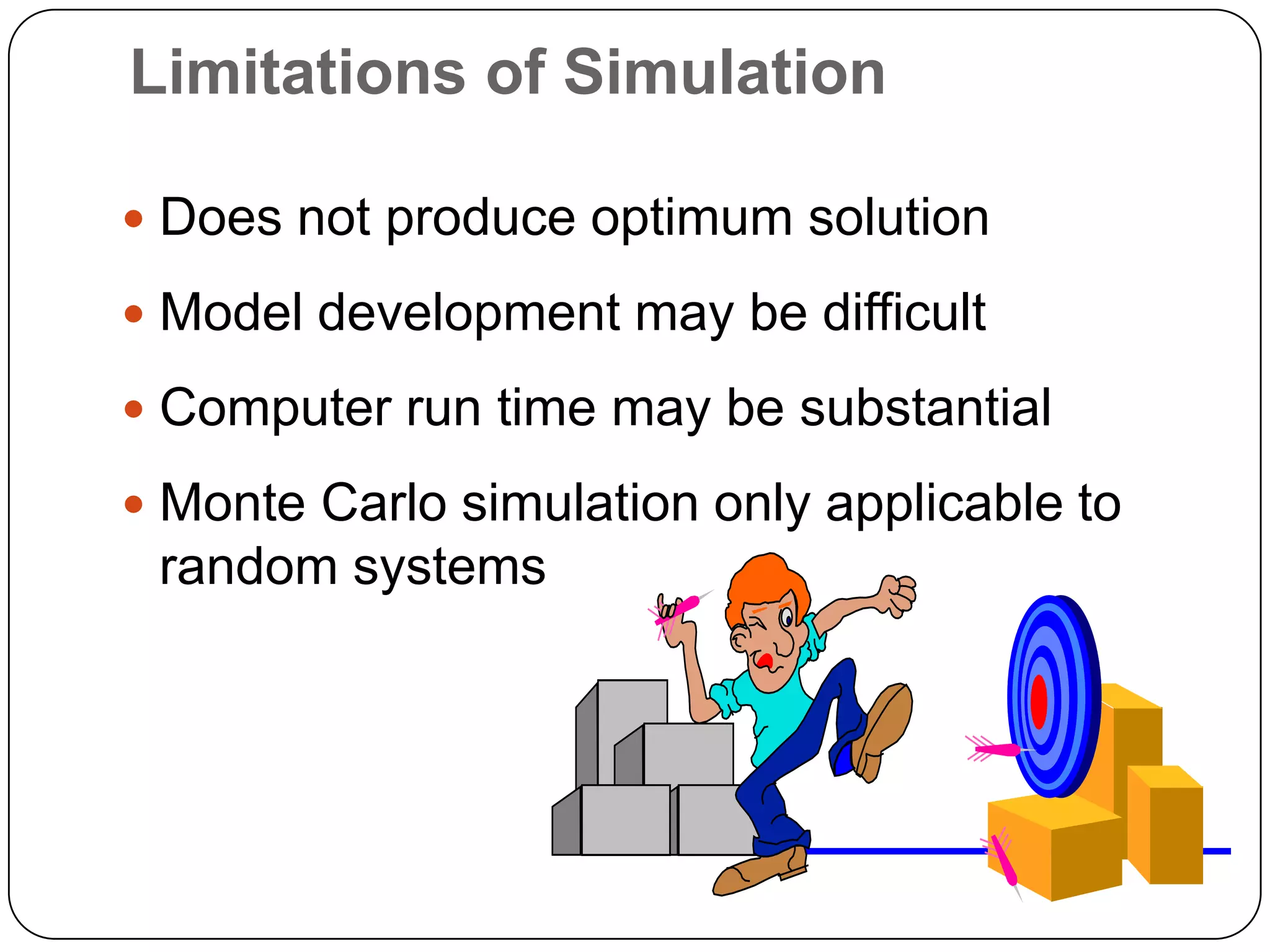
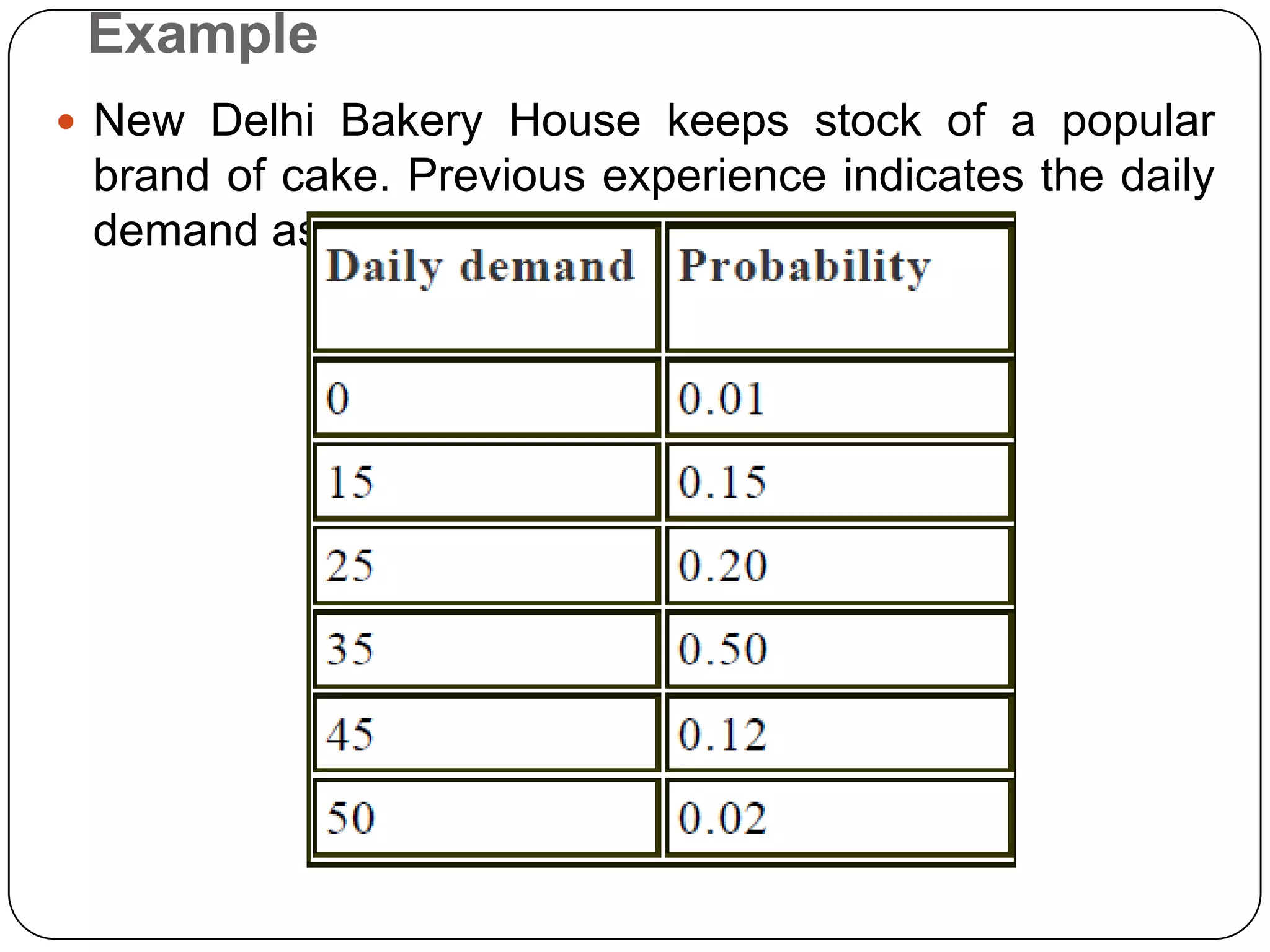
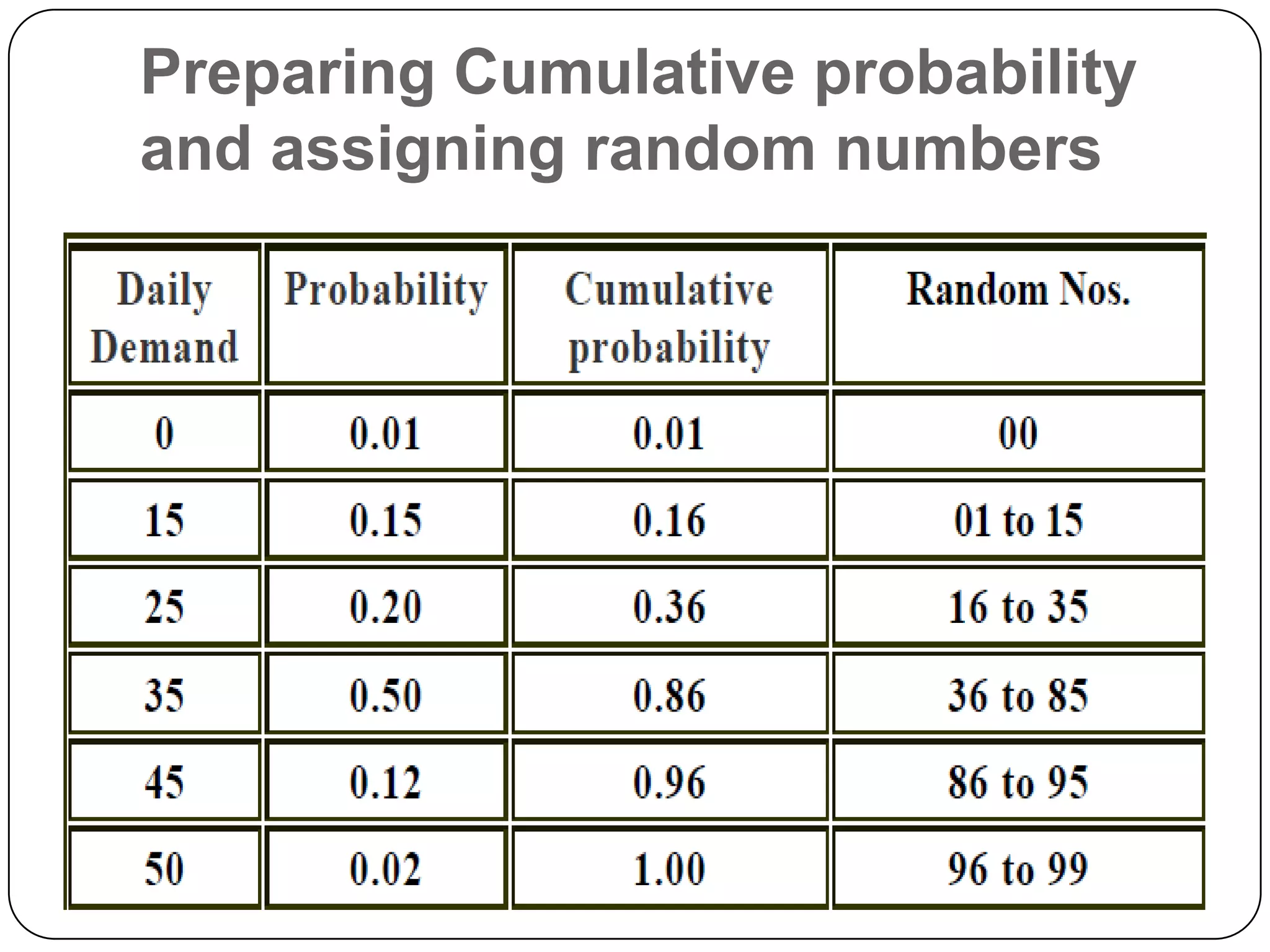
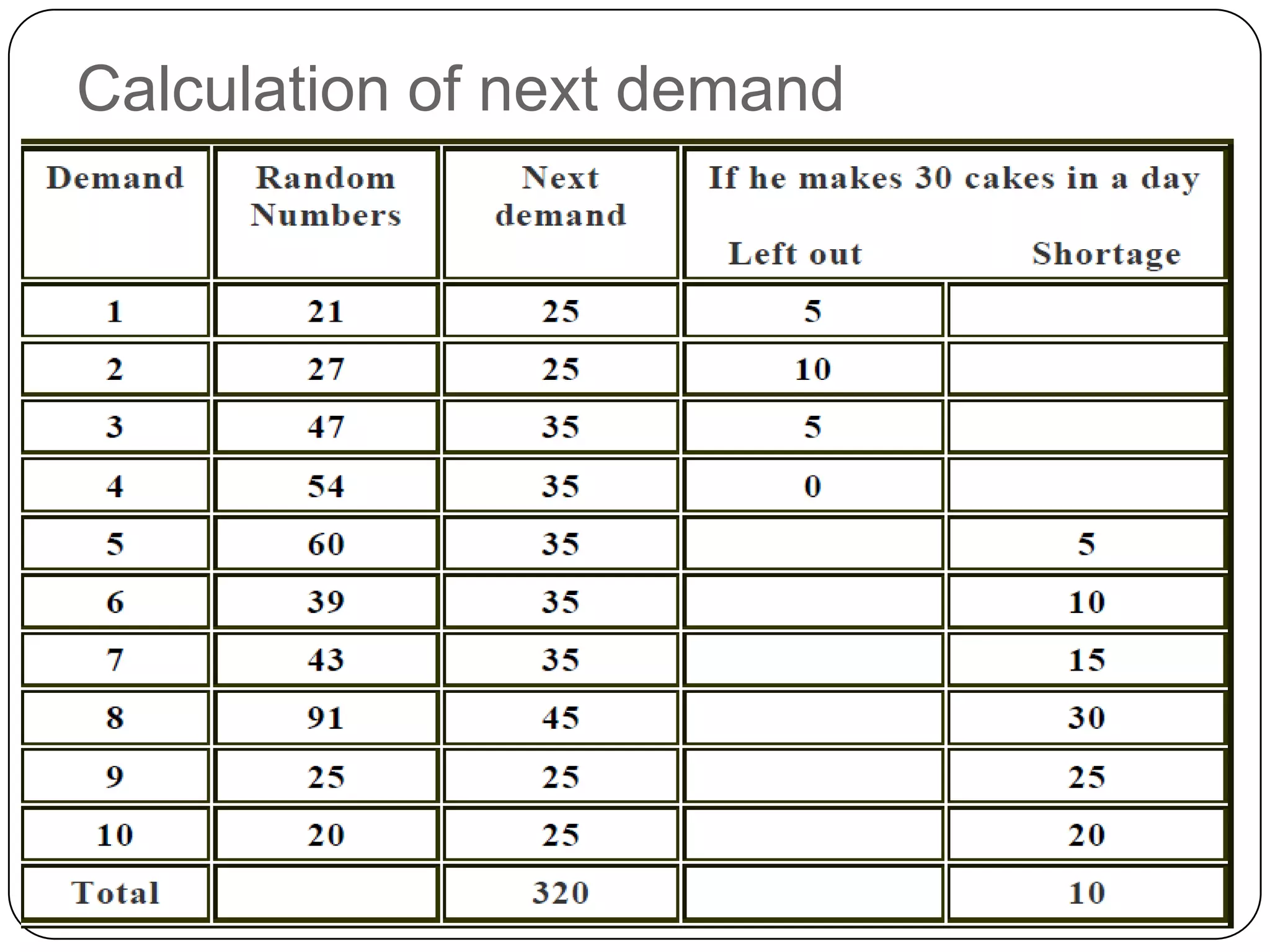
The document discusses simulation theory and the Monte Carlo method of simulation. It defines simulation as imitating reality and explains that simulation is used to understand complex systems when real experimentation is not possible or analytical solutions are unknown. It describes the Monte Carlo method as using probability distributions and random numbers to simulate random systems. The key steps are: (1) obtaining variable probabilities from data, (2) converting to cumulative probabilities, (3) generating random numbers, (4) mapping random numbers to probability intervals to determine outcomes, and (5) repeating simulations. An example demonstrates using cumulative probabilities and random numbers to simulate daily cake demand for a bakery.

1. Simulation Theory
ABU BASHAR

2. EVERYTHING IS
DIFFICULT
IF YOU CRY,
EVERYTHING IS
EASY
IF YOU TRY.

3. What is Simulation?
 Simulation means imitation of reality.
 The purpose of simulation in the business world
is to understand the behavior of a system.
 Before making many important decisions, we
simulate the result to insure that we are doing the
right thing.

4. When to use Simulation??
 First, when experimentation is not possible. Note that
if we can do a real experiment, the results would
obviously be better than simulation.
• Second condition for using simulation is when the
analytical solution procedure is not known. If analytical
formulas are known then we can find the actual
expected value of the results quickly by using the
formulas. In simulation we can hope to get the same
results after simulating thousands of times.

5.  Simulation is basically a data generation technique.
 Sometimes it is time consuming to conduct real
study to know about a situation or problem.
 An example is the simulation of the flow of
customers into and out of a bank, to help determine
service requirements. The use of simulation frees the
programmer and user from having to observe a bank
and keep track of exactly when each customer
arrives and leaves.
 Thus, simulation is used when actual
experimentation is not feasible.

6. Example
 We read and hear about Air force pilots being trained
under simulated conditions.
 Since it would be impossible to train a person when
an actual war is going on, all the conditions that
would prevail during a war are reconstructed and
enacted so that the trainee could develop the skills
and instincts that would be required of him during
combat conditions.
 Thus, war conditions are simulated to impart training.

7. Example Cont’d
 All automobile manufacturing companies have a test-
track on which the vehicles would be initially driven.
 The test-track would ideally have all the bends, slopes,
potholes etc., that can be found on the roadways on
which the vehicles would be subsequently driven.
 The test-track is therefore, a simulated version of the
actual conditions of the various roadways.
 Simulation, in general, means the creation of
conditions that prevail in reality, in order to draw certain
conclusions from the trials that are conducted in the
artificial conditions.
 A vehicle manufacturer, by driving the vehicle on the
test-track, is conducting a trial in artificial conditions in
order to draw conclusions regarding the road-

9. Types of simulation
 Deterministic and probabilistic Simulation
The deterministic simulation is used when process is very
complex or consists multiple stages with complicated (but
known) procedural interactions between them.
In probabilistic simulation, one or more of the independent
variables is probabilistic i.e. it follows a certain probability
distribution.
 Time dependent and Time independent simulation
In time independent simulation it is not important to known
exactly when the event is likely to occur. E.g. we know
demand of 3 units per day but don’t know when during the
day the item was demanded.
In time dependent it is important to know the precise time
when the event is likely to occur. In a queeing situation the
precise time of arrival of customer must be known (to know

10. Types of simulation Cont’d….
 Visual Interactive Simulation
It uses computer graphic displays to present the
consequences of change in the value of input
variation in the model. The decisions are implemented
interactively while the simulation is running. The
decision maker keep track of development of model
on a graphic interface and can alter the simulation as
it progress.
 Business Games
It involves several participants who need to play a role
in a game that simulates a realistic competitive
situation. Individual or teams compete to achieve their
goals in competition with the other individual or team.
 Corporate and Financial Simulation
It is used in corporate planning, especially the financial
aspects. The model integrate production, finance,
marketing, and possibly other functions, into one

11. Application of Simulation
Technique
 Simulation is widely used for the following
 Simulation of Inventory Problem
 Simulation of Queuing Problem
 Simulation of investment problem
 Simulation of Maintenance Problem
 Simulation of PERT Problem

12. Advantages of Simulation
 Solves problems that are difficult or impossible to
solve mathematically
 Allows experimentation without risk to actual
system
 Compresses time to
show long-term effects
 Serves as training tool
for decision makers

13. Limitations of Simulation
 Does not produce optimum solution
 Model development may be difficult
 Computer run time may be substantial
 Monte Carlo simulation only applicable to
random systems

14. Monte Carlo Method of
Simulation
 The principle behind this method of simulation is
representative of the given system under analysis
by a system described by some known probability
distribution and then drawing random samples for
probability distribution by means of random number.
 In case it is not possible to describe a system in
terms of standard probability distribution such as
normal, Poisson, exponential, etc., an empirical
probability distribution can be constructed.

15.  It can be usefully applied in cases where the system
to be simulated has a large number of elements that
exhibit chance (probability) in their behaviour.
 Simulation is normally undertaken only with the help
of a very high-speed data processing machine such
as computer.
 The user of simulation technique must always bear
in mind that the actual frequency or probability would
approximate the theoretical value of probability only
when the number of trials are very large i.e. when
the simulation is repeated a large no. of times.
 This can easily be achieved with the help of a
computer by generating random numbers.

16. steps involved in Monte-Carlo simulation
 Step I.
 Obtain the frequency or probability of all the
important variables from the historical sources.
 Step II.
 Convert the respective probabilities of the various
variables into cumulative probabilities.
 Step III.
 Generate random numbers for each such variable.
 Step IV.
 Based on the cumulative probability distribution table
obtained in Step II, obtain the interval (i.e.; the
range) of the assigned random numbers.
 Step V.
 Simulate a series of experiments or trails.

17. Example
 New Delhi Bakery House keeps stock of a popular
brand of cake. Previous experience indicates the daily
demand as given below

19. Preparing Cumulative probability
and assigning random numbers

20. Calculation of next demand

21.  Next demand is calculated on the basis of
cumulative probability (e.g., random number 21 lies
in the third item of cumulative probability, i.e., 0.36.
Therefore, the next demand is 25. )
 Similarly, we can calculate the next demand for
others.
 Total demand = 320
 Average demand = Total demand / no. of days
 The daily average demand for the cakes = 320 / 10 =
32 cakes.

22. THANK YOU
VERY MUCH