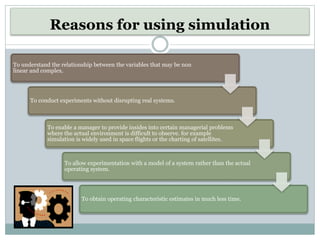
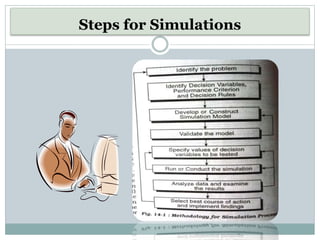
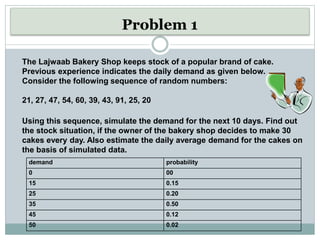
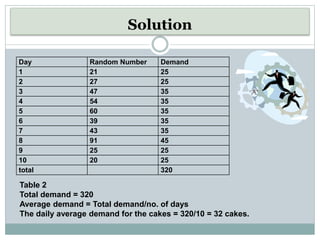
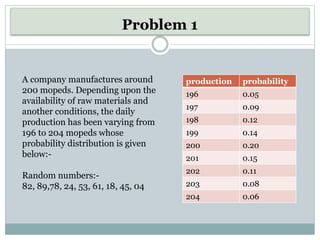
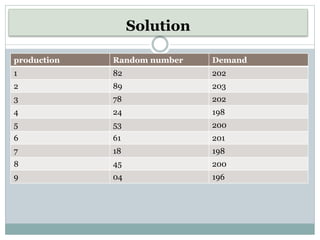
This document discusses simulation as a technique used in operations research to analyze the behavior of systems. It provides examples of how simulation works by initializing a system, generating inputs, observing outputs, and collecting statistics. Some key uses of simulation mentioned include testing policy decisions, conducting experiments without disrupting real systems, and obtaining operating characteristics estimates faster than working with actual systems. The document also outlines some advantages and limitations of the simulation approach. It includes two examples demonstrating how to simulate daily demand for a bakery and daily production for a moped manufacturer using random numbers.

1. SIMULATION
OPERATION RESEARCH
Presented by:
Komal Hambir
Nikita Jain
Bansri Shah
Ruchira Mohite

2. Simulation
Simulation is based on the random numbers and
probabilities, it provides the decision maker with useful
information like how likely each outcome can be expected.
This is a versatile tool which deals itself to the solution of
a large variety of O.R problems which are otherwise
difficult to solve.
It is a technique for carrying out experiments for
analyzing the behavior and evaluating the performance of
a proposed system under assumed condition of reality

3. Simulation
Simulation typically involves
• Initialization of the system to some specified
state.
• Generation of the inputs to the system.
• Operation of the system under the particular
state input configuration according to the
rules laid down by the procedural model.
• Observation and collection of statistics on the
performance of the system.

4. Reasons for using simulation
To understand the relationship between the variables that may be non
linear and complex.
To conduct experiments without disrupting real systems.
To enable a manager to provide insides into certain managerial problems
where the actual environment is difficult to observe. for example
simulation is widely used in space flights or the charting of satellites.
To allow experimentation with a model of a system rather than the actual
operating system.
To obtain operating characteristic estimates in much less time.

5. Applications
 Testing the impact of various policy decisions
through corporate planning models.
 Financial studies involving risky investments.
 Determining ambulance and fire fighting- fire
fighting equipments location and dispatching.
 Design of distribution system parking lots and
communication systems.
 Testing a series of inventory order policies to find the
least cost order point.

6. Steps for Simulations

7. Advantages
 Flexible and straightforward technique.
 To analyze large and complex real world systems.
 Used in solving problems where all values of the
variable are not known or are partly known.
 It does not interfere with real world system as
experiments are done with models and not on the
system itself.
 Easier to apply.

8. Limitations
Does not produce optimal results.
Very expensive as it takes years to develop a useable
corporate planning model.
Long and complicated process.
Each simulation process is unique and its solution and
interferences are not usually transferable to other
problems

9. Problem 1
demand probability
0 00
15 0.15
25 0.20
35 0.50
45 0.12
50 0.02
The Lajwaab Bakery Shop keeps stock of a popular brand of cake.
Previous experience indicates the daily demand as given below.
Consider the following sequence of random numbers:
21, 27, 47, 54, 60, 39, 43, 91, 25, 20
Using this sequence, simulate the demand for the next 10 days. Find out
the stock situation, if the owner of the bakery shop decides to make 30
cakes every day. Also estimate the daily average demand for the cakes on
the basis of simulated data.

10. Solution
Daily Demand Probability Cumulative
Probability
Random
Numbers
intervals
0 0.01 0.01 0
15 0.15 0.16 1-15
25 0.20 0.36 16-35
35 0.50 0.86 36-85
45 0.12 0.98 86-97
50 0.02 1.00 98-99
-Using the daily demand distribution, we obtain a probability distribution
as shown in the following table.
At the start of simulation, the first random number 21 generates a
demand of 25 cakes as shown in table 2. The demand is determined from
the cumulative probability values in table 1. At the end of first day, the
closing quantity is 5 (30-25) cakes.
Similarly, we can calculate the next demand for others.

11. Solution
Day Random Number Demand
1 21 25
2 27 25
3 47 35
4 54 35
5 60 35
6 39 35
7 43 35
8 91 45
9 25 25
10 20 25
total 320
Table 2
Total demand = 320
Average demand = Total demand/no. of days
The daily average demand for the cakes = 320/10 = 32 cakes.

12. A company manufactures around
200 mopeds. Depending upon the
availability of raw materials and
another conditions, the daily
production has been varying from
196 to 204 mopeds whose
probability distribution is given
below:-
Random numbers:-
82, 89,78, 24, 53, 61, 18, 45, 04
production probability
196 0.05
197 0.09
198 0.12
199 0.14
200 0.20
201 0.15
202 0.11
203 0.08
204 0.06
Problem 1

13. production probability Cumulative
probability
Random
number
intervals
196 0.05 0.05 00-4
197 0.09 0.14 5-13
198 0.12 0.26 13-25
199 0.14 0.40 26-3
200 0.20 0.60 40-59
201 0.15 0.75 60-74
202 0.11 0.86 75-85
203 0.08 0.94 86-93
204 0.06 1 94-100
Solution

14. production Random number Demand
1 82 202
2 89 203
3 78 202
4 24 198
5 53 200
6 61 201
7 18 198
8 45 200
9 04 196
Solution

15. Total demand = 1800
Average demand = total demand/no of days
1800/9
200 mepods/day
Solution