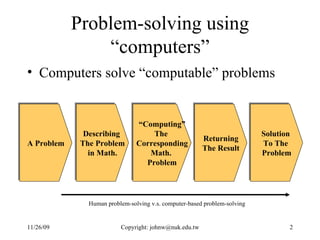
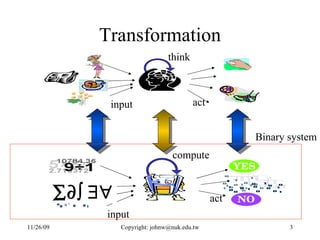
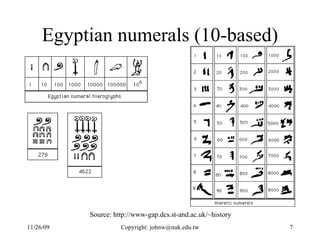
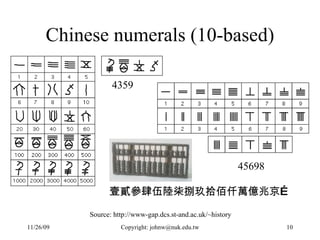
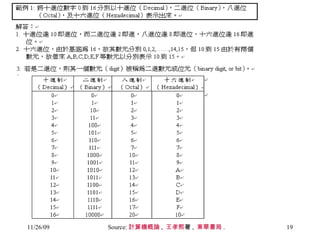
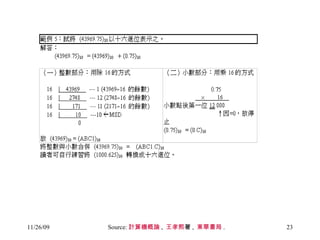
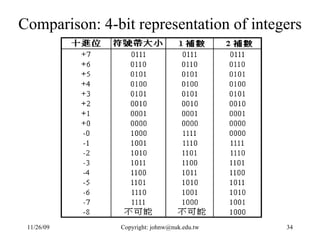
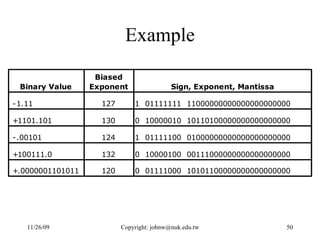
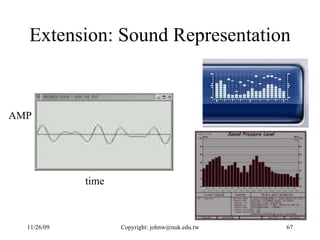
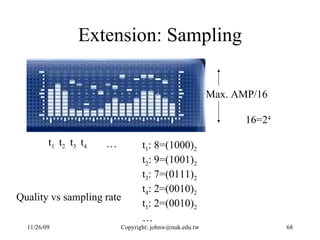
The document discusses number systems and data representation in computers. It explains that computers use the binary number system to represent numeric and alphanumeric data. Binary representations allow computers to distinguish different states using digits of 0 and 1. 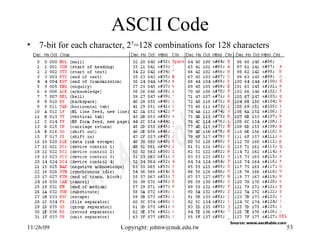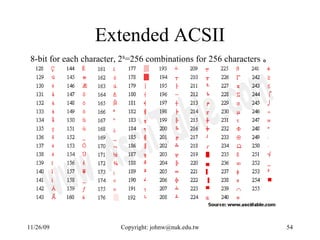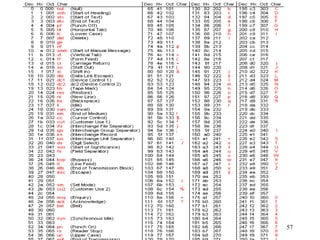The key points are: - Computers use the binary system to represent data as strings of bits (0s and 1s) that can be processed electronically - Numeric data such as integers are represented using binary formats like binary, sign-magnitude, 1's complement, and 2's complement - Text and character data are represented using coding schemes like ASCII which assign a unique binary code to each character - Floating point representation is used to store real numbers in a binary format using a sign bit,

1. Unit 4: The Number Systems and Data Representation

2. Problem-solving using “computers” Computers solve “computable” problems A Problem Describing The Problem in Math. “ Computing” The Corresponding Math. Problem Returning The Result Solution To The Problem Human problem-solving v.s. computer-based problem-solving

3. Transformation input think act input compute act   Binary system

4. The Number System A number system is to enumerate the “states” of something For example, money, days, month, year, minutes, hours, … In human’s world, we have very good tools   …which counts 10 states

5. The Needs of Number Systems However, there are some states are not Decimal. For example, Days and weeks Minutes and hours Months and year We need convenient representations for different “nature states”

7. Egyptian numerals (10-based) Source: http://www-gap.dcs.st-and.ac.uk/~history

8. Babylonians numerals (60-based) Source: http://www-gap.dcs.st-and.ac.uk/~history

9. 1*60 3 + 57*60 2 + 46*60 + 40*60 0 = 424000 Source: http://www-gap.dcs.st-and.ac.uk/~history

10. Chinese numerals (10-based) 4359 45698 Source: http://www-gap.dcs.st-and.ac.uk/~history 壹貳參肆伍陸柒捌玖拾佰仟萬億兆京…

11. The Number Systems A number system specifies how/what “numbers” represent and operate. A K-based number system uses N different symbols to represent N different entities or “states” Each symbol is a “digit” Multiple digits are used for describing M>N states

12. K-based Number System 2-based: ON/OFF; Yes/No; T/F; 1/0; etc. 3-based: A/B/C; True/False/Unknown; 0/1/2; etc. … 7-based: Mon/Tue/Wes/Thu/Fri/Sat/Sun; 0/1/2/3/4/5/6; etc. 8-based: ; 0/1/2/3/4/5/6/7

13. K-based Number System 10-based:  /  /  /  /  /  /  /  /  /  ; 0/1/2/3/4/5/6/7/8/9; etc. 16-based:  /  /  /  /  /  /  /  /  /  /  /  ; 0/1/2/3/4/5/6/7/8/9/A/B/C/D/E/F; etc. State-1 State-2 State-3 State-4 State-5 State-6 State-7 State-8 State-9 State-10 State-11 State-12 State-13 State-14 State-15 State-16

14. K-based Number System In the 16-based number system: 0/1/2/3/4/5/6/7/8/9/A/B/C/D/E/F; etc. Why not “ 1 0 ” 2 digits

15. More States In a 6-based number system  : state 1 (empty state) (0)  : state 2 (1 st )  : state 3 (2 nd )  : state 4 (3 rd )  : state 5 (4 th )  : state 6 (5 th )  : state 7 (6 th )  : state 8 (7 th )  : state 9 (8 th )  : state 10 (9 th )  : state 11 (10 th )  : state 12 (13 th ) …

16. More States In a 6-based number system 0: state 1 (empty state) (0) 1: state 2 (1 st ) 2: state 3 (2 nd ) 3: state 4 (3 rd ) 4: state 5 (4 th ) 5: state 6 (5 th ) 10: state 7 (6 th ) 11: state 8 (7 th ) 12: state 9 (8 th ) 13: state 10 (9 th ) 14: state 11 (10 th ) 15: state 12 (13 th ) 20: state 13 (14 th ) …

17. The Number of Cases Generally, in a K-based number system, 1 digit describes K 1 cases 2 digits describes K 2 cases 3 digits describes K 3 cases N digits describes K N cases For example, 2 3-based (0,1,2) digits: 00, 01, 02, 10, 11, 12, 20, 21, 22 (3 2 =9 cases) 3 10-based (0,1,2,..,9) digits: 000, 001, 002, 003, 004, 005, 006,007, 008, 009, 010, 011,…,998, 999 (10 3 =1000 cases)

18. K-based vs The Decimal system (10-based) In general, any K-based number N can be expressed as Usually, N k is denoted as (A p-1 A p-2 ….A 1 A 0 . A -1 A -2 ….A -q ) k A p-1 :Most Significant Digit, MSD A -q :Least Significant Digit, LSD

19. Source: 計算機概論 , 王孝熙 著 , 東華書局 .

20. Using octal and hex numbers Computers use binary, but the numbers are too long and confusing for people Translation between binary and octal or hex is easy One octal digit equals three binary digits 101101011100101000001011 5 5 3 4 5 0 1 3 One hexadecimal digit equals four binary digits 101101011100101000001011 B 5 C A 0 B

21. Source: 計算機概論 , 王孝熙 著 , 東華書局 .

22. Source: 計算機概論 , 王孝熙 著 , 東華書局 .

23. Source: 計算機概論 , 王孝熙 著 , 東華書局 .

24. Source: 計算機概論 , 王孝熙 著 , 東華書局 .

25. Source: 計算機概論 , 王孝熙 著 , 東華書局 .

26. Source: 計算機概論 , 王孝熙 著 , 東華書局 .

27. The binary number system In modem computers, the binary number system is easier to be implemented. Currently, they are implemented in silicon chips (VLSI) Circuits for computation 01111 00011 10010 15 3 + 10 + 2 18

28. The binary number system The binary (base 2 or 2-based) number system uses two “binary digits, ” (abbreviation: bits) -- 0 and 1 A bit is a single two-valued quantity: yes or no, true or false, on or off, high or low, good or bad One bit can distinguish between two cases: T, F (True/False; Yes/No) Two bits can distinguish between four cases: TT, TF, FT, FF Three bits can distinguish between eight cases: TTT, TTF, TFT, TFF, FTT, FTF, FFT, FFF In general, n bits can distinguish between 2 n cases A byte is 8 bits, therefore 2 8 = 256 cases

29. Data Processing in Computers with the Binary System Data processing in binary computers Numeric data: +2, -5.5, 50000.235698, etc. Alphanumeric data: characters, name, address, telephone number, etc. Two main tasks: All data are converted into proper binary formats (bits) Rules for counting and computing these bits

30. Part I: Numeric Data Numeric data: integers, real positive, negative Representation of numeric data Sign-magnitude 1’s Complement 2’s Complement Negative/Positive in a n-bit integer I I=(A n-1 A n-2 ….A 1 A 0 ) 2 A n-1 = “0”, I is positive A n-1 =“1”, I is negative

31. Sign-Magnitude An n-bit integer I= Min: 00000…0 (n-1 0’s)=0 Max: 11111…1 (n-1 1’s)=2 n-1 -1 +0= (0000) 2 vs –0=(1000) 2 +3= (0011) 2 vs –3=(1011) 2 Disadvantages 2 different 0’s (+0/-0 ） Not easy to be implemented in simple circuits (usually adder)

32. 1’s Complement An n-bit integer I= For positive integers: the same as that in sign-magnitude For negative integers: complement their positive representations For example: 4-bit integers: +3=(0011) 2 ， -3=(1100) 2 +0=(0000) 2 ， -0=(1111) 2 Disadvantages 2 different 0’s (+0/-0 ） Easy to be implemented in simple circuits (usually adder) but not as efficient as 2’s complement

33. 2’s Complement An n-bit integer I= For positive integers: the same as that in sign-magnitude For negative integers: find their 1’s complement + 1 For example: 4-bit integers: +3 = (0011) 2 ， -3 = (1100) 2 +1 = (1101) 2 +0 = (0000) 2 ， -0 = (1111) 2 + 1 = (0000) 2 There is only one “0”

34. Comparison: 4-bit representation of integers

35. Range of integers Suppose that we use a byte (8-bit) to represent an integer (00000000) 2 (00000000) 2 (10000000) 2 =-128 (01111111) 2 =+127 2‘s complement (11111111) 2 (00000000) 2 (10000000) 2 =-127 (01111111) 2 =+127 1‘s Complement (10000000) 2 (00000000) 2 (11111111) 2 =-127 (01111111) 2 =+127 Sign-Magnitude -0 +0 Max. (-) Max. (+) -(2 n-1 )~0 0~2 n-1 -1 2‘s complement -(2 n-1 -1)~0 0~2 n-1 -1 1‘s Complement -(2 n-1 -1)~0 0~2 n-1 -1 Sign-Magnitude Negative numbers Positive numbers

36. Note Representation level Implementation level

37. Other Binary Codes for Decimal Numbers BCD code 2421 code Excess-3 code 84-2-1 code 4-bit for a number (0~9)

38. 8421 BCD Code In the 8421 Binary Coded Decimal (BCD) representation each decimal digit is converted to its 4-bit pure binary equivalent. Each decimal number maps to four bits and is weighted by its bit-position (each bit represents a number, 1, 2, 4, 8) BCD code is also called as 8421 code

39. 4221 BCD Code In 4221 BCD code, each bit is weighted by 4, 2, 2 and 1 respectively. Unlike BCD coding there are no invalid representations. advantages

40. Excess-3 Code Add 3 for each binary number Examples Excess-3 code of “2 10 ” = (0010) 2 +(0011) 2 =(0101) 2 Excess-3 code of “5 10 ” = (0101) 2 +(0011) 2 =(1000) 2 Advantages

41. 84-2-1 Code 4-bit for each number (0~9) weighted (left to right) as 8, 4, -2, and -1 。 Example 84-2-1 code of “3” = 0101 (0+4+0+(-1)=3) 84-2-1 code of “5” =1011 (8+0+(-2)+(-1)=5)

42. Self-complementing code Source: 計算機概論 , 王孝熙 著 , 東華書局 .

43. Gray Codes In pure binary coding or 8421 BCD, counting from 7 (0111) to 8 (1000) requires 4 bits to be changed simultaneously. If this does not happen then various numbers could be momentarily generated during the transition so creating spurious numbers which could be read. In gray coding, only one bit changes between subsequent numbers. Generating gray codes: start with all 0s and then proceed by changing the least significant bit (LSB) which will bring about a new state. Advantages: fast, relatively free from errors.

44. Gray Codes Gray code is not unique, there are many possibilities to generate gray codes For example, G1={0=00 ， 1=01 ， 2=11 ， 3=10} G2={00=10 ， 1=11 ， 2=01 ， 3=00} Unique gray code: reflected Gray code

45. 從十進位 -> 反射葛雷碼 Source: 計算機概論 , 王孝熙 著 , 東華書局 .

46. 從反射葛雷碼 -> 十進位數字 Source: 計算機概論 , 王孝熙 著 , 東華書局 .

47. Floating-Point Representation Integers are fixed-point numbers in binary computers Floating-point literals are written with a decimal point: 8.5 -7.923 5.000 Real numbers are represented as “floating-point” numbers in binary system (all computers) The representation of floating-point numbers are various in different CPU In Intel 80486 CPU Single Precision: 32 bits Double Precision: 64 bits Extended Precision: 80bits

48. Floating-point literals Floating-point numbers may also be written in “scientific notation”– times a power of 10 We use E to represent “times 10 to the” Example: 4.32E5 means 4.32 x 10 5 http://www.nuvisionmiami.com/books/asm/workbook/floating_tut.htm

49. 範例 Source: 計算機概論 , 王孝熙 著 , 東華書局 .

50. Example

51. Binary Arithmetic on Numeric Data Binary addition Binary subtraction Binary multiplication Binary division To be discussed in Unit 5

52. Part II: Alphanumeric Data Alphanumeric data: character, letter, symbol, digit) Not for calculation, but for representation some “meanings” Coding ASCII(as-kee):America Standard Code for Information Interchange EBCDIC(eb-ce-dick):Extended Binary Coded Decimal Interchange Code (used by IBM, UNIVAC mainframes) BIG-5: for Chinese characters Uni-code

53. ASCII Code 7-bit for each character, 2 7 =128 combinations for 128 characters

54. Extended ACSII 8-bit for each character, 2 8 =256 combinations for 256 characters 。

55. Examples N: 4E=00101110 a: 61=01100001 t: 74=01110100 i: 69=01101001 o: 6F=01101111 n: 6E=01101110 a: 61=01100001 l: 6C=01101010

56. EBCDIC 8-bit for each character 4-bit Zone bits: identifying the code is for character, (un)signed number, or symbols 4-bit Digit bits: for numbers 0~9 。 http://www.natural-innovations.com/computing/asciiebcdic.html

58. Big5 Code Used for Chinese characters 1 character = 2 bytes (16 bits) Example

60. Unicode ASCII was very simplistic, and so was extended by adding 'extended' sets by various manufacturers. Apart from being confusing this was still restricted to 256 characters. Now computers are more widely established around the world the need to show other characters such as Japanese and Chinese languages along with various symbols became more important. 2 bytes (16-bit) for each unicode

61. Unicode samples

62. Binary Operations on Alphanumeric Data Binary addition? Binary subtraction? Binary multiplication? Binary division? To be discussed in Unit 5

63. Part III: Extensions Everything in the computer is stored as a pattern of bits Binary distinctions are easy for hardware to work with Numbers are stored as a pattern of bits Computers use the binary number system Characters are stored as a pattern of bits One byte (8 bits) can represent one of 256 characters So, is everything in the computer stored as a number? No it isn’t, it’s stored as a bit pattern There are many ways to interpret a bit pattern

64. Extension: Image representation Nature creations are analog, not digital Digitizing (sampling) Resolution: 800*600, 1026*768 Original 7*7 digitizing 14*14 digitizing

65. For Black/White Images Original 7*7 digitizing 14*14 digitizing 0000000 1111100 … 00000000000000 00000000000000 01111111110000 01111111111000 01111111111110 … 0000 0001 1111 00 … 0000 0000 0000 0000 0000 0000 0000 0111 1111 1100 0001 11111111100001111111111110… (01F0..) 2 (00000007FA1..) 2

66. For Colored Images

67. Extension: Sound Representation time AMP

68. Extension: Sampling Max. AMP/16 t 1 t 2 t 3 t 4 … 16=2 4 t 1 : 8=(1000) 2 t 2 : 9=(1001) 2 t 3 : 7=(0111) 2 t 4 : 2=(0010) 2 t 1 : 2=(0010) 2 … Quality vs sampling rate

69. Conclusion