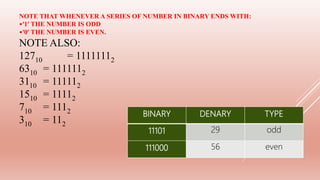
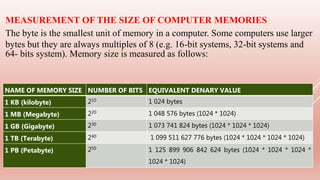
The document explains the fundamentals of binary computers, which operate using a binary numbering system (base 2) to transfer, store, and manipulate data through digital encoding of bits (0s and 1s). It covers the efficiency of binary logic, the advantages of bistable devices, and contrasts binary with decimal and hexadecimal systems, emphasizing the significance of various number bases in digital computing and data representation. Additionally, it discusses memory size measurements, differentiates between kilobytes and kibibytes, and provides examples of conversion between binary and decimal forms.

1. UNIT 1.1.1 - BINARY
Computers are digital, electronic machines that uses binary numbering
(base 2) system to transfer, store and manipulate data.
Binary numbers – Strings of 0's and 1's, are often associated with
computers.
Why is this and why can't computers just use base 10 instead of
converting to and from binary?
Is it more efficient to use a higher base, since binary (base 2)
representation uses up more "spaces"?

2. WHAT IS "DIGITAL"?
 Modern-day "digital" computer, operates on the principle of two possible
states of something – "on" and "off". The electronic circuit are of two
states or bistable using binary logic. Either 5 volts or 0 volts and this is
usually represented by binary digits ‘1’ (electrical current present) and ‘0’
(electrical current absent). The "on" state is assigned the value "1", while
the "off" state is assigned the value "0".
 Bistable devices are used in computers because they are cheap, quick,
reliable and take up only a small amount of space and energy. Moreover,
two distinct states provide a safety range for reliability.
 The term "binary" implies "two". Thus, the binary number system is a
system of numbers based on two possible digits – 0 and 1. This is where
the strings of binary digits come in. Each binary digit, or "bit", is a single 0
or 1, which directly corresponds to a single "switch" in a circuit. Add
enough of these "switches" together, and you can represent more numbers.
So instead of 1 digit, you end up with 8 to make a byte. (A byte, the basic
unit of storage, is simply defined as 8 bits; the well-known kilobytes,
megabytes, and gigabytes are derived from the byte, and each is 1,024
times as big as the other. There is a 1024-fold difference as opposed to a
1000-fold difference because 1024 is a power of 2 but 1000 is not.)

3. DOES BINARY USE MORE STORAGE THAN DECIMAL?
 On first glance, it seems like the binary representation of a number
10010110 uses up more space than its decimal (base 10)
representation 150. After all, the first is 8 digits long and the second
is 3 digits long. However, this is an invalid argument in the context
of displaying numbers on screen, since they're all stored in binary
regardless! The only reason that 150 is "smaller" than 10010110 is
because of the way we write it on the screen (or on paper).
 Increasing the base will decrease the number of digits required to
represent any given number, but taking directly from the previous
point, it is impossible to create a digital circuit that operates in any
base other than 2, since there is no state between "on" and "off"
(unless you get into quantum computers... more on this later).

4.  .WHAT ABOUT HEXADECIMAL & DIGITAL ENCODING?
 Hexadecimal (base 16) is simply a "shortcut" for representing binary
numbers. It is easier for the human programmer to represent a 32-bit
integer, often used for 32-bit color values, as FF00EE99 instead of
11111111000000001110111010011001
 All computer language and programming are based on the 2-digit
number system used in digital encoding.
 Digital encoding is the process of taking data and representing it with
discreet bits of information. These discreet bits consist of the 0s and
1s of the binary system.
 For example, images displayed on a computer screen have been
encoded with a binary line for each pixel. If a screen is using a 16-bit
code, then each pixel has been told what colour to display based on
which bits are 0s and which bits are 1s.
 As a result, 2^16 represents 65,536 different colours!
 All data stored in memory uses binary logic, where each binary digit
or bit can be set to ‘0’ and ‘1’.

5. THE NUMBER SYSTEM
A number system is a way to represent numbers.
•The denary (decimal) number system where the base is ten,
meaning we have combination of numbers between 0 to 9
{0,1,2,3,4,5,6,7,8,9}.
•The binary number system where the base is two, meaning we have
only two numbers {0 and 1}.
•The hexadecimal number system where the base is 16, meaning we
have combination of numbers between 0 to 15 {0, 1, 2, 3, 4, 5, 6, 7, 8,
9, A, B, C, D, E, F}.
Bases are represented as follows:
1011012 101101 base 2 (binary)
896510
8965 base 10 (denary)
7DB516
7DB5 base 16 (hexadecimal)

6. 100000 10000 1000 100 10 1
105 104 103 102 101 100
THE DENARY SYSTEM
Denary or decimal system is based on the number 10.
Some typical denary numbers would be: 58, 96, 80, 3956 etc.

7. 256 128 64 32 16 8 4 2 1
28 27 26 25 24 23 22 21 20
THE BINARY SYSTEM
It is based on the number 2.
Some typical binary number would be: 11010110, 011011, 1111000.
•Bit means binary digits ‘0’ and ‘1’.
•One Nibble is equal to 4 bits. {Examples: 0011, 1001, 1111, 1010}
•A Byte is a group of 8 bits (2 nibbles), it is used to represent a
character. {Examples: 1110 0011, 1001 1111, 10101100}

8. 65536 4096 256 16 1
164 163 162 161 160
THE HEXADECIMAL SYSTEM –
It is based on the number 16, referred to as simply ‘hex’ and therefore needs
to use 16 different ‘values’ to represent each digit.
The numbers 0 to 9 is the same as for the denary system and the letters A to F
are used to represent each hexadecimal (hex) digit.
(A = 10, B = 11, C = 12, D = 13, E = 14 and F = 15).
Some typical hexadecimal numbers would be: FF8B5, 1B0E, BACD,
59BFetc.

9.  CONVERTING DENARY TO BINARY
 EXAMPLE 1: Convert 2510 to binary

10.  EXAMPLE 2: Convert 6010 to binary

11.  CONVERTING BINARY TO DENARY
 EXAMPLE1: Convert 11011010 to denary
EXAMPLE2: Convert 10101110 to binary

12. BINARY DENARY TYPE
11101 29 odd
111000 56 even
NOTE THAT WHENEVER A SERIES OF NUMBER IN BINARY ENDS WITH:
•‘1’ THE NUMBER IS ODD
•‘0’ THE NUMBER IS EVEN.
NOTE ALSO:
12710 = 11111112
6310 = 1111112
3110 = 111112
1510 = 11112
710 = 1112
310 = 112

13. Manufacturers of storage devices often use the denary system to
measure storage size. For example,
1 kilobyte = 1 000 byte
1 megabyte = 1 000 000 bytes
1 gigabyte = 1 000 000 000 bytes
1 terabyte = 1 000 000 000 000 bytes and so on.
The IEC convention is now adopted by some organisations (including RAM) and
becomes:
1 kibibyte (1 KiB) = 1,024 bytes
1 mebibyte (1 MiB) = 1,048,576 bytes (1024 * 1024)
1 gibibyte (1 GiB) = 1,073,741,824 bytes (1024 * 1024 * 1024)
1 tebibyte (1 TiB) = 1,099,511,627,776 bytes and so on. (1024 * 1024 * 1024 *
1024)
However, the IEC terms are not universally used.

14. NAME OF MEMORY SIZE NUMBER OF BITS EQUIVALENT DENARY VALUE
1 KB (kilobyte) 210 1 024 bytes
1 MB (Megabyte) 220 1 048 576 bytes (1024 * 1024)
1 GB (Gigabyte) 230 1 073 741 824 bytes (1024 * 1024 * 1024)
1 TB (Terabyte) 240 1 099 511 627 776 bytes (1024 * 1024 * 1024 * 1024)
1 PB (Petabyte) 250
1 125 899 906 842 624 bytes (1024 * 1024 * 1024 *
1024 * 1024)
MEASUREMENT OF THE SIZE OF COMPUTER MEMORIES
The byte is the smallest unit of memory in a computer. Some computers use larger
bytes but they are always multiples of 8 (e.g. 16-bit systems, 32-bit systems and
64- bits system). Memory size is measured as follows:

15. WHAT IS THE DIFFERENCE BETWEEN KIBIBYTE AND KILOBYTE?
A kilobyte is decimal representation that uses
the kilo prefix, which means 1000 times
something. 1 KB is 1000 bytes.
A kibibyte is binary representation that uses the
kibi prefix, which means 1024 times something.
1 KiB is 1024 bytes.

16. SOME TYPICAL EXAM TYPE QUESTIONS
 1 a) Express 95 denary as an 8-bit
binary number.
 Answer will be: 0101 1111
 b) Change the binary number1100 1101
into a denary integer.
 Answer will be: 109
 C) Give two uses for a binary number.
 In sound, to store instruction, part of an
image, in ASCII value/ Unicode, in
registers etc.
128 64 32 16 8 4 2 1
0 1 0 1 1 1 1 1
 •(d) Explain the differences between
the binary number system and the
denary number system.
 A binary number system is a base-2
system while denary number system
is a base-10 system
 A binary number system uses 0 and 1
values while a denary number system
uses 0 to 9 values
 Binary has more digit for the same
value while denary has less digits for
the same value

17.  2 (a) Explain the process of converting
the binary number 1101 into a denary
number.
 We construct a table and input
values in the table that we multiply
as depicted below;
 We multiply each binary value to the
corresponding value in the first row
and add them.
 (1 * 8) + (1 * 4) + (0 * 2) + (1 * 1)
 Answer is 13
b)Complete the sentences using the
list given below. Not all items in the
list need to be used.
Human are more used to the
manipulate data in ………..…………
form which is in base ………………..,
but for a computer to process data it
needs to be converted to
…………………… form that is base
…………………...
A number system that is easier for
the human programmer abbreviated
as hex is the …………..…………. System
that and its base is ……………………..
 Answer as follows: denary, 10,
binary, 2, hexadecimal, 16
10 Binary Hexadecimal
2 denary 16
8 4 2 1
1 1 0 1

18. 3. You may get questions to interpret
the time in a clock, floor lift, car
dash board etc.
 a) The time in a digital clock is
displayed as follows:
 Convert it into 4-bits binary. The
answer will be:
b) You may be given a series of binary to
interpret the time. Example:
The answer would be: 23:59
c) You may also be asked to explain how the
microprocessor will sound at alarm at for
example 06.00.
The microprocessor will compared the
actual time to the alarm time set. If the
actual time and the alarm time matches, the
alarm will activate.
0 9 4 8
0 0000
9 1001
4 0100
8 1000
0010 0011 0101 1001
0010 2
0011 3
0101 5
1001 9