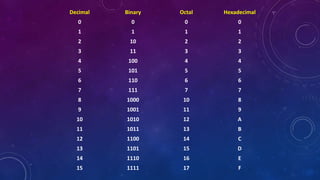
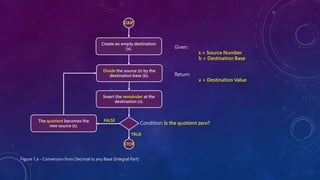
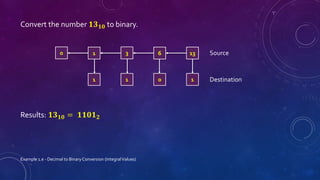
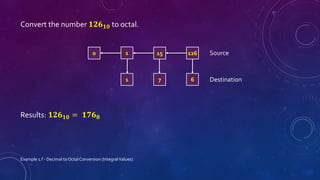
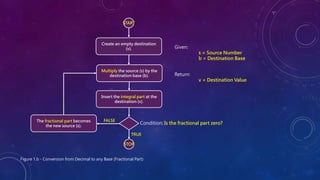
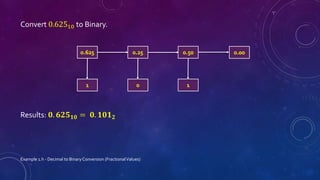
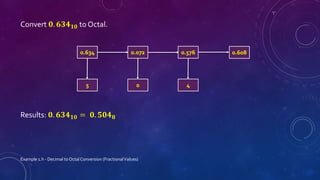
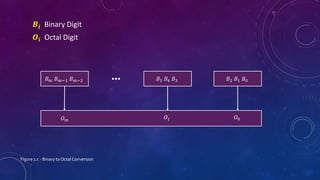
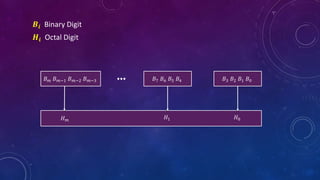
This document discusses different number systems including positional and non-positional. It describes the decimal, binary, octal, and hexadecimal number systems. For each system it provides the base, symbols used, an example of a number written in that system and its equivalent decimal value, and explanations of how positional notation works. It also provides steps and examples for converting between decimal, binary, octal, and hexadecimal numbers for both integral and fractional values.

1. NUMBER SYSTEMS & DATA
REPRESENTATIONS
FUNDAMENTALS OF COMPUTER & PROGRAMMING (COMP 1)
PREPARED BY: PHILLIP GLENN LIBAY

2. NUMBER SYSTEM

3. NUMBER SYSTEM
Is a method of expressing values, using a set of symbols in a
consistent manner.
Several number systems has been used in the past which can be
categorized into two (2): positional and non-positional number
systems.

4. POSITIONAL NUMBER SYSTEM

5. POSITIONAL NUMBER SYSTEM
In a positional number system, the position the symbol occupies
determines the value it represents, thus, it is also often called the
PLACE VALUE system.

6. HOW DOES IT WORKS?
If number is represented as:
± 𝒔 𝒏−𝟏 ⋯ 𝒔 𝟏 𝒔 𝟎 . 𝒔−𝟏 𝒔−𝟐 ⋯ 𝒃
Then it has the value of:
𝒗 = ± 𝒔 𝒏−𝟏 × 𝒃 𝒏−𝟏 + ⋯ + 𝒔 𝟏 × 𝒃 𝟏 + 𝒔 𝟎 × 𝒃 𝟎 + 𝒔−𝟏 × 𝒃−𝟏 + 𝒔−𝟐 × 𝒃−𝟐 + ⋯

7. DECIMAL number system

8. DECIMAL NUMBER SYSTEM
• Is a number system with the base of 10.
• It uses ten (10) unique symbols to represent values.
0 1 2 3 4 5 6 7 8 9

9. 1. 𝟏𝟐𝟑 𝟏𝟎
• n = 3, b = 10
• 1 × 102 + 2 × 101 + 3 × 100
• 1 × 100 + 2 × 10 + (3 × 1)
• 100 + 20 + 3
• The equivalent decimal number is One Hundred Twenty
Example 1.a - Decimal Number System, Positional Values

10. BINARY number system

11. BINARY NUMBER SYSTEM
• Is a number system with the base of 2.
• It uses two (2) unique symbols to represent values.
0 1

12. 1. 𝟏𝟎𝟎𝟏 𝟐
• n = 4, b = 2
• 1 × 23 + 0 × 22 + 0 × 21 + 1 × 20
• 1 × 8 + 0 × 4 + 0 × 2 + (1 × 1)
• 8 + 0 + 0 + 1
• The equivalent decimal number is Nine
Example 1.b - Binary Number System, Positional Values

13. OCTAL number system

14. OCTAL NUMBER SYSTEM
• Is a number system with the base of 8.
• It uses eight (8) unique symbols to represent values.
0 1 2 3 4 5 6 7

15. 1. 𝟏𝟐𝟕 𝟖
• n = 3, b = 8
• 1 × 82 + 2 × 81 + 7 × 80
• 1 × 64 + 2 × 8 + 7 × 1
• 64 + 16 + 7
• So the equivalent decimal number is Eighty Seven
Example 1.c - Octal Number System, Positional Values

16. HEXADECIMAL number system

17. HEXADECIMAL NUMBER SYSTEM
• Is a number system with the base of 16.
• It uses sixteen (16) unique symbols to represent values.
0 1 2 3 4 5 6 7 8 9 A B C D E F

18. 1. 𝑨𝟏𝟗 𝟏𝟔
• n = 3, b = 16
• 𝐴 × 162 + 1 × 161 + 9 × 160
• 10 × 256 + 1 × 16 + 9 × 1
• 256 + 16 + 9
• So the equivalent decimal number is Two Hundred Eighty
Example 1.d - Hexadecimal Number System, Positional Values

19. Decimal Binary Octal Hexadecimal
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F

20. DECIMAL to BASE n conversions

21. START
Create an empty destination
(v).
Divide the source (s) by the
destination base (b).
Insert the remainder at the
destination (v).
STOP
The quotient becomes the
new source (s).
TRUE
FALSE
Condition: Is the quotient zero?
Given:
s = Source Number
b = Destination Base
Return:
v = Destination Value
Figure 1.a - Conversion from Decimal to any Base (Integral Part)

22. DECIMAL TO BINARY conversion
INTEGRAL VALUES

23. Convert the number 𝟏𝟑 𝟏𝟎 to binary.
Results: 𝟏𝟑 𝟏𝟎 = 𝟏𝟏𝟎𝟏 𝟐
Example 1.e - Decimal to Binary Conversion (IntegralValues)
1361 30
1011
Source
Destination

24. DECIMAL TO OCTAL conversion
INTEGRAL VALUES

25. Example 1.f - Decimal to Octal Conversion (IntegralValues)
Convert the number 𝟏𝟐𝟔 𝟏𝟎 to octal.
Results: 𝟏𝟐𝟔 𝟏𝟎 = 𝟏𝟕𝟔 𝟖
126150 1
671
Source
Destination

26. DECIMAL TO HEXADECIMAL conversion
INTEGRAL VALUES

27. Example 1.g - Decimal to Hexadecimal Conversion (IntegralValues)
Convert the number 𝟏𝟐𝟔 𝟏𝟎 to octal.
Results: 𝟏𝟐𝟔 𝟏𝟎 = 𝟕𝑬 𝟏𝟔
12670
E7
Source
Destination

28. START
Create an empty destination
(v).
Multiply the source (s) by the
destination base (b).
Insert the integral part at the
destination (v).
STOP
The fractional part becomes
the new source (s).
TRUE
FALSE
Condition: Is the fractional part zero?
Given:
s = Source Number
b = Destination Base
Return:
v = Destination Value
Figure 1.b - Conversion from Decimal to any Base (Fractional Part)

29. DECIMAL TO BINARY conversion
FRACTIONAL VALUES

30. Convert 0.62510 to Binary.
Results: 𝟎. 𝟔𝟐𝟓 𝟏𝟎 = 𝟎. 𝟏𝟎𝟏 𝟐
Example 1.h - Decimal to Binary Conversion (FractionalValues)
0.625 0.25 0.50 0.00
1 0 1

31. DECIMAL TO OCTAL conversion
FRACTIONAL VALUES

32. Convert 𝟎. 𝟔𝟑𝟒 𝟏𝟎 to Octal.
Results: 𝟎. 𝟔𝟑𝟒 𝟏𝟎 = 𝟎. 𝟓𝟎𝟒 𝟖
Example 1.h - Decimal to Octal Conversion (FractionalValues)
0.634 0.072 0.576 0.608
5 0 4

33. DECIMAL TO HEXADECIMAL conversion
FRACTIONAL VALUES

34. Convert 𝟎. 𝟔𝟒 𝟏𝟎 to Hexadecimal.
Results: 𝟎. 𝟔𝟒 𝟏𝟎 = 𝟎. 𝑨𝟑𝑫 𝟏𝟔
Example 1.h - Decimal to Hexadecimal Conversion (FractionalValues)
0.64 0.24 0.84 0.44
A 3 D

35. BINARY to OCTAL conversion

36. 𝑩𝒊 Binary Digit
𝑶𝒊 Octal Digit
Figure 1.c - Binary to Octal Conversion
𝐵 𝑚 𝐵 𝑚−1 𝐵 𝑚−2 𝐵5 𝐵4 𝐵3 𝐵2 𝐵1 𝐵0
…
𝑂 𝑚
𝑂1 𝑂0

37. BINARY to HEXADECIMAL conversion

38. 𝑩𝒊 Binary Digit
𝑯𝒊 Octal Digit
𝐵 𝑚 𝐵 𝑚−1 𝐵 𝑚−2 𝐵 𝑚−3 𝐵7 𝐵6 𝐵5 𝐵4 𝐵3 𝐵2 𝐵1 𝐵0
…
𝐻 𝑚
𝐻1 𝐻0

39. OCTAL to HEXADECIMAL conversion

40. 𝐻2 𝐻1 𝐻0
1 0 0 1 1 0 1 0 1 0 1 0
𝑂3 𝑂2 𝑂1 𝑂0