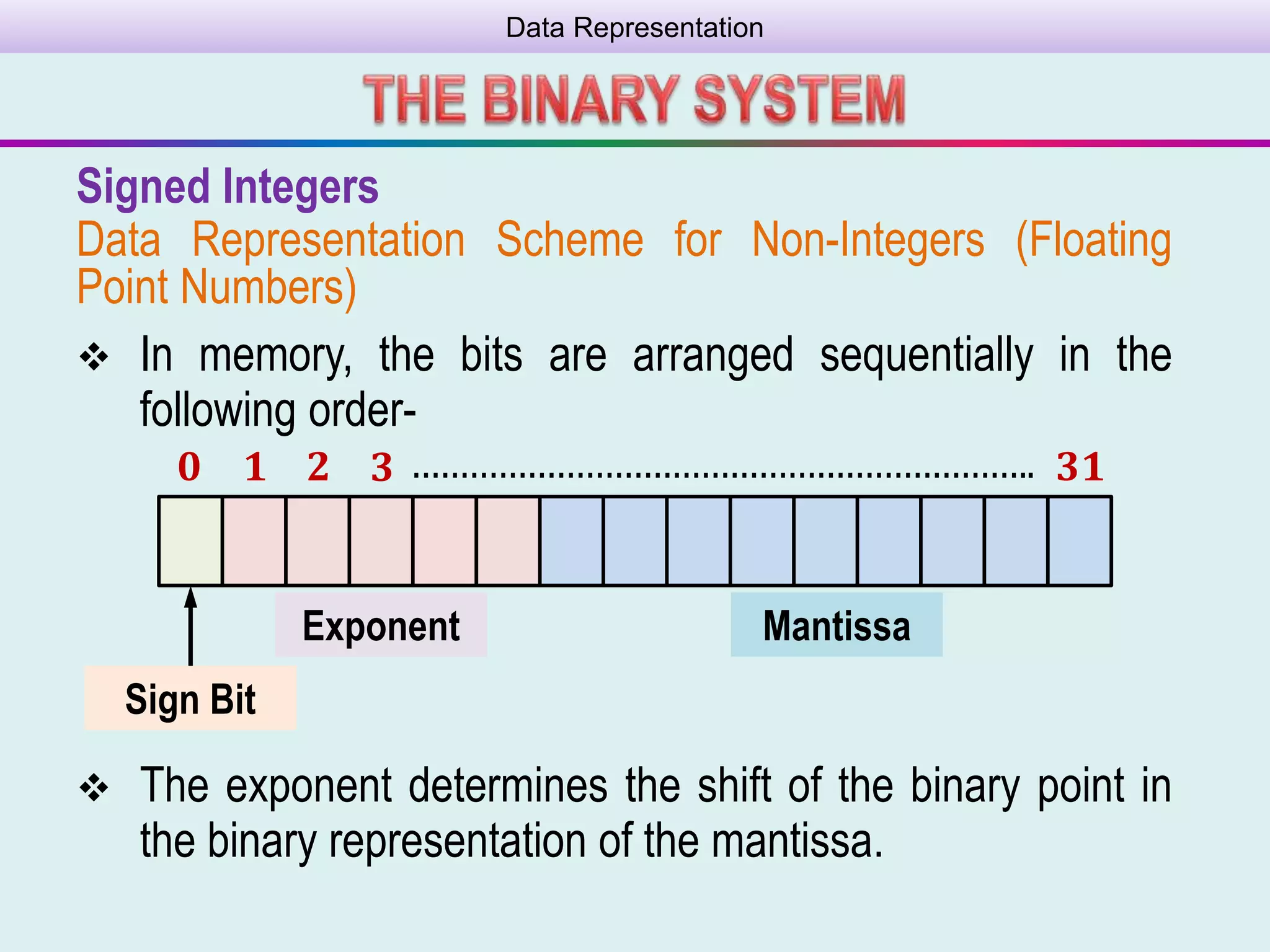
The document discusses how data is represented in computers using binary numbers. It explains that computers use binary, which represents numbers using only two digits (0 and 1) rather than the decimal system's ten digits. This binary system maps well to the two states of on/off in a computer's electrical circuits. The document provides examples of converting decimal numbers to binary and vice versa. It also discusses how signed integers and floating point numbers are represented using binary.

1. Department of Civil Engineering
Chittagong University of Engineering & Technology
Sanjoy Das
Lecturer
CE 218
Computer Programming Sessional

2. Data Representation
 In our familiar number system we have 𝟏𝟎 symbols (𝟎 to
𝟗) to represent a number.
 We call it decimal system or 𝟏𝟎 base system.
 To process data in a computer, we need to represent
them in the registers of the processor.
 A register consists of several circuits.

3. Data Representation
 Can we represent 10 symbols using an electric circuit?
Obviously no.
 We can symbolize an electric circuit into two states such
as-
(a) contains current (1)
(b) no current(0)
 Similarly for a magnetic media such as a disk we may
consider two states-
(a) magnetized clockwise
(b) magnetized counterclockwise

4. Data Representation
 We may think these two states as two symbols (say one
is 𝟎 and the other is 𝟏) to represent a number.
 Thus we have only two digitsto represent a number in
the computer processor, in the memory or in the data
storage devices.
 Each individual circuit represents a digit and we term it as
a bit (it is an abbreviation from binary digit).
 Thus, at circuit level, we can represent a number in the
computer in binary form.

5. Data Representation
 Computers work with the binary or base-two system of
numbers that uses the two digits 𝟎 and 𝟏 instead of the
ten digits 𝟎 – 𝟗 of the more familiar decimal or base-ten
system.
 In the binary system, a number is denoted as-
𝒃 𝒌 𝒃 𝒌−𝟏 … … 𝒃 𝟎 𝒃−𝟏 … … 𝒃−𝒍 𝟐 (1)
 Where 𝒌 and 𝒍 are two integer indices.
 The binary digits or bits, 𝒃𝒊 take the value of 𝟎 or 𝟏, and
the period (.) is the binary point.

6. Data Representation
 The implied value is equal to-
𝒃 𝒌 × 𝟐 𝒌 + 𝒃 𝒌−𝟏 × 𝟐 𝒌−𝟏 + ⋯ + 𝒃 𝟎 × 𝟐 𝟎
+𝒃−𝟏 × 𝟐−𝟏 + ⋯ 𝒃−𝒍 × 𝟐−𝒍 (2)
 Where 𝒎 and 𝒏 are two integer indices.
 The decimal digits, 𝒅𝒊 take values in the range 𝟎 − 𝟏,
and the period (.) is the decimal point.
 In the decimal system, the same number is expressed
as-
𝒅 𝒎 𝒅 𝒎−𝟏 … … 𝒅 𝟎 𝒅−𝟏 … … 𝒅−𝒏 𝟏𝟎 (3)

7. Data Representation
 The implied value is equal to-
𝒅 𝒎 × 𝟏𝟎 𝒎 + 𝒅 𝒎−𝟏 × 𝟏𝟎 𝒎−𝟏 + ⋯ + 𝒅 𝟎 × 𝟏𝟎 𝟎
+𝒅−𝟏 × 𝟏𝟎−𝟏 + ⋯ 𝒅−𝒏 × 𝟏𝟎−𝒏 (4)
 Which is identical to that computed from the base-two
expansion.
 Since bits can be represented by the on-off positions of
electrical switches that are built in the computer’s
electrical circuitry, and since bits can be transmitted by
positive or negative voltage as a Morse code, the
binary system is ideal for developing a computer
architecture.

8. Data Representation
Conversion from Decimal to Binary
 The conversion from a decimal number to a binary
number can be explained by the following example-
𝟓𝟐𝟎𝟖 𝟏𝟎 = 𝟏𝟎𝟏𝟎𝟎𝟎𝟏𝟎𝟏𝟏𝟎𝟎𝟎 𝟐
𝟐 𝟓𝟐𝟎𝟖
𝟐 𝟐𝟔𝟎𝟒 − 𝟎
𝟐 𝟏𝟑𝟎𝟐 − 𝟎
𝟐 𝟔𝟓𝟏 − 𝟎
𝟐 𝟑𝟐𝟓 − 𝟏
𝟐 𝟏𝟔𝟐 − 𝟏
𝟐 𝟖𝟏 − 𝟎
𝟐 𝟒𝟎 − 𝟏
𝟐 𝟐𝟎 − 𝟎
𝟐 𝟏𝟎 − 𝟎
𝟐 𝟓 − 𝟎
𝟐 𝟐 − 𝟏
𝟏 − 𝟎

9. Data Representation
Conversion from Decimal to Binary
 The conversion from a decimal number (non - integer) to
a binary number can be explained by the following
example-
𝟑𝟒𝟓. 28125 𝟏𝟎 = 𝟏𝟎𝟏𝟎𝟏𝟏𝟎𝟎𝟏. 𝟎𝟏𝟎𝟎𝟏 𝟐
𝟐 𝟑𝟒𝟓
𝟐 𝟏𝟕𝟐 − 𝟏
𝟐 𝟖𝟔 − 𝟎
𝟐 𝟒𝟑 − 𝟎
𝟐 𝟐𝟏 − 𝟏
𝟐 𝟏𝟎 − 𝟏
𝟐 𝟓 − 𝟎
𝟐 𝟐 − 𝟏
𝟏 − 𝟎
𝟎. 𝟐𝟖𝟏𝟐𝟓 × 𝟐 = 𝟎. 𝟓𝟔𝟐𝟓
𝟎. 𝟓𝟔𝟐𝟓𝟎 × 𝟐 = 𝟏. 𝟏𝟐𝟓𝟎
𝟎. 𝟏𝟐𝟓𝟎𝟎 × 𝟐 = 𝟎. 𝟐𝟓𝟎𝟎
𝟎. 𝟐𝟓𝟎𝟎𝟎 × 𝟐 = 𝟎. 𝟓𝟎𝟎𝟎
𝟎. 𝟓𝟎𝟎𝟎𝟎 × 𝟐 = 𝟏. 𝟎𝟎𝟎𝟎

10. Data Representation
Conversion from Binary to Decimal
 The conversion from a binary number to a decimal
number can be explained by the following example-
𝟏𝟎𝟏𝟎𝟎𝟎𝟏𝟎𝟏𝟏𝟎𝟎𝟎 𝟐 = 𝟓𝟐𝟎𝟖 𝟏𝟎
𝟎 × 𝟐 𝟎
= 𝟎
𝟎 × 𝟐 𝟏
= 𝟎
𝟎 × 𝟐 𝟐
= 𝟎
𝟏 × 𝟐 𝟑
= 𝟖
𝟏 × 𝟐 𝟒
= 𝟏𝟔
𝟎 × 𝟐 𝟓
= 𝟎
𝟏 × 𝟐 𝟔
= 𝟔𝟒
𝟎 × 𝟐 𝟕
= 𝟎
𝟎 × 𝟐 𝟖
= 𝟎
𝟎 × 𝟐 𝟗
= 𝟎
𝟏 × 𝟐 𝟏𝟎
= 𝟏𝟎𝟐𝟒
𝟎 × 𝟐 𝟏𝟏
= 𝟎
𝟏 × 𝟐 𝟏𝟐
= 𝟒𝟎𝟗𝟔
𝟓𝟐𝟎𝟖

11. Data Representation
Conversion from Binary to Decimal
 The conversion from a binary number (non – integer) to a
decimal number can be explained by the following
example-
𝟏𝟎𝟏𝟎𝟏𝟏𝟎𝟎𝟏. 𝟎𝟏𝟎𝟎𝟏 𝟐 = 𝟑𝟒𝟓. 28125 𝟏𝟎
𝟏 × 𝟐 𝟎
= 𝟏
𝟎 × 𝟐 𝟏
= 𝟎
𝟎 × 𝟐 𝟐
= 𝟎
𝟏 × 𝟐 𝟑
= 𝟖
𝟏 × 𝟐 𝟒
= 𝟏𝟔
𝟎 × 𝟐 𝟓
= 𝟎
𝟏 × 𝟐 𝟔
= 𝟔𝟒
𝟎 × 𝟐 𝟕
= 𝟎
𝟏 × 𝟐 𝟖
= 𝟐𝟓𝟔
𝟎 × 𝟐−𝟏
= 𝟎
𝟏 × 𝟐−𝟐
= 𝟎. 𝟐𝟓
𝟎 × 𝟐−𝟑
= 𝟎
𝟎 × 𝟐−𝟒
= 𝟎
𝟏 × 𝟐−𝟓
= 𝟎. 𝟎𝟑𝟏𝟐𝟓
𝟑𝟒𝟓
𝟎. 𝟐𝟖𝟏𝟐𝟓

12. Data Representation
The Largest Integer Encoded by 𝐩 Bits
 Each individual circuit represents a digit and we term it
as a bit (it is an abbreviation from binary digit).
 As you all know, the largest number for a given number of
digits can be obtained by filling out each position with the
largest symbol.
 Such as :
 in decimal, largest number with 3 digits = 999
 similarly, in binary, largest number with 3 digits = 111

13. Data Representation
The Largest Integer Encoded by 𝐩 Bits
 So, the largest integer that can be represented with 𝐩
bits is-
𝟏𝟏𝟏 … 𝟏𝟏𝟏 𝟐 (5)
 Where the ones are repeated 𝐩 times.
 The decimal - number equivalent is-
𝟏 × 𝟐 𝒑−𝟏 + 𝟏 × 𝟐 𝒑−𝟐 + 𝟏 × 𝟐 𝒑−𝟑 + ⋯
+𝟏 × 𝟐 𝟐
+ 𝟏 × 𝟐 𝟏
+ 𝟏 × 𝟐 𝟎
= 𝟐 𝒑
− 𝟏(6)

14. Data Representation
The Largest Integer Encoded by 𝐩 Bits
 To demonstrate this equivalence, we recall from our
college years-
 Where 𝒂 and 𝒃 are two variables and set 𝒂 = 𝟐and
𝒃 = 𝟏.
𝒂 𝒑 − 𝒃 𝒑 = (𝒂 − 𝒃)(𝒂 𝒑−𝟏 + 𝒂 𝒑−𝟐 𝒃 + ⋯ 𝒂𝒃 𝒑−𝟐 + 𝒃 𝒑−𝟏)(7)

15. Data Representation
The Largest Integer Encoded by 𝐩 Bits
 When one bit is available, we can describe only the
integers 𝟎 and 𝟏, and the largest integer is 𝟏.
 With two bits the maximum is 𝟐 𝟐 − 𝟏 = 𝟑.
 With three bits the maximum is 𝟐 𝟑 − 𝟏 = 𝟕.
 With eight bits the maximum is 𝟐 𝟖 − 𝟏 = 𝟐𝟓𝟓.
 With thirty-onebits the maximum is
𝟐 𝟑𝟏
− 𝟏 = 𝟐𝟏𝟒𝟕𝟒𝟖𝟑𝟔𝟒𝟕.

16. Data Representation
Signed Integers
 To encode a signed integer, we allocate the first bit to
the sign.
 If the leading bit is 𝟎, the integer is positive; if the
leading bit is 𝟏, the integer is negative.
 The largest signed integer that can be represented with 𝐩
bits is then-
 According to this convention, the integer − 𝟓 = − 𝟏𝟎𝟏 𝟐
is stored as the binary string 𝟏𝟏𝟎𝟏.

17. Data Representation
Signed Integers
Data Representation Scheme for Integers
………………………………………………………..𝟎 𝟏 𝟐 𝟑 𝟑𝟏
Sign Bit
………………………………………………………..
1 1 0 1
𝟎 𝟏 𝟐 𝟑 𝟑𝟏
Sign Bit
− 𝟓 = − 𝟏𝟎𝟏 𝟐
is stored as the binary string 𝟏𝟏𝟎𝟏

18. Data Representation
Signed Integers
Data Representation Scheme for Non-Integers (Floating
Point Numbers)
 The floating-point representation allows us to store real
numbers (non-integers) with a broad range of
magnitudes, and carry out mathematical operations
between numbers with disparate magnitudes.

19. Data Representation
Signed Integers
Data Representation Scheme for Non-Integers (Floating
Point Numbers)
 Consider the binary number-
𝟏𝟎𝟎𝟏𝟏𝟎𝟎𝟏𝟎𝟏. 𝟎𝟏𝟏𝟎𝟎𝟎𝟏𝟏𝟏𝟎𝟏
 To develop the floating-point representation, we recast
this number into the product-
𝟏. 𝟎𝟎𝟏𝟏𝟎𝟎𝟏𝟎𝟏𝟎𝟏𝟏𝟎𝟎𝟎𝟏𝟏𝟏𝟎𝟏 × 𝟏𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎
 Note that the binary point has been shifted to the left by
nine places, and the resulting number has been
multiplied by the binary equivalent of 𝟐 𝟗
.
 The binary string 𝟏𝟎𝟎𝟏𝟏𝟎𝟎𝟏𝟎𝟏𝟎𝟏𝟏𝟎𝟎𝟎𝟏𝟏𝟏𝟎𝟏 is the
mantissa or significand, and 𝟗is the exponent.

20. Data Representation
Signed Integers
Data Representation Scheme for Non-Integers (Floating
Point Numbers)
 To develop the floating-point representation of an
arbitrary number, we express it in the form-
 Where 𝒔 is a real number called the mantissa or
significand, and 𝒆 is the integer exponent.
 This representation requires one bit for the sign, a set
of bytes for the exponent, and another set of bytes
for the mantissa.
±𝒔 × 𝟐 𝒆 (9)

21. Data Representation
Signed Integers
Data Representation Scheme for Non-Integers (Floating
Point Numbers)
 In memory, the bits are arranged sequentially in the
following order-
 The exponent determines the shift of the binary point in
the binary representation of the mantissa.
………………………………………………………..𝟎 𝟏 𝟐 𝟑 𝟑𝟏
Sign Bit
Exponent Mantissa

22. • For a 32-bit float type, the mantissa is stored in a
23-bit segment and the exponent in an 8-bit
segment, leaving 1 bit for the sign of the number.
For a 64-bit double type, the mantissa is stored in
a 52-bit segment and the exponent in an 11-bit
segment.
Data Representation