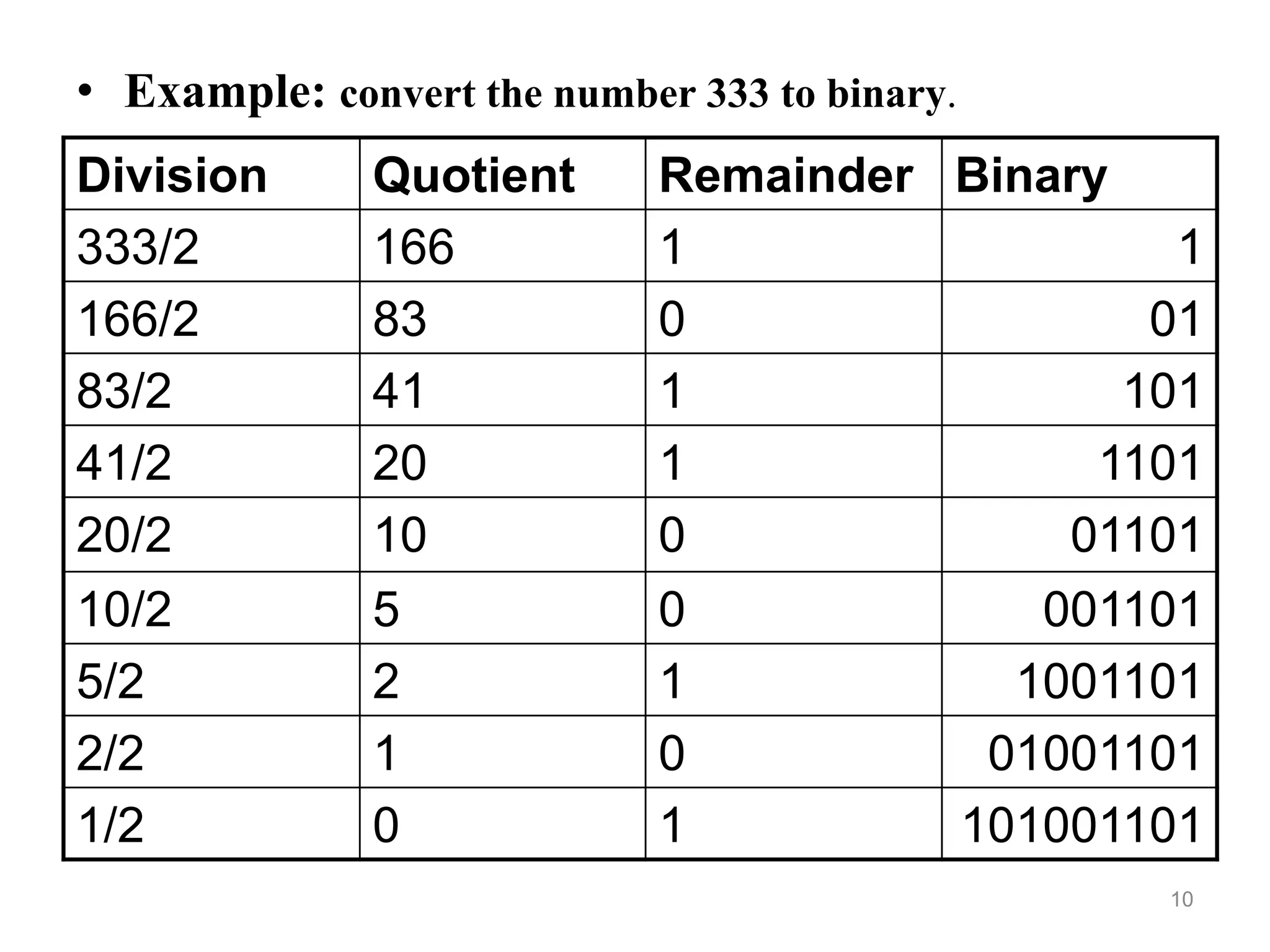
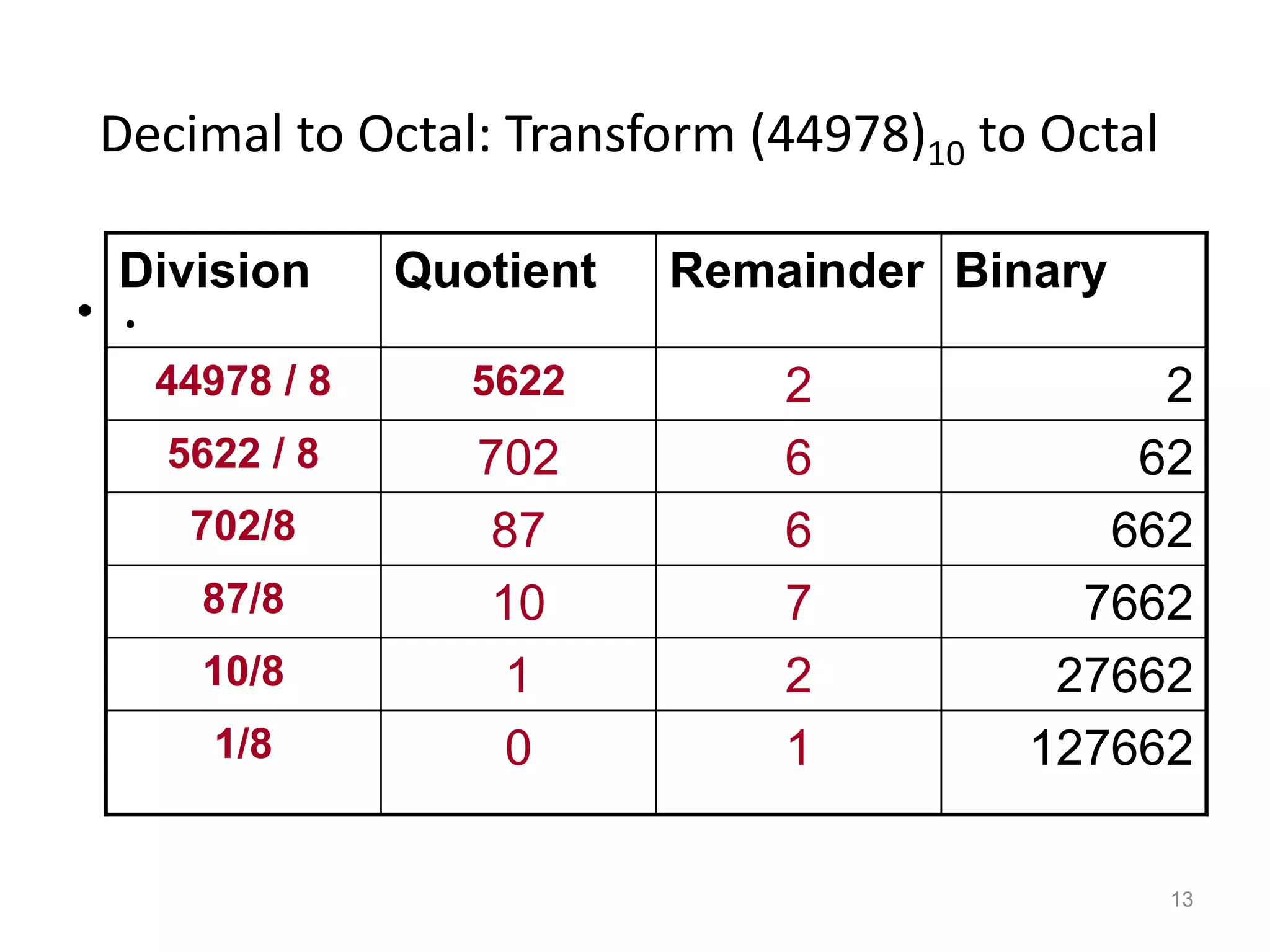
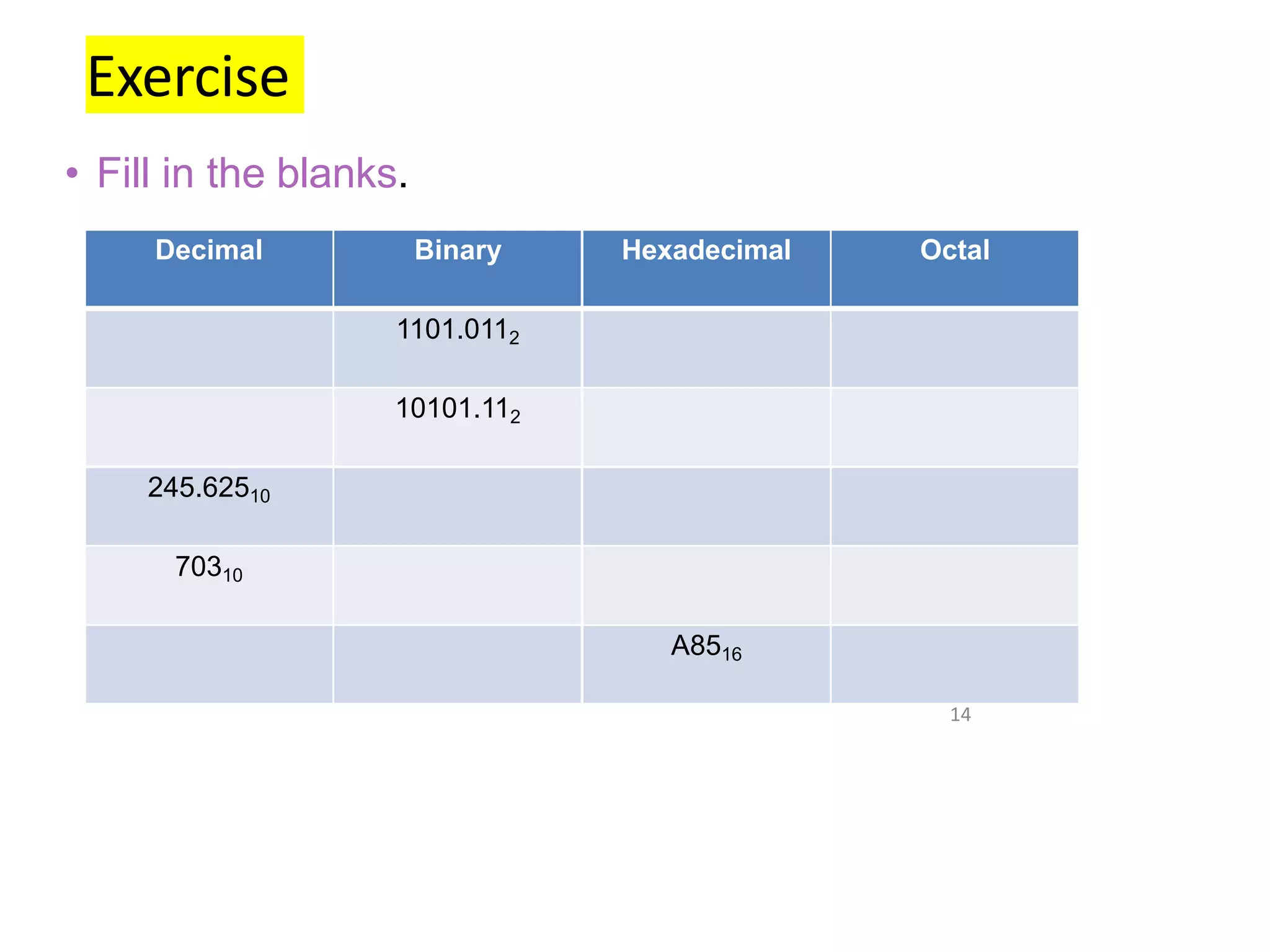
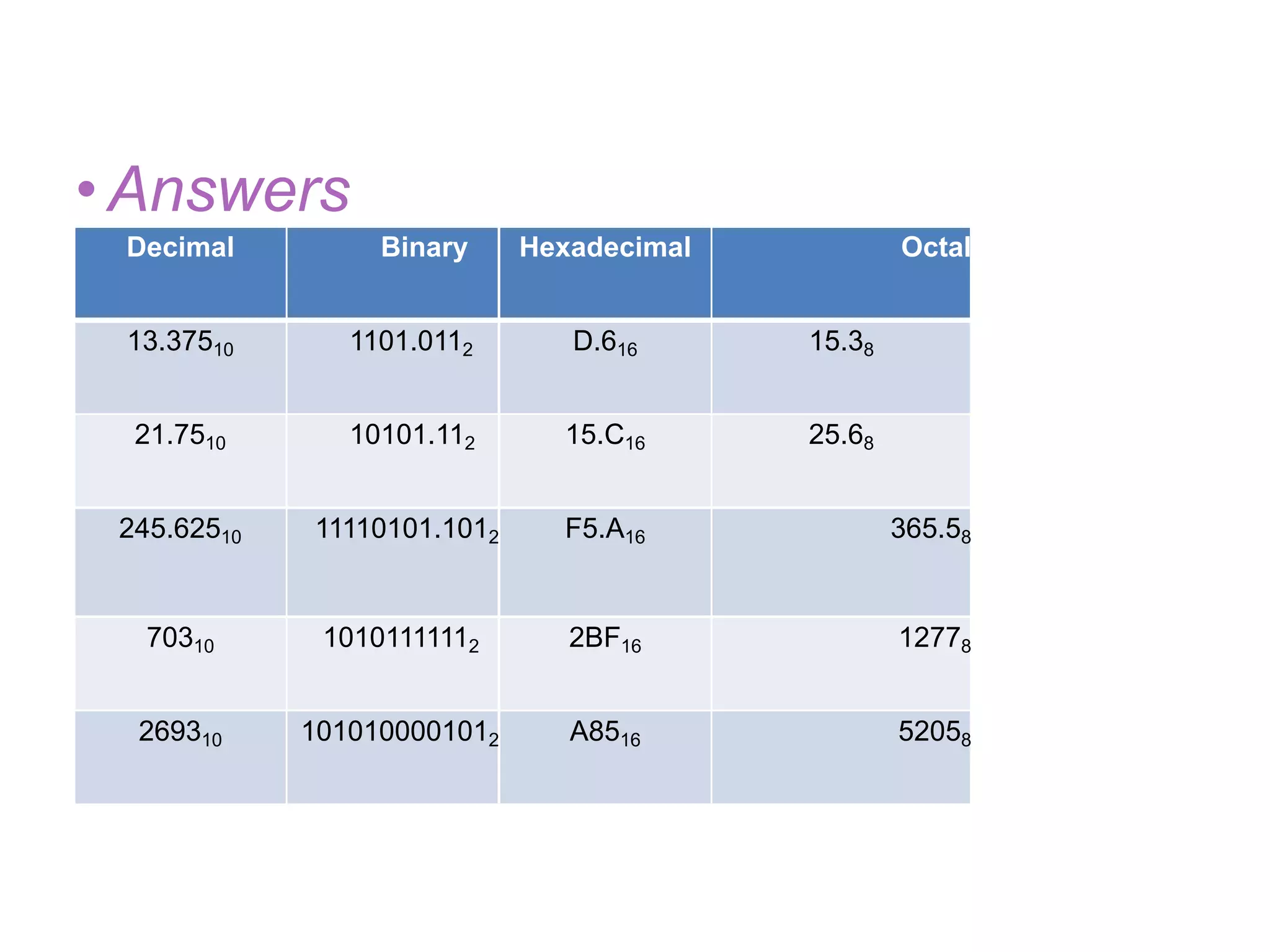
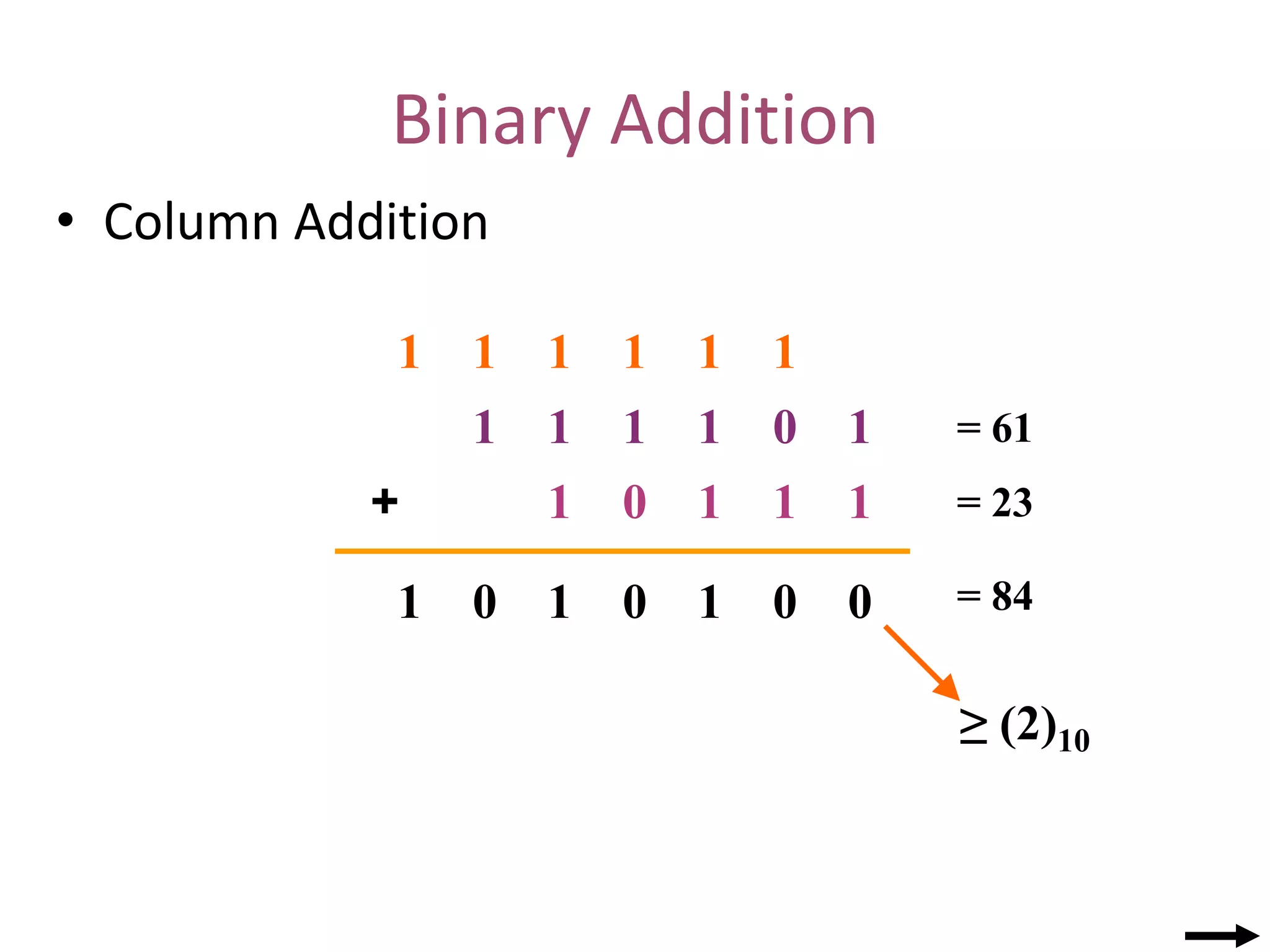
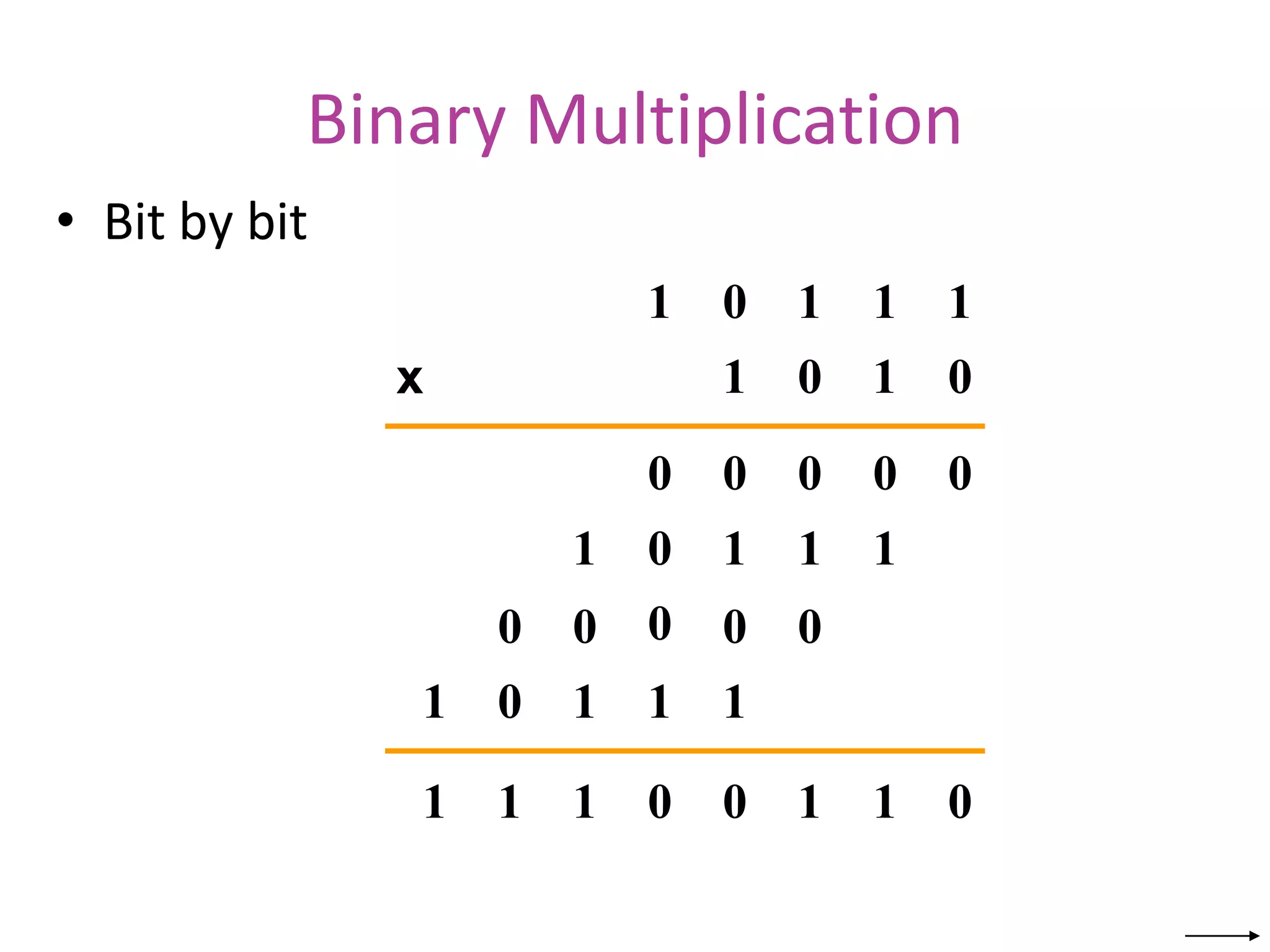
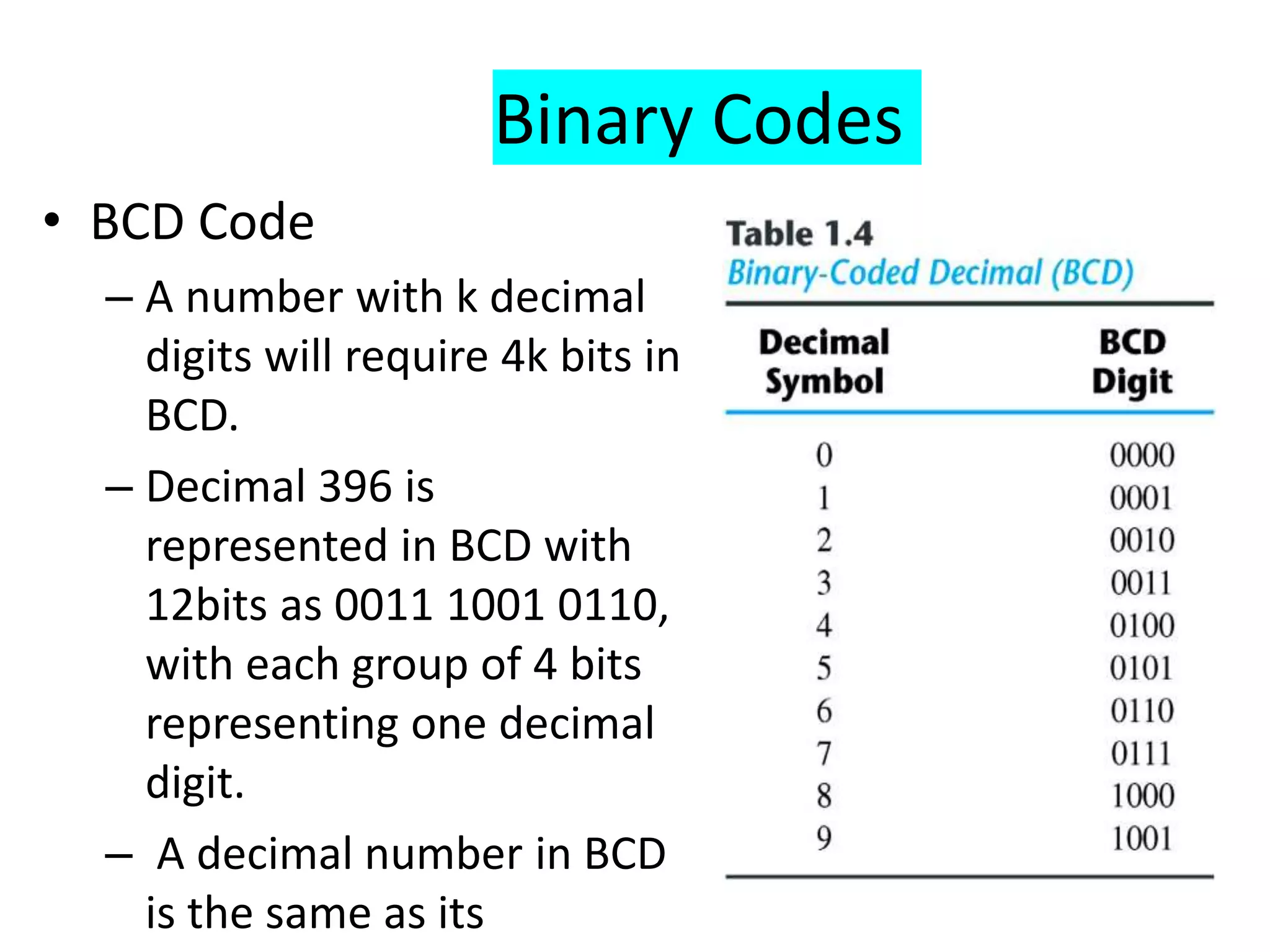
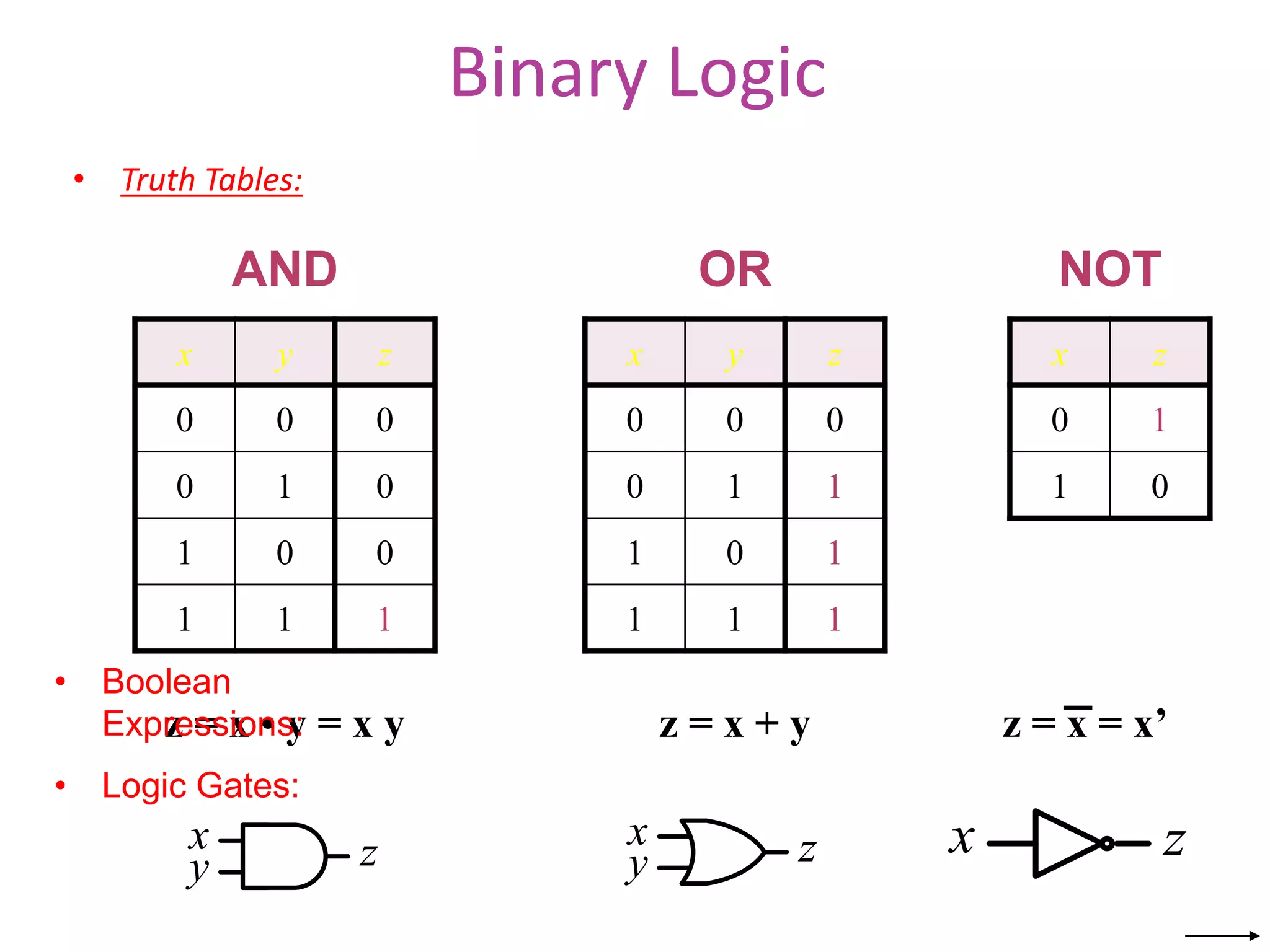
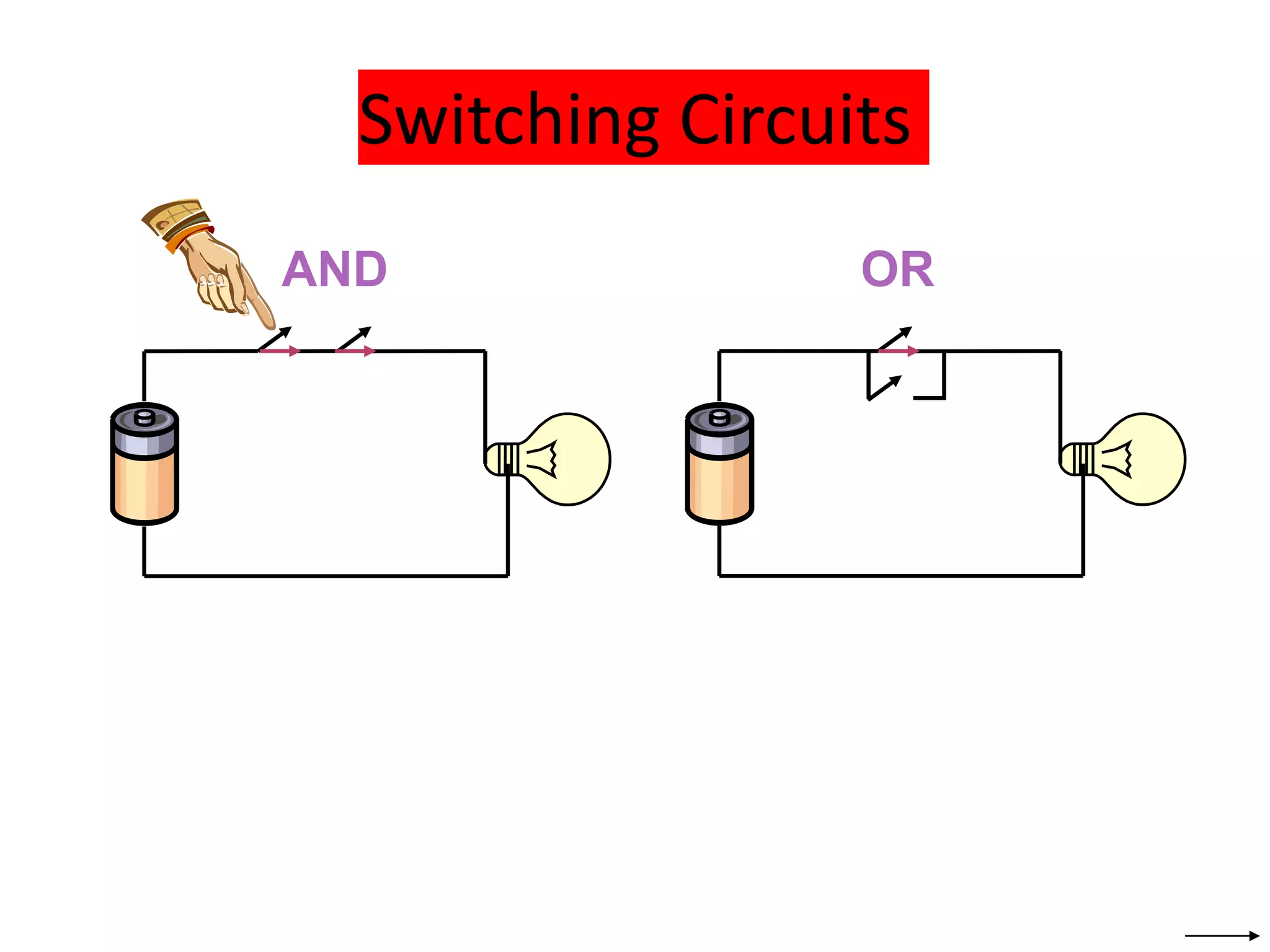
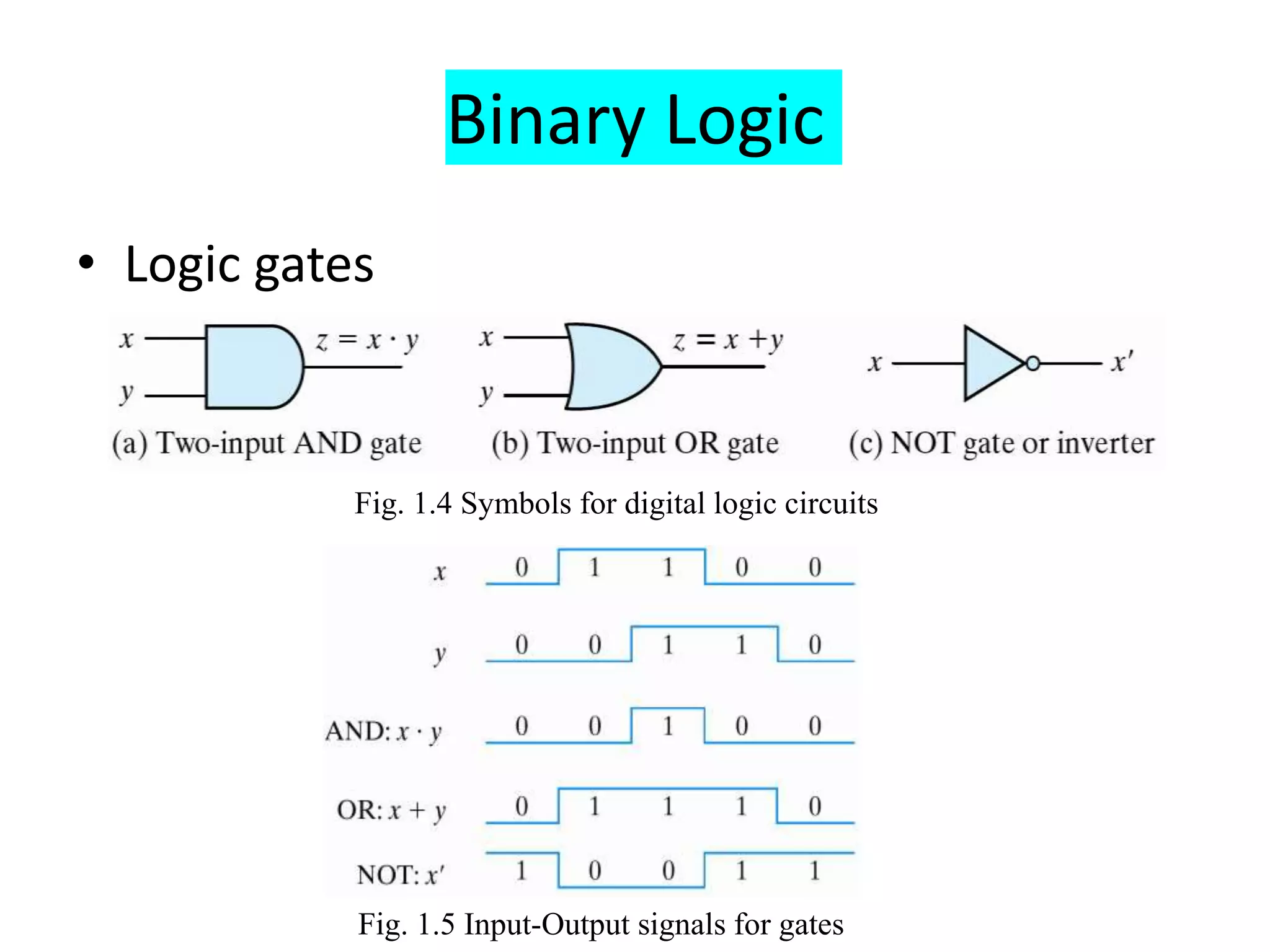
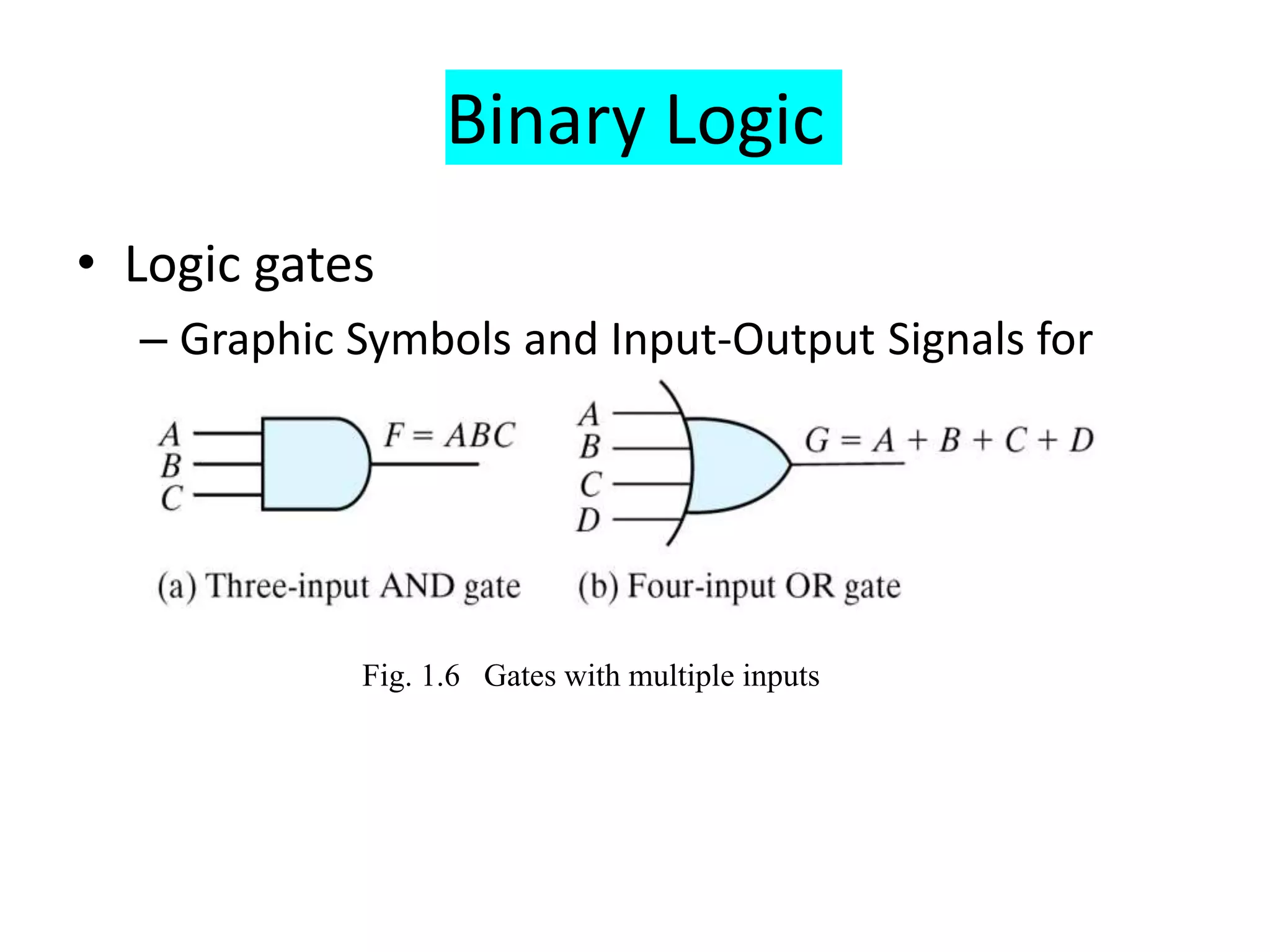
The document provides information about number systems used in computers. It discusses binary system which uses two digits (0 and 1) to represent ON and OFF states of switches in a computer. It explains how to convert between binary, decimal, octal and hexadecimal number systems using different methods. The document also covers signed binary numbers, binary codes like ASCII and Gray codes. Finally, it discusses binary logic, truth tables, Boolean expressions and logic gates used in switching circuits.

1. UNIT – I
Number Systems
P Suresh Babu,
VNRVJIET

2. 2
Why Binary System?
• Computers are made of a series of switches
• Each switch has two states: ON or OFF
• Each state can be represented by a number – 1
for “ON” and 0 for “OFF”

3. 3
Converting Base-2 to Base-10
(1 0 1 1)
2
0
ON
OFF
ON
OFF
ON
Exponent:
Calculation: 0 0 2 1
16+ + + + =
(19)10

4. 4
• Number systems include Decimal, Binary,
Octal and Hexadecimal.
• Each system have four number base
Number System Base Symbol
Binary Base- 2 B
Octal Base- 8 O
Decimal Base- 10 D
Hexadecimal Base- 16 H

5. 5
1.Decimal Number System
• The Decimal Number System uses base 10. It
includes the digits {0, 1,2,…, 9}. The weighted
values for each position are:
10^4 10^3 10^2 10^1 10^0 10^-1 10^-2 10^-3
10000 1000 100 10 1 0.1 0.01 0.001
Base
Right of decimal point
left of the decimal point

6. 6
• Each digit appearing to the left of the decimal
point represents a value between zero and nine
times power of ten represented by its position in
the number.
• Digits appearing to the right of the decimal point
represent a value between zero and nine times an
increasing negative power of ten.
• Ex: the value 725.194 is represented in expansion
form as follows:
• 7 * 10^2 + 2 * 10^1 + 5 * 10^0 + 1 * 10^-1 + 9 *
10^-2 + 4 * 10^-3
• =7 * 100 + 2 * 10 + 5 * 1 + 1 * 0.1 + 9 * 0.01 + 4 *
0.001
• =700 + 20 + 5 + 0.1 + 0.09 + 0.004
• =725.194

7. 7
The Binary Number System
• Most modern computer system using binary logic. The
computer represents values(0,1) using two voltage levels
(usually 0V for logic 0 and either +3.3 V or +5V for logic
1).
• The Binary Number System uses base 2 includes only the
digits 0 and 1
• The weighted values for each position are :
2^5 2^4 2^3 2^2 2^1 2^0 2^-1 2^-2
32 16 8 4 2 1 0.5 0.25
Base

8. 8
1.3 Number Base Conversion
• Binary to Decimal: Multiply each digit by its
weighted position, and add each of the weighted
values together or use expansion formdirectly.
Ex: The binary value 1100 1010 represents :
• 1*2^7 + 1*2^6 + 0*2^5 + 0*2^4 + 1*2^3 + 0*2^2 +
1*2^1 + 0*2^0 =
• 1 * 128 + 1 * 64 + 0 * 32 + 0 * 16 + 1 * 8 + 0 * 4 + 1 *
2 + 0 * 1 =
• 128 + 64 + 0 + 0 + 8 + 0 + 2 + 0 =202

9. 9
• Decimal to Binary
There are two methods, that may be used to convert
from integer number in decimal form to binary form:
I. Repeated Division By 2
• For this method, divide the decimal number by 2,
• If the remainder is 0, on the right side write down a 0.
• If the remainder is 1, write down a 1.
• When performing the division, the remainders which
will represent the binary equivalent of the decimal
number are written beginning at the least significant
digit (right) and each new digit is written to more
significant digit (the left) of the previous digit.

10. 10
• Example: convert the number 333 to binary.
Division Quotient Remainder Binary
333/2 166 1 1
166/2 83 0 01
83/2 41 1 101
41/2 20 1 1101
20/2 10 0 01101
10/2 5 0 001101
5/2 2 1 1001101
2/2 1 0 01001101
1/2 0 1 101001101

11. 11
Octal Number System
• Computer scientists are often looking for
shortcuts to do things
• One of the ways in which we can represent
binary numbers is to use their octal
equivalents instead
• This is especially helpful when we have to do
fairly complicated tasks using numbers

12. 12
• The octal numbering system includes eight base digits
(0-7)
• After 7, the next placeholder to the right begins with
a “1”
• 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13 ...

13. 13
Decimal to Octal: Transform (44978)10 to Octal
• .
Division Quotient Remainder Binary
44978 / 8 5622 2 2
5622 / 8 702 6 62
702/8 87 6 662
87/8 10 7 7662
10/8 1 2 27662
1/8 0 1 127662

14. 14
Exercise
• Fill in the blanks.
Decimal Binary Hexadecimal Octal
1101.0112
10101.112
245.62510
70310
A8516

15. 15
•Answers
Decimal Binary Hexadecimal Octal
13.37510 1101.0112 D.616 15.38
21.7510 10101.112 15.C16 25.68
245.62510 11110101.1012 F5.A16 365.58
70310 10101111112 2BF16 12778
269310 1010100001012 A8516 52058

16. • SIGNED BINARY NUMBERS
• BINARY CODES
• BINARY LOGIC

17. Binary Addition
• Column Addition
1 0 1
1
1
1
1
1
1
1 0
+
0
0
0
0 1 1
1
≥ (2)10
1
1
1
1
1
1
= 61
= 23
= 84

18. Binary Subtraction
• Borrow a “Base” when needed
0 0 1
1
1
0
1
1
1
1 0
−
0
1
0
1 1 1
0
= (10)2
2
2
2 2
1
0
0
0
1
= 77
= 23
= 54

19. Binary Multiplication
• Bit by bit
0
1 1 1 1
0
1 1 0
0
0 0 0 0
0
1 1 1 1
0
1 1 1 1
0 0 0
0
0
0
1
1
0
1
1
1 0
x

20. Complements
• There are two types of complements for each base-r system: the radix complement
and diminished radix complement.
• Diminished Radix Complement - (r-1)’s Complement
– Given a number N in base r having n digits, the (r–
1)’s complement of N is defined as:
(rn –1) – N
• Example for 6-digit decimal numbers:
– 9’s complement is (rn – 1)–N = (106–1)–N = 999999–
N
– 9’s complement of 546700 is 999999–546700 =
453299
• Example for 7-digit binary numbers:
– 1’s complement is (rn – 1) – N = (27–1)–N =

21. Complements
• 1’s Complement (Diminished Radix
Complement)
– All ‘0’s become ‘1’s
– All ‘1’s become ‘0’s
Example (10110000)2
 (01001111)2
If you add a number and its 1’s complement …
1 0 1 1 0 0 0 0
+ 0 1 0 0 1 1 1 1
1 1 1 1 1 1 1 1

22. Signed Binary Numbers
• To represent negative integers, we need a
notation for negative values.
• It is customary to represent the sign with a bit
placed in the leftmost position of the number
since binary digits.
• The convention is to make the sign bit 0 for
positive and 1 for negative.
• Example:

23. Signed Binary Numbers
• Arithmetic addition
– The addition of two numbers in the signed-magnitude system follows the rules
of ordinary arithmetic. If the signs are the same, we add the two magnitudes
and give the sum the common sign. If the signs are different, we subtract the
smaller magnitude from the larger and give the difference the sign if the larger
magnitude.
– The addition of two signed binary numbers with negative numbers
represented in signed-2's-complement form is obtained from the addition of
the two numbers, including their sign bits.
– A carry out of the sign-bit position is discarded.
• Example:

24. Signed Binary Numbers
• Arithmetic Subtraction
– In 2’s-complement form:
• Example:
1. Take the 2’s complement of the subtrahend (including the sign bit)
and add it to the minuend (including sign bit).
2. A carry out of sign-bit position is discarded.
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
A B A B
A B A B
      
      
( 6)  ( 13) (11111010  11110011)
(11111010 + 00001101)
00000111 (+ 7)

25. Binary Codes
• BCD Code
– A number with k decimal
digits will require 4k bits in
BCD.
– Decimal 396 is
represented in BCD with
12bits as 0011 1001 0110,
with each group of 4 bits
representing one decimal
digit.
– A decimal number in BCD
is the same as its

26. Binary Codes
• Example:
– Consider decimal 185 and its corresponding value
in BCD and binary:
• BCD addition

27. Binary Codes
• Gray Code
– The advantage is that
only bit in the code
group changes in going
from one number to the
next.
• Error detection.
• Representation of analog data.
• Low power design.
000 001
010
100
110 111
101
011
1-1 and onto!!

28. Binary Codes
• ASCII Character Code

29. ASCII Character Codes
• American Standard Code for Information Interchange
(Refer to Table 1.7)
• A popular code used to represent information sent as
character-based data.
• It uses 7-bits to represent:
– 94 Graphic printing characters.
– 34 Non-printing characters.
• Some non-printing characters are used for text
format (e.g. BS = Backspace, CR = carriage return).
• Other non-printing characters are used for record
marking and flow control (e.g. STX and ETX start and
end text areas).

30. ASCII Properties
• ASCII has some interesting properties:
– Digits 0 to 9 span Hexadecimal values 3016 to 3916
– Upper case A-Z span 4116 to 5A16
– Lower case a-z span 6116 to 7A16
• Lower to upper case translation (and vice versa) occurs by flipping bit 6.

31. Binary Logic
• Definition of Binary Logic
– Binary logic consists of binary variables and a set of logical operations.
– The variables are designated by letters of the alphabet, such as A, B, C, x, y, z,
etc, with each variable having two and only two distinct possible values: 1 and
0,
– Three basic logical operations: AND, OR, and NOT.

32. Binary Logic
• Truth Tables:
x y z
0 0 0
0 1 0
1 0 0
1 1 1
x y z
0 0 0
0 1 1
1 0 1
1 1 1
x z
0 1
1 0
AND OR NOT
x
y z x
y z
z = x • y = x y z = x + y z = x = x’
x z
• Boolean
Expressions:
• Logic Gates:

33. Switching Circuits
AND OR

34. Binary Logic
• Logic gates
– Graphic Symbols and Input-Output Signals for
Logic gates:
Fig. 1.4 Symbols for digital logic circuits
Fig. 1.5 Input-Output signals for gates

35. Binary Logic
• Logic gates
– Graphic Symbols and Input-Output Signals for
Logic gates:
Fig. 1.6 Gates with multiple inputs