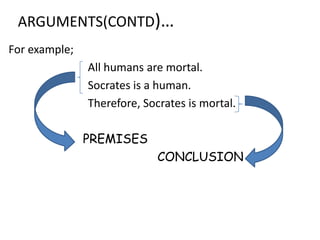
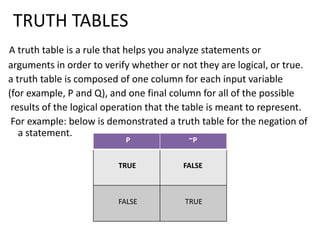
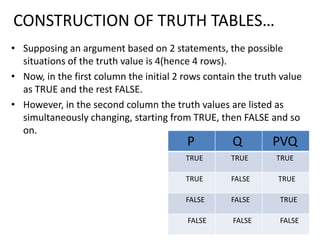
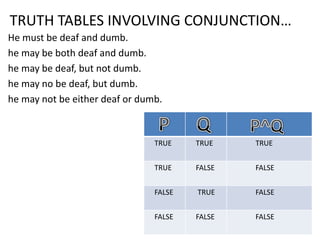
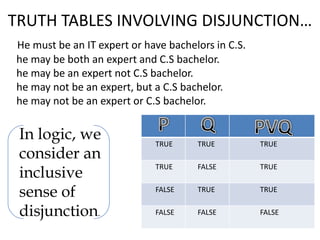
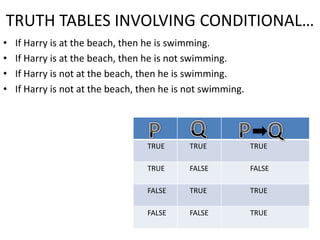
This document provides an overview of logic and arguments. It discusses the components of arguments, including premises and conclusions. It also discusses the validity and invalidity of arguments, which can be determined using truth tables. The document goes on to explain how to construct truth tables based on the number of statements, and provides examples of truth tables involving conjunction, disjunction, and conditionals. It concludes by summarizing when arguments are considered true for different logical connectives.

2. MAIN TOPICS TO BE COVERED…
• OVERVIEW
( INCLUDED ARE ARGUMENTS & THEIR VALIDITY AND INVALIDITY )
• TRUTH TABLES???
• CONSTRUCTING A TRUTH TABLE
• VARIOUS FORM OF TRUTH TABLES
• CONCLUSION
• QUESTION/ANSWER SESSION

3. ARGUMENTS
In logic and philosophy, an is an attempt to persuade
someone of something, by giving reasons for accepting a
particular conclusion as evident.
An argument can also be defined as a set of statements, of which
one is being supported by others.
The statement being supported is called .
And the statements which support are called .

4. ARGUMENTS(CONTD)…
For example;
All humans are mortal.
Socrates is a human.
Therefore, Socrates is mortal.
PREMISES
CONCLUSION

5. VALIDITY AND INVALIDITY OF ARGUMENTS…
Arguments can be either valid or invalid,
depending upon whether the premises lead to a
reasonable conclusion or not.
In case if the premises lead to a reasonable
conclusion, the argument can be termed as valid.
On the contrary, if the premises fail to lead to a
reasonable conclusion, the argument can be termed
as invalid.
Whether an argument is valid or not can be
determined with the help of truth tables…

6. VALIDITY AND INVALIDITY OF ARGUMENTS…
Here is given an example of an invalid argument;
All humans are mortals.
Socrates is a mortal.
Therefore Socrates is a human.
The premises, in the given argument, do not lead to the
conclusion as not necessarily all the mortals are humans.
In fact every being is subject to mortality. For Socrates
being mortal does not lead to the conclusion that he
must be human. He can be a different entity too.

7. TRUTH TABLES
A truth table is a rule that helps you analyze statements or
arguments in order to verify whether or not they are logical, or true.
a truth table is composed of one column for each input variable
(for example, P and Q), and one final column for all of the possible
results of the logical operation that the table is meant to represent.
For example: below is demonstrated a truth table for the negation of
a statement.
TRUE FALSE
FALSE TRUE
P ~P

8. CONSTRUCTION OF TRUTH TABLES…
• According to the principle of bi-valence the truth value of every
statement is either ‘true’ or ‘false’ and in every situation a
statement has only one of it.
• the number of rows in a truth table is determined by the
formula 2n
• ‘n’ equals the number of statements on which the argument
operates(for ‘n’ equaling 2, the number of rows is 4).
• Statements are denoted by sentence letters and each sentence
letter heads a column in which the possible truth values of that
statement are mentioned.

9. CONSTRUCTION OF TRUTH TABLES…
• Supposing an argument based on 2 statements, the possible
situations of the truth value is 4(hence 4 rows).
• Now, in the first column the initial 2 rows contain the truth value
as TRUE and the rest FALSE.
• However, in the second column the truth values are listed as
simultaneously changing, starting from TRUE, then FALSE and so
on.
TRUE TRUE TRUE
TRUE FALSE TRUE
FALSE FALSE TRUE
FALSE FALSE FALSE
P Q PVQ

10. TRUTH TABLES INVOLVING CONJUNCTION…
He must be deaf and dumb.
he may be both deaf and dumb.
he may be deaf, but not dumb.
he may no be deaf, but dumb.
he may not be either deaf or dumb.
TRUE TRUE
TRUE FALSE
FALSE TRUE
FALSE FALSE
TRUE
FALSE
FALSE
FALSE

11. TRUTH TABLES INVOLVING DISJUNCTION…
He must be an IT expert or have bachelors in C.S.
he may be both an expert and C.S bachelor.
he may be an expert not C.S bachelor.
he may not be an expert, but a C.S bachelor.
he may not be an expert or C.S bachelor.
TRUE TRUE
TRUE FALSE
FALSE TRUE
FALSE FALSE
TRUE
TRUE
TRUE
FALSE
In logic, we
consider an
inclusive
sense of
disjunction.

12. TRUTH TABLES INVOLVING CONDITIONAL…
• If Harry is at the beach, then he is swimming.
• If Harry is at the beach, then he is not swimming.
• If Harry is not at the beach, then he is swimming.
• If Harry is not at the beach, then he is not swimming.
TRUE TRUE
TRUE FALSE
FALSE TRUE
FALSE FALSE
TRUE
FALSE
TRUE
TRUE

13. CONCLUSION…
• Arguments involving conjunction are true only if both the statements
are true.
• Arguments involving disjunction are true if both the premises are
true and if one statement is true.
• Arguments involving conditional are true if both the statements are
true or only a single statement is true.

14. QUESTION AND ANSWER SESSION…???