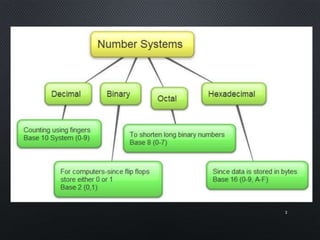
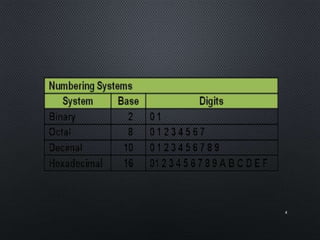
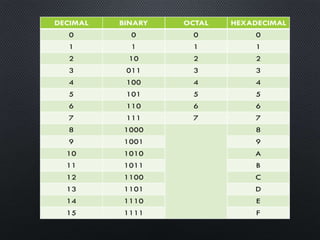
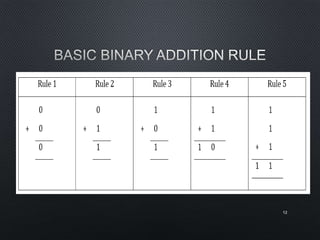
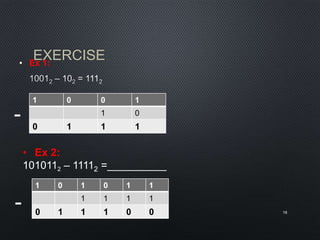
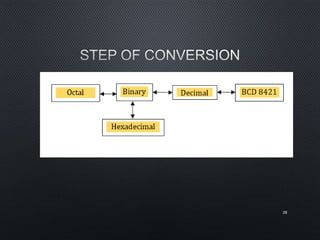
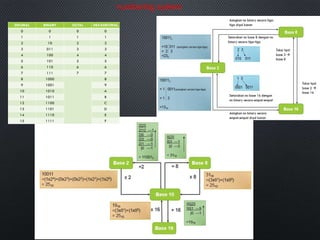
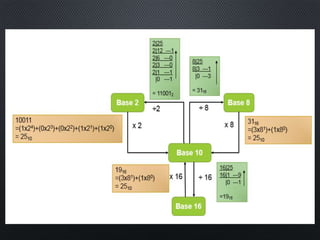
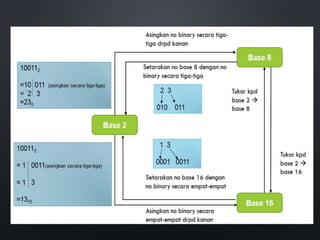
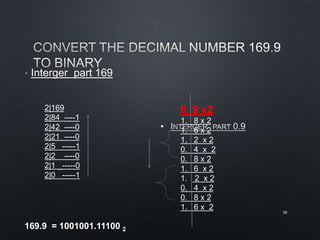
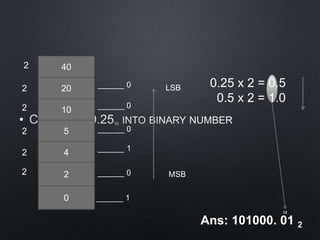
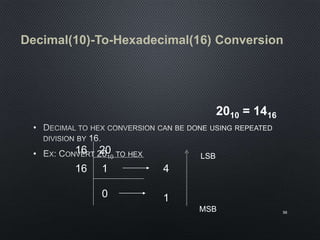
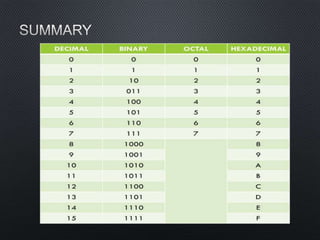
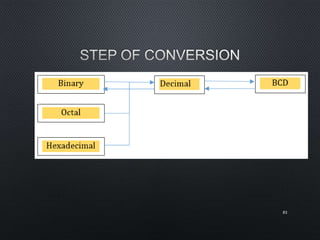
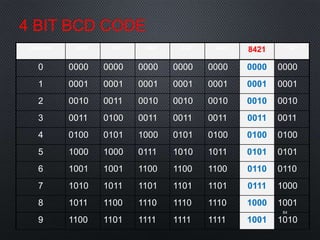
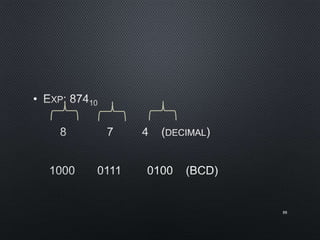
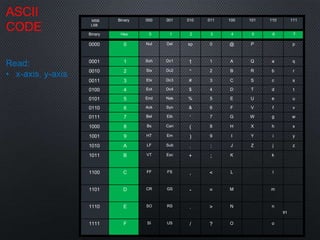
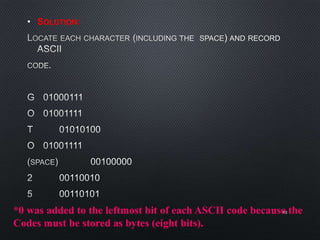
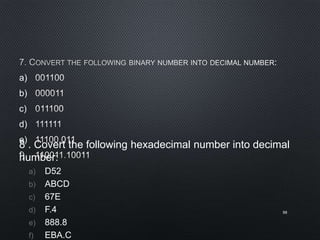
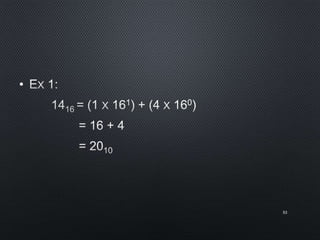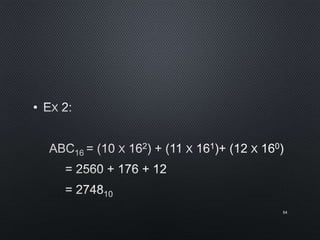This document discusses data representation on a CPU, including numbering systems such as decimal, binary, octal, and hexadecimal. It covers converting between these numbering systems, binary arithmetic, ones' complement, twos' complement, signed numbers, coding systems such as ASCII, and digital logic components. The document provides examples of performing arithmetic in different numbering systems and converting between binary, decimal, octal, and hexadecimal.

1. 2.1 DATA REPRESENTATION
ON CPU
1
SUMMARY: This topic introduces the numbering systems: decimal, binary, octal
and hexadecimal. The topic covers the conversion between numbering systems,
binary arithmetic, one's complement, two's complement, signed number and
coding system. This topic also covers the digital logic components.
CLO 2:apply appropriate method to solve arithmetic problem in numbering
system (C3).

2. 1.
2.
3.
4.
a)
b)
c)
d)
2

3. 3

4. 4

5. 5

6. INTRODUCTION
•
•
•
•
6

7. DECIMAL NUMBERING SYSTEM(10 DIGIT)
• 10
7
 These 10 sysmbols are 0, 1, 2, 3, 4, 5, 6,
7, 8, 9.
 Using these symbols as digits of a number,
it can express any quantity.

8. •
•
8
23410
Basic number
Base number
DECIMAL NUMBERING SYSTEM(10 DIGIT)

9. ADDITION DECIMAL NUMBERS

9
L1 = 7 + 5 =12 – 10 = 2
L2 = 5 + 4 = 9 + 1 -10 = 0
L3 = 4 + 2 = 6 + 1 = 7

10. SUBTRACTION DECIMAL NUMBERS
•
10
L1 = 7 - 5 = 2
L2 = 5 +10 – 6 =9
L3 = 3 – 2 = 1

11. BINARY NUMBERING SYSTEM (2 DIGIT)
•
•
11
10112
Basic number
Base number
Define Binary numbers
-Binary numbers representing number in which only digits 0 or 1.

12. 12

13. •
13

14. EXERCISE
• EX 1:
14
1 0 1 1 1
1 1 1
1 1 1 1 0
+
1 1 0 1 1
1 0 0 0 1
10 1 1 0 0
+
Ex 2:
101112 + 1112 = ________

15. SUBTRACTION
15

16. EXERCISE• EX 1:
16
1 0 0 1
1 0
0 1 1 1
-
• Ex 2:
1010112 – 11112 =__________
1 0 1 0 1 1
1 1 1 1
0 1 1 1 0 0
-

17. OCTAL NUMBERING SYSTEM ( 8 DIGIT )
•
•
17
2568
Basic number
Base number

18. 18

19. OCTAL NUMBER - ADDITION
•
19
4448
 Ex:
4578
+ 2458

20. OCTAL NUMBER - (SUBTRACTION)
•
20
 Ex:
5248
- 1678
 Ex:
1678
- 248

21. HEXADECIMAL NUMBERING SYSTEM
( 16 DIGIT )
•
•
•
21
7A16
Basic number
Base number

22. HEXADECIMAL NUMBER -
ADDITION
•
22
 Ex:
2 0 D 316
+ 1 2 B C16
7 A16

23. HEXADECIMAL NUMBER -
SUBTRACTION
23
 Ex:
4 416
- 1 716
 Ex:
3 2 5 516
- 3 1 8 216
2 D16

24. 1.
a)
b)
c)
d)
e)
f)
g)
h)
i) 24

25. 25

26. FORMULA CONVERTING BETWEEN
NUMBER BASES2 TO10
10 TO 2:
B) 2 TO 8:
8 TO 2:
C) 2 TO 16 :
16 TO 2: 26
  
5
101
4
100
1
001
 
9
1001
14
1110
 A
1010
3
0011

27. 8 TO10
10 TO 8
16 TO 10
10 TO 16
8 TO 16 8 TO 10 TO 16 8 TO 2 TO 16
16 TO 8 16 TO 2 TO 8 16 TO 10 TO 8
27

28. 28

29. numbering system

30. 30

31. 31

32. BINARY (2) TO DECIMAL (10)
CONVERSIONS
32
Conversions Between Base Number

33. BINARY (2) TO DECIMAL (10) CONVERSIONS

33

34. 34

35. 1.
2.
35
Ans: 31.25
Ans:29.75

36. •
36
• Interger part 169
2|169
2|84 ----1
2|42 ----0
2|21 ----0
2|5 -----1
2|2 ----0
2|1 _-----0
2|0 -----1
0. 9 x2
1. 8 x 2
1. 6 x 2
1. 2 x 2
0. 4 x 2
0. 8 x 2
1. 6 x 2
1. 2 x 2
0. 4 x 2
0. 8 x 2
1. 6 x 2
169.9 = 1001001.11100 2

37. 
37
25
12
2
2 ______ 1
6
3
1
2
2
______ 0
______ 0
______ 1
2
0 ______ 1 MSB
LSB
2510 = 110012
Decimal (10) to Binary (2) conversions

38. •
38
40
20
2
2 ______ 0
10
5
4
2
2
______ 0
______ 0
______ 1
2
2 ______ 0 MSB
LSB
0
2
______ 1
0.25 x 2 = 0.5
0.5 x 2 = 1.0
Ans: 101000. 01 2

39. 1. CONVERT 3010 INTO BINARY NUMBER
2. CONVERT 51.1210 INTO BINARY NUMBER
39
Ans: 111102
Ans:110011.00012

40. OCTAL (8) –TO-DECIMAL(10)
CONVERSION
•
•
40
84 83 82 81 80 •. 8-1 8-2 8-3
=
1
81
=
1
82
=
1
83

41. OCTAL (8) –TO-DECIMAL(10) CONVERSION
•
41

42. •
42

43. •
•
43
Ans: 41210
Ans: 213.7810

44. DECIMAL(10)-TO-OCTAL(8) CONVERSION
•
44
891
111
8
8 ______ 3
13
1
0
8
8
______ 7
______ 5
______ 1
LSB
MSB
• Convert 891 10 into octal number
Ans: 1573 8

45. •
45
• Interger part 169
8|169
8|21 ----1
8|2 -----5
|0 -----2
0. 9 x8
7. 2 x 8
1. 6 x 8
4. 8 x 8
6. 4 x 8
3. 2 x 8
1. 6 x 8
4 . 8 x 8
6. 4 x 8
3. 2 x 8
1. 6 x 8
169.9 = 251.71463 8

46. •
•
46
Ans: 6348
Ans: 325.6178

47. OCTAL(8) –TO- BINARY (2)
CONVERSION
47

48. BINARY(2) TO OCTAL
(8)CONVERSION
48

49. • CONVERT INTO BINARY NUMBER
• CONVERT INTO BINARY NUMBER
49
Ans: 1111011110102
Ans: 1011001102

50. • CONVERT 1010111112 INTO OCTAL NUMBER
• CONVERT INTO OCTAL NUMBER
50
Ans: 5378
Ans: 67308

51. HEXADECIMAL(16)-TO-DECIMAL(10)
CONVERSION
•
51

52. 52
= (2x16x16)+(14x16)+(6)+(10/16)+(3/(16x16))
= 512+ 224+6+0.625+ 0.0117
= 742.6367

53. •
53

54. •
54

55. • CONVERT INTO DECIMAL NUMBER
• CONVERT 138.C7AE16 INTO DECIMAL NUMBER
55
Ans: 312.7810
Ans: 3710

56. •
•
56
Decimal(10)-To-Hexadecimal(16) Conversion
16 20
16 1 4
2010 = 1416
0 1
LSB
MSB

57. •
57
• Interger part 169
16|169
16|10 --- 9
0 ---10--A
0. 9 x16
14. 4 x 16
6. 4 x 16
6. 4 x 16
169.9 = A9.E6 8
E

58. • CONVERT INTO HEX NUMBER
• CONVERT 125.2510 INTO HEX NUMBER
58
Ans: 7D.416
Ans: 1916

59. HEXADECIMAL (16)-TO-BINARY(2)
CONVERSION
•
•
•
59

60. •
60
9
1001
F
1111
2
0010
9F2 16 = 1001111100102

61. •
61
A
1010
B
1011
F
1111
ABF.3 16 = 101010111111.00112
.3
.0011

62. BINARY(2)-TO-HEXADECIMAL(16)
CONVERSION
• FOUR
•
•
62

63. •
63

64. • CONVERT 4DA .5 INTO BINARY NUMBER
• CONVERT 87E INTO BINARY NUMBER
64
Ans: 010011011010.01012
Ans: 1000011111102

65. • CONVERT 111100001010.101011 INTO
HEX NUMBER
• CONVERT 010111001110 INTO HEX NUMBER
65
Ans: F0A.AC2
Ans: 5CE2

66. •
66

67. •
67
0. 96875 x16
15. 5 x 16
8. 0 x 16
0. 0 x 16
F
0.96875 = 0.F816

68. •
68
0.F816 = 0.96875
0 x161 + 15x16-1 + 8x16-2
= 0.9375 +0.03125

69. 69

70. 2.1.4 DESCRIBE THE CODING SYSTEM
70
a. Sign and magnitude
b. 1’s Complement and 2’s Complement
c. Binary Coded Decimal (BCD system)
d. ASCII and EBCDIC

71. A. SIGN AND MAGNITUDE
•
•
• 0
• 1
71

72. B. ONE’S COMPLEMENTS AND
TWO’S COMPLEMENTS
• ONE’S COMPLEMENTS
•
•
0 TO 1 1 TO A
0.
• NEGATIVE
•
72

73. HOW CAN WE REPRESENT THE NUMBER -510 IN 1'S COMPLEMENT USING 8 BIT.
73

74. a)
b)
74

75. 75

76. 1.
2.
3.
4.
76

77. •
•
77
Two’s complement = One’s Complement + 1

78. HOW CAN WE REPRESENT THE NUMBER -510 IN 2'S COMPLEMENT USING 8-
BITS
78

79. •
79

80. 1.
2.
3.
4.
5.
6.
80

81. 1.
i.
ii.
iii.
iv.
81
Ans: 01000110 ( 1st comp)
01000111(2nd comp)
Ans: 010000001 ( 1st comp)
010000010 (2nd comp)
Ans: 1110110110111010 ( 1st comp)
1110110110111011 (2nd comp)
Ans: 0010 ( 1st comp)
0011 (2nd comp)

82. C. BCD CODE
•
•
•
82

83. 83

84. 4 BIT BCD CODE
Desimal 5421 5311 4221 3321 2421 8421 7421
0 0000 0000 0000 0000 0000 0000 0000
1 0001 0001 0001 0001 0001 0001 0001
2 0010 0011 0010 0010 0010 0010 0010
3 0011 0100 0011 0011 0011 0011 0011
4 0100 0101 1000 0101 0100 0100 0100
5 1000 1000 0111 1010 1011 0101 0101
6 1001 1001 1100 1100 1100 0110 0110
7 1010 1011 1101 1101 1101 0111 1000
8 1011 1100 1110 1110 1110 1000 1001
9 1100 1101 1111 1111 1111 1001 1010
84

85. BINARY-CODED-DECIMAL CODE
•
• DECIMAL DIGIT CAN BE AS LARGE AS 9, FOUR
BITS ARE REQUIRED TO CODE EACH DIGIT (THE
BINARY CODE FOR 9 IS 1001)
85

86. •
86

87. BCD 8421 CODE – TO –
BINARY NUMBER•
STEP 1
STEP 2
87

88. BINARY NUMBER – TO – BCD
8421 CODE•
STEP 1
STEP 2
88

89. 1.
a)
b)
c)
d)
e)
f)
89

90. •
•
•
90
d. ASCII Code

91. MSB
LSB
Binary 000 001 010 011 100 101 110 111
Binary Hex 0 1 2 3 4 5 6 7
0000 0 Nul Del sp 0 @ P p
0001 1 Soh Dc1 1 1 A Q a q
0010 2 Stx Dc2 “ 2 B R b r
0011 3 Etx Dc3 # 3 C S c s
0100 4 Eot Dc4 $ 4 D T d t
0101 5 End Nak % 5 E U e u
0110 6 Ack Syn & 6 F V f v
0111 7 Bel Etb ‘ 7 G W g w
1000 8 Bs Can ( 8 H X h x
1001 9 HT Em ) 9 I Y i y
1010 A LF Sub . : J Z j z
1011 B VT Esc + ; K k
1100 C FF FS , < L l
1101 D CR GS - = M m
1110 E SO RS . > N n
1111 F SI US / ? O o
ASCII
CODE
91
Read:
• x-axis. y-axis

92. GOTO 25
92

93. • SOLUTION:
93*0 was added to the leftmost bit of each ASCII code because the
Codes must be stored as bytes (eight bits).

94. 94

95. HOW THE CHARACTER SENT FROM
THE KEYBOARD TO THE
COMPUTER?
• STEP 1
• STEP 2
• STEP 3
• STEP 4 95

96. 1.
2.
3.
4.
5.
a)
b)
c)
d)
e) 96

97. a)
b)
c)
d)
e)
97

98. a)
b)
c)
d)
e)
f)
98
8 . Covert the following hexadecimal number into decimal
number:
a) D52
b) ABCD
c) 67E
d) F.4
e) 888.8
f) EBA.C

99. a)
b)
c)
a)
b)
c)
99

100. a)
b)
c)
a)
b)
c)
d)
e)
100

101. a)
b)
c)
d)
e)
101