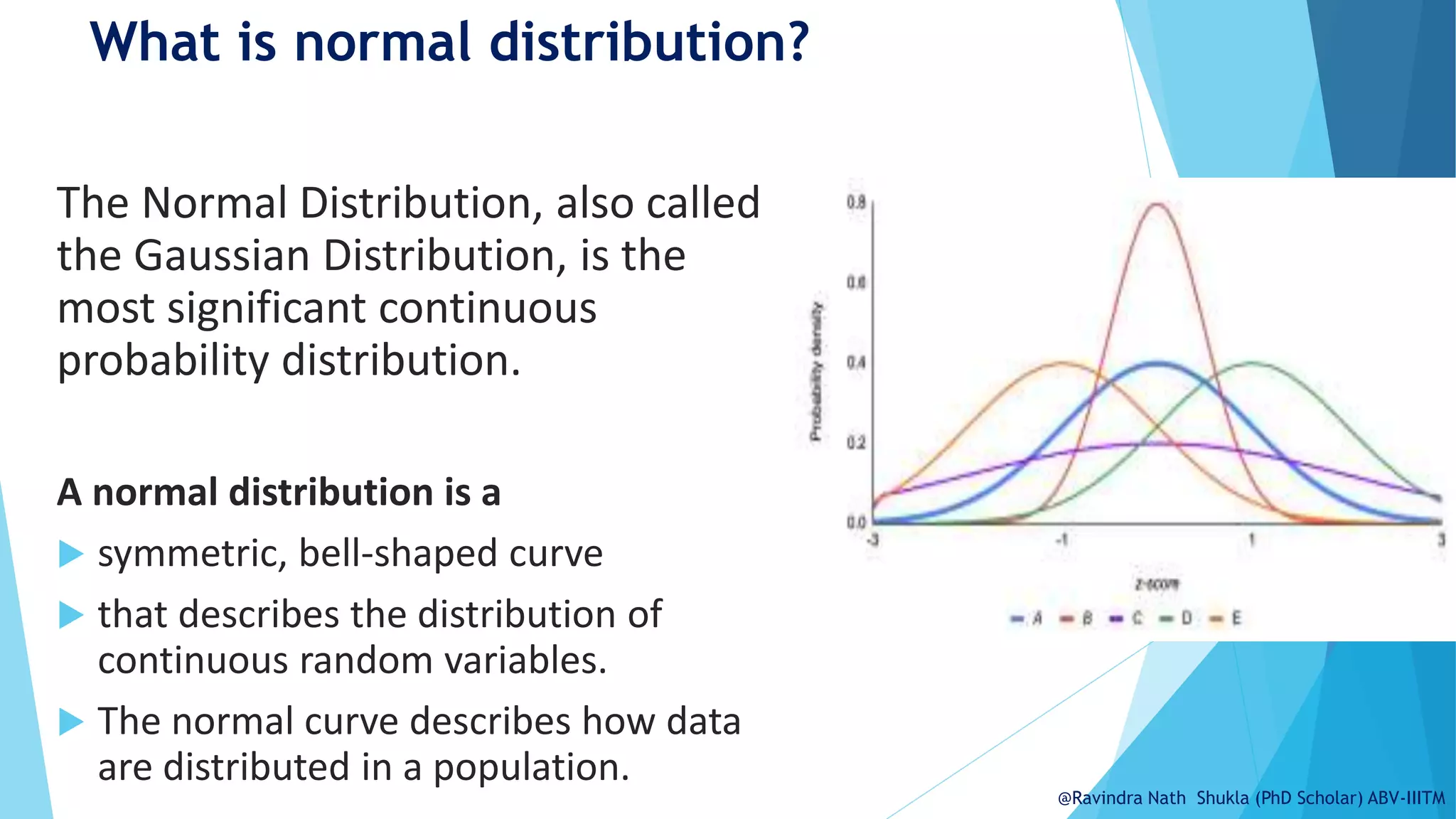
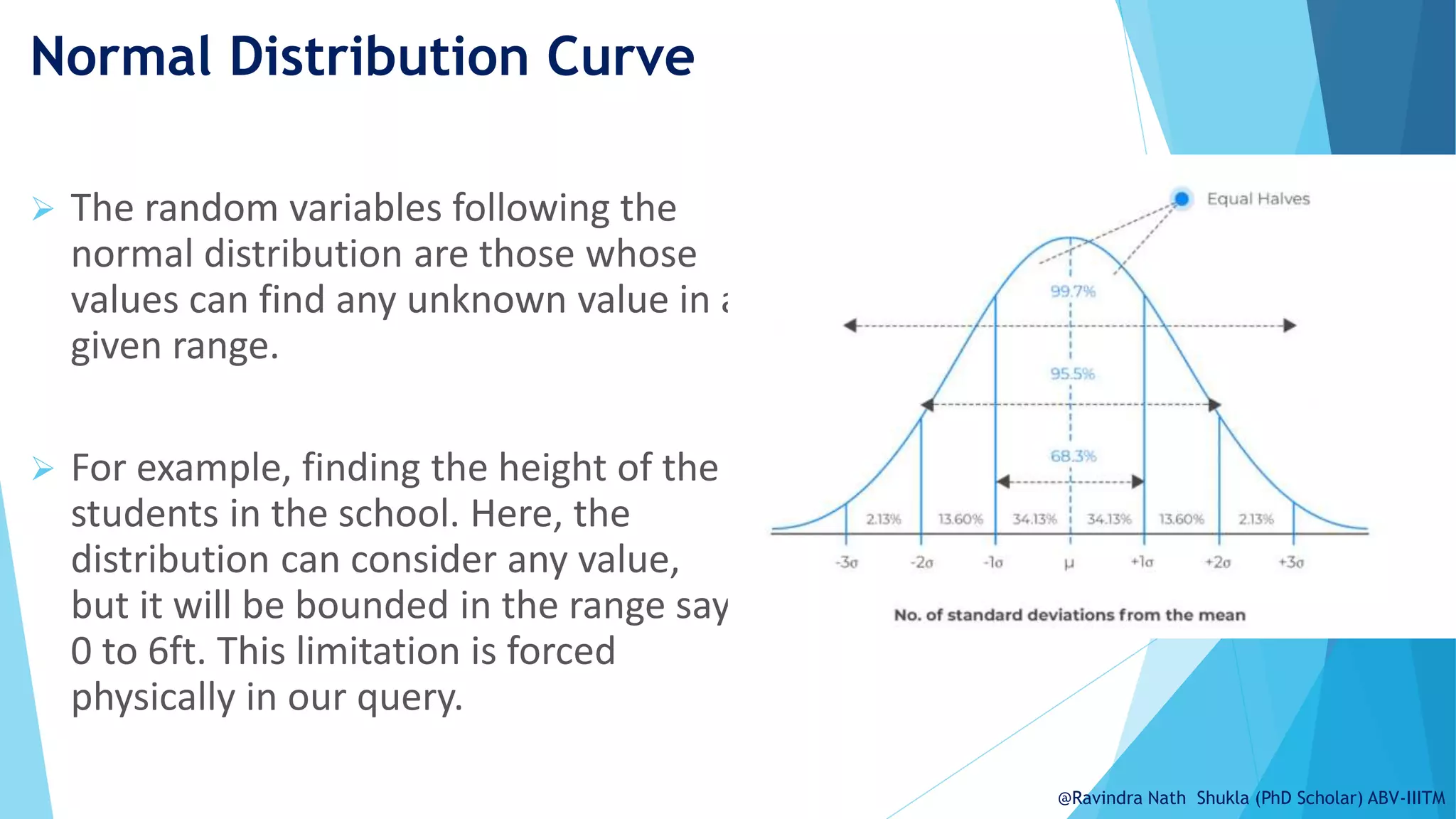
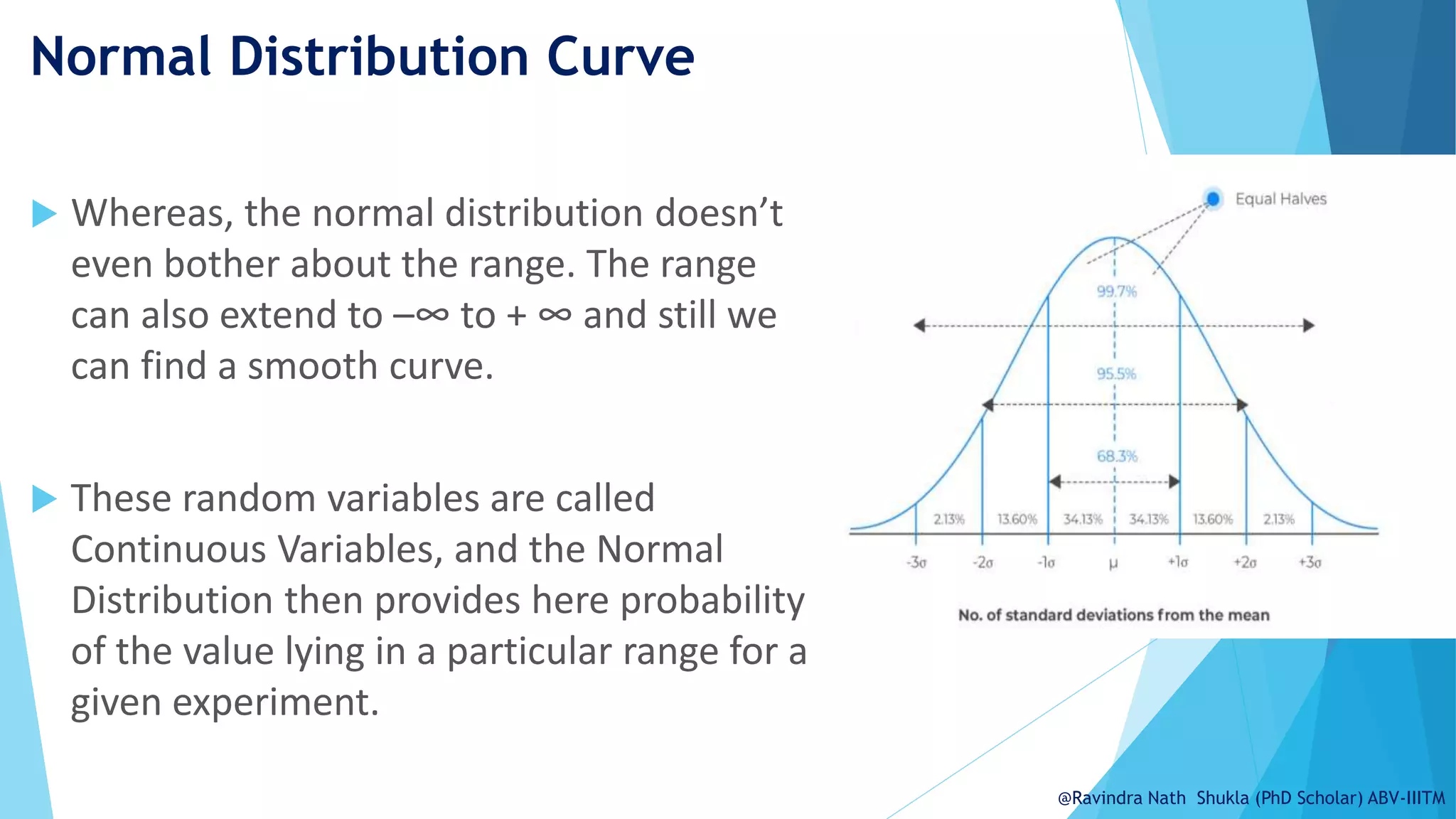
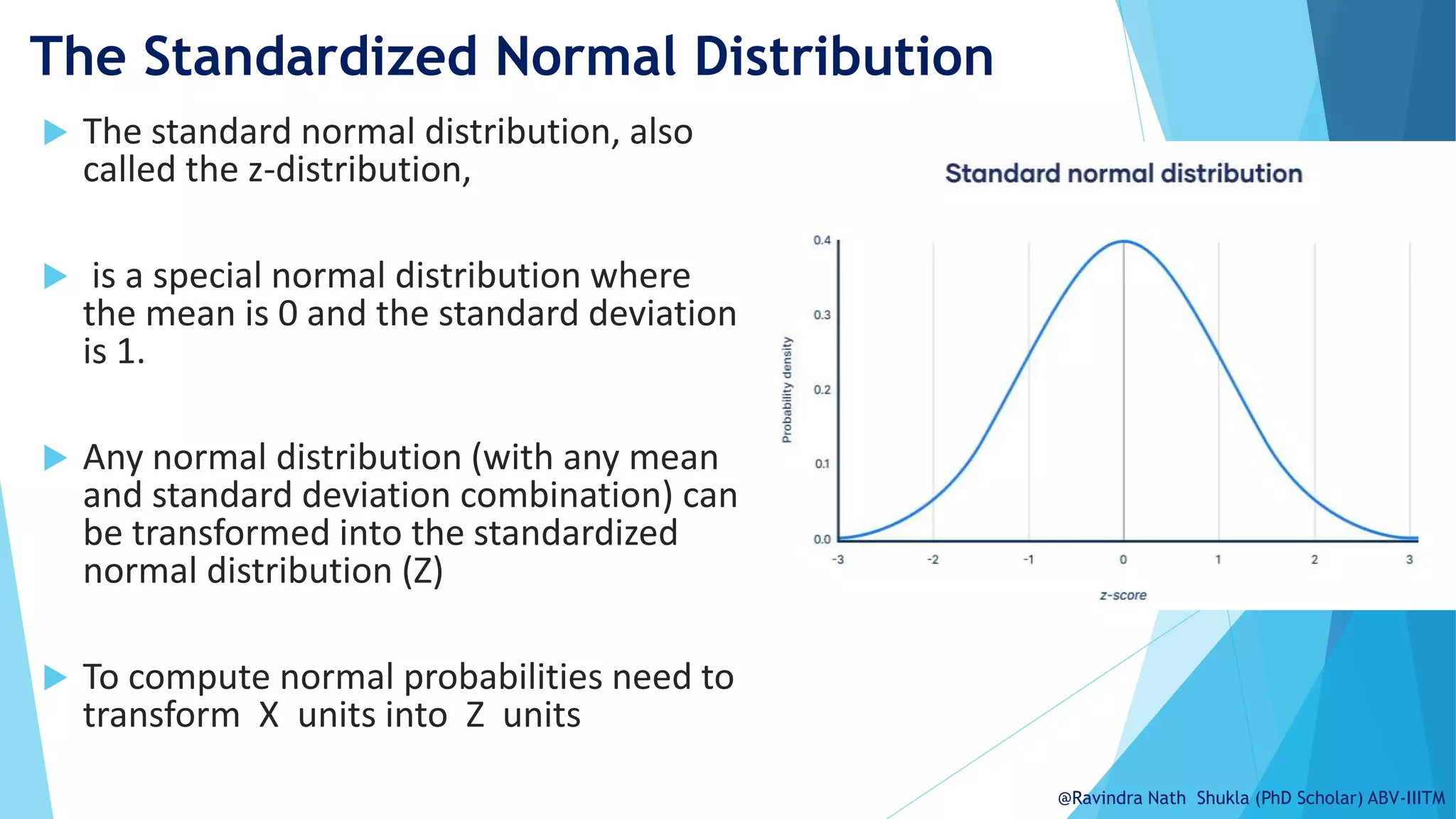
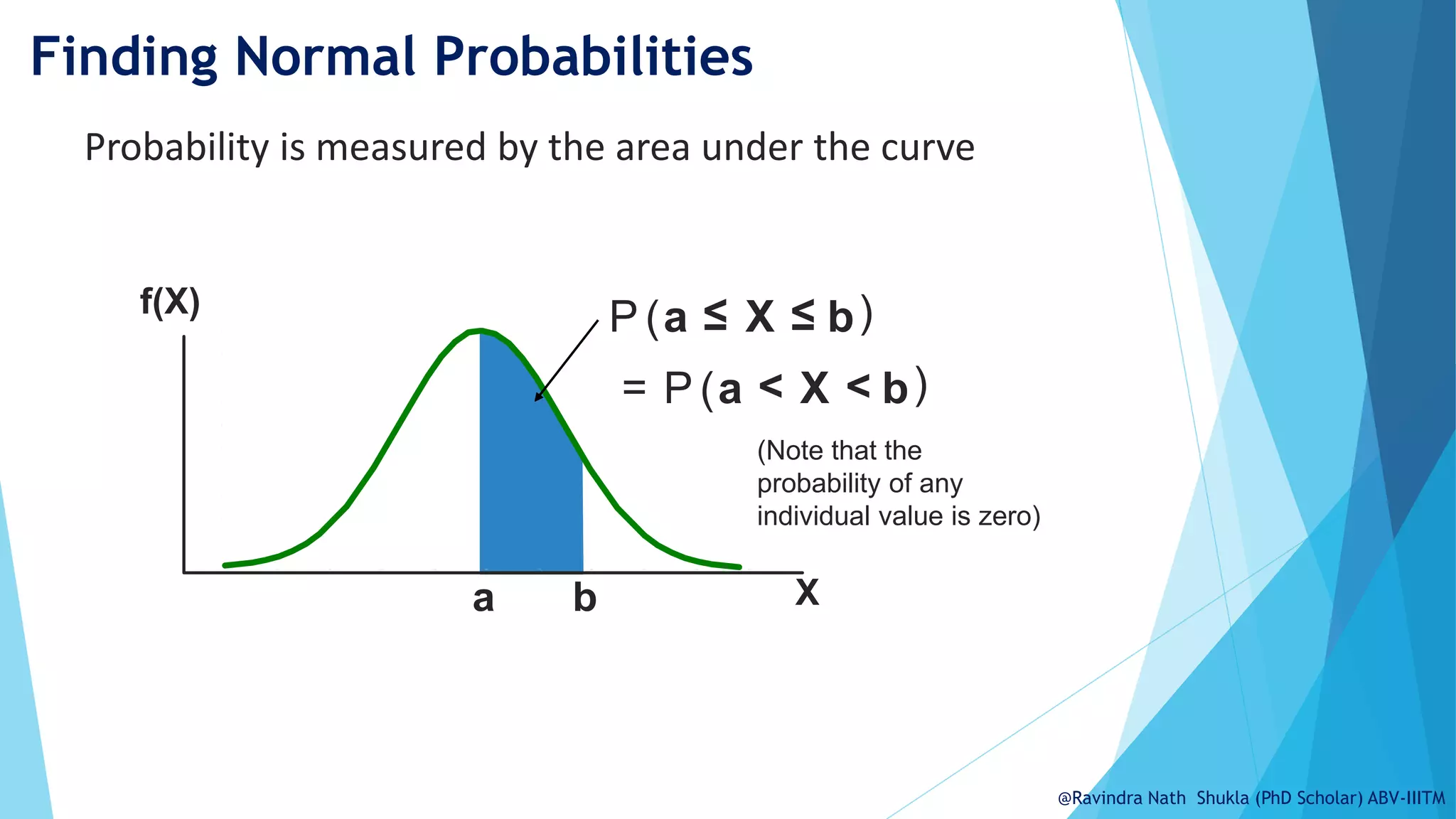
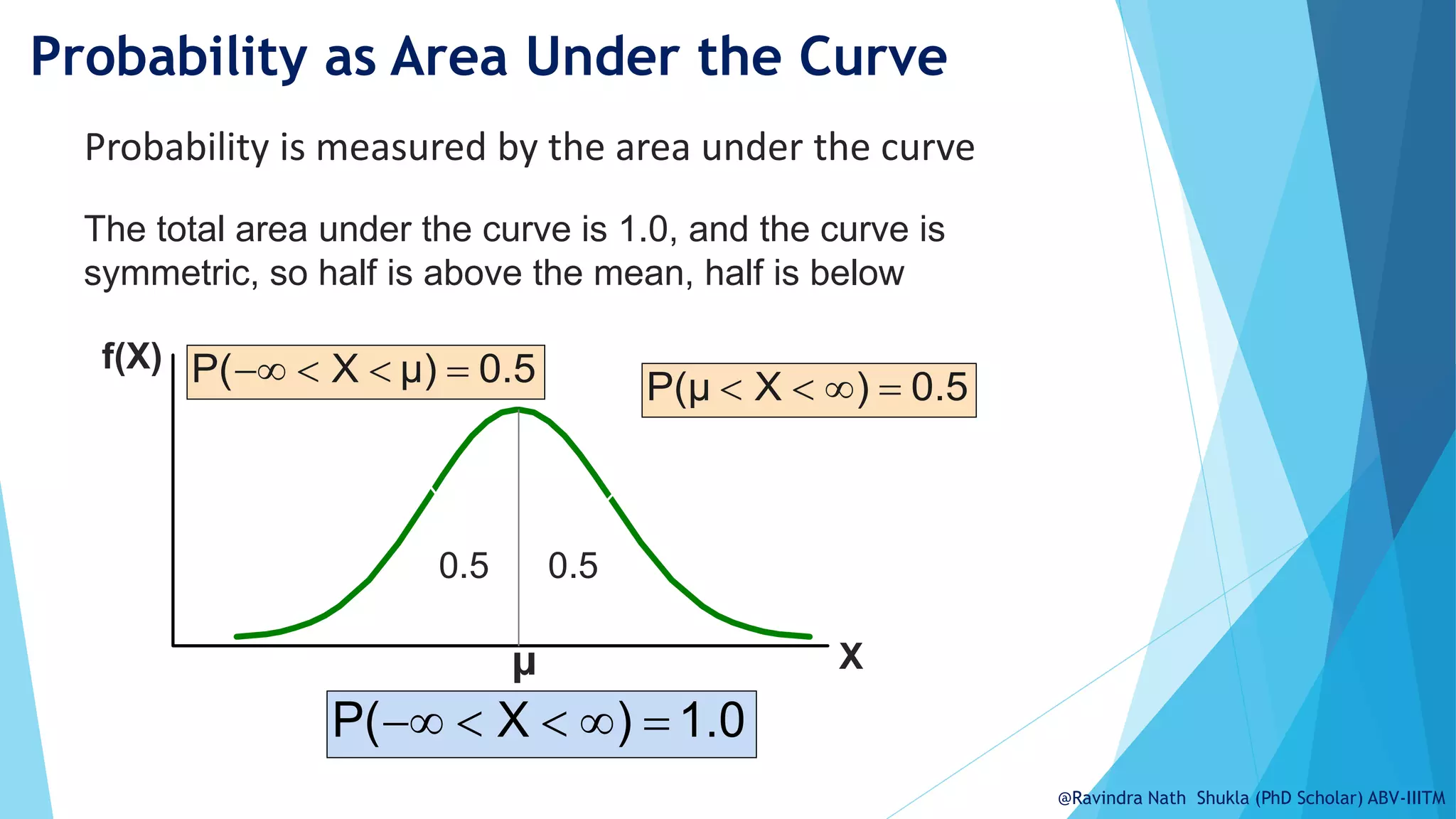
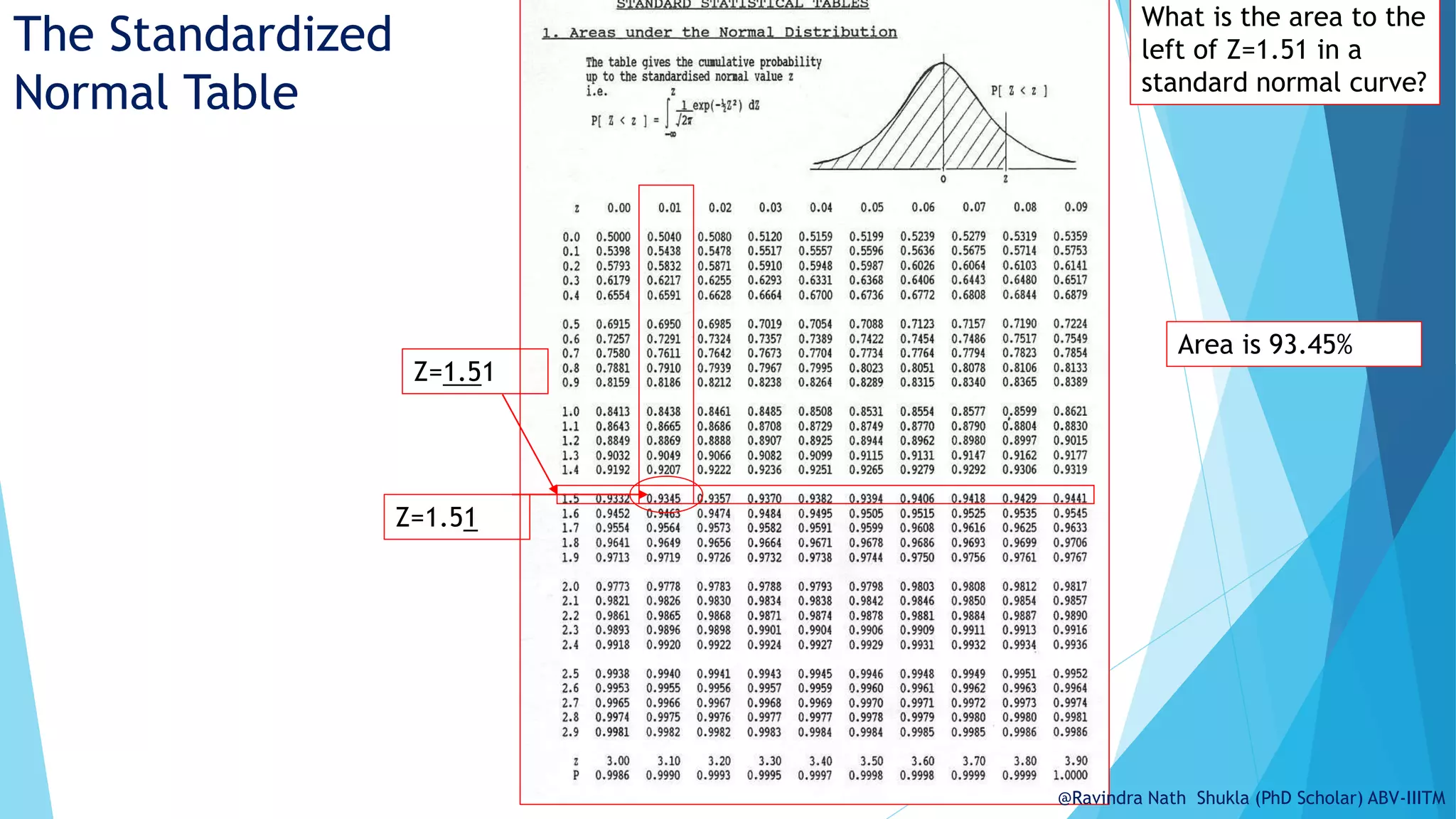
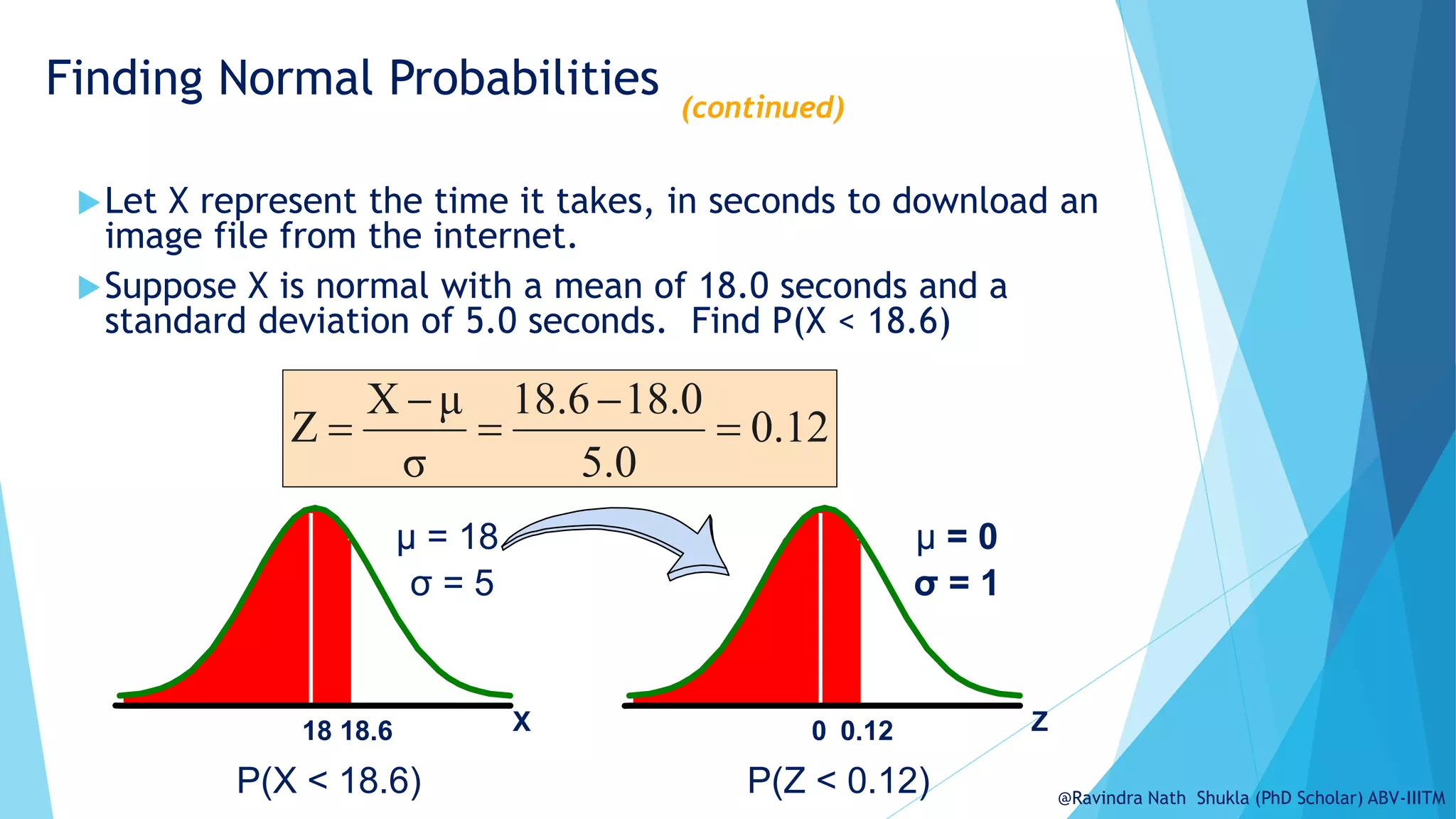
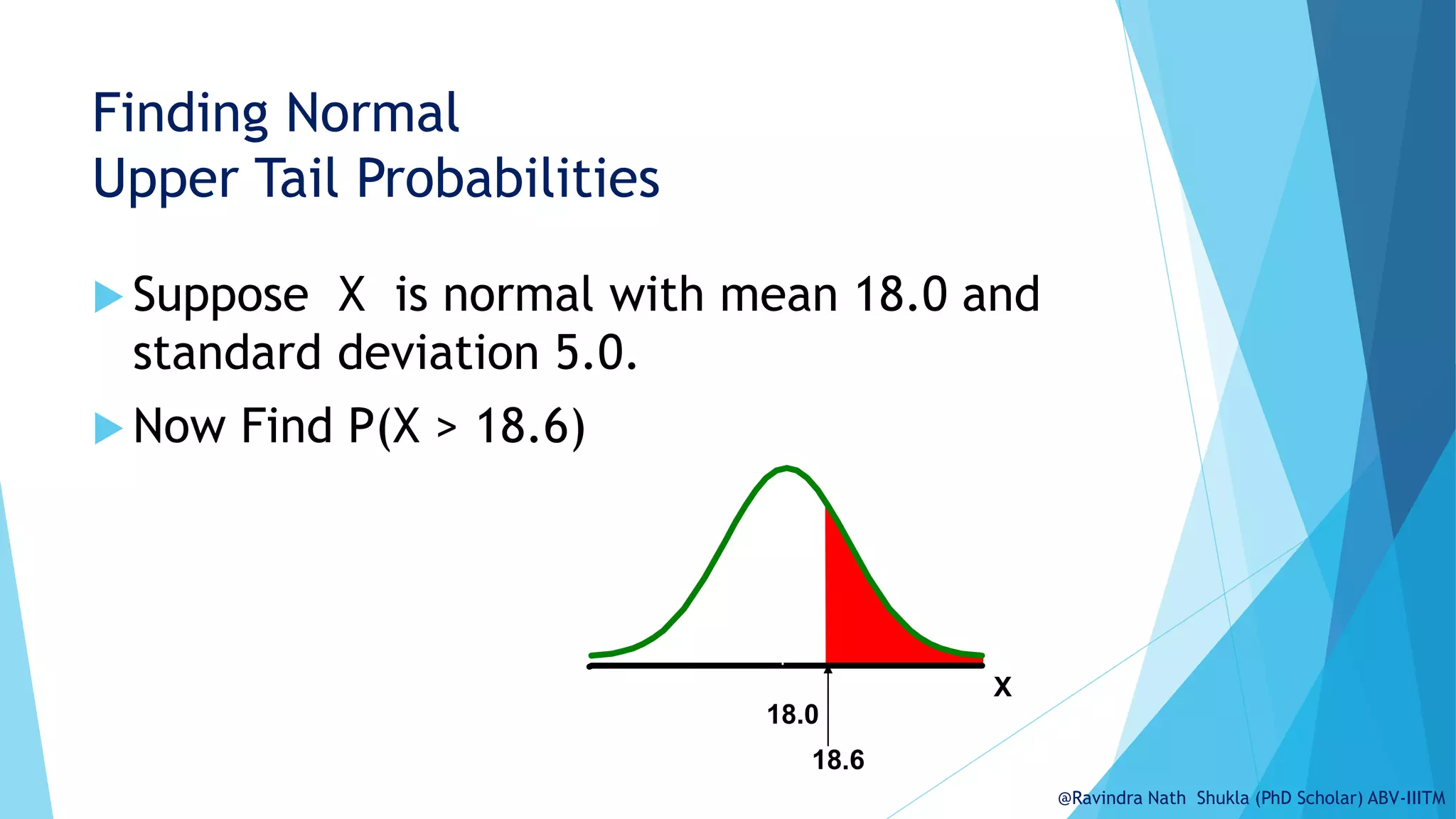
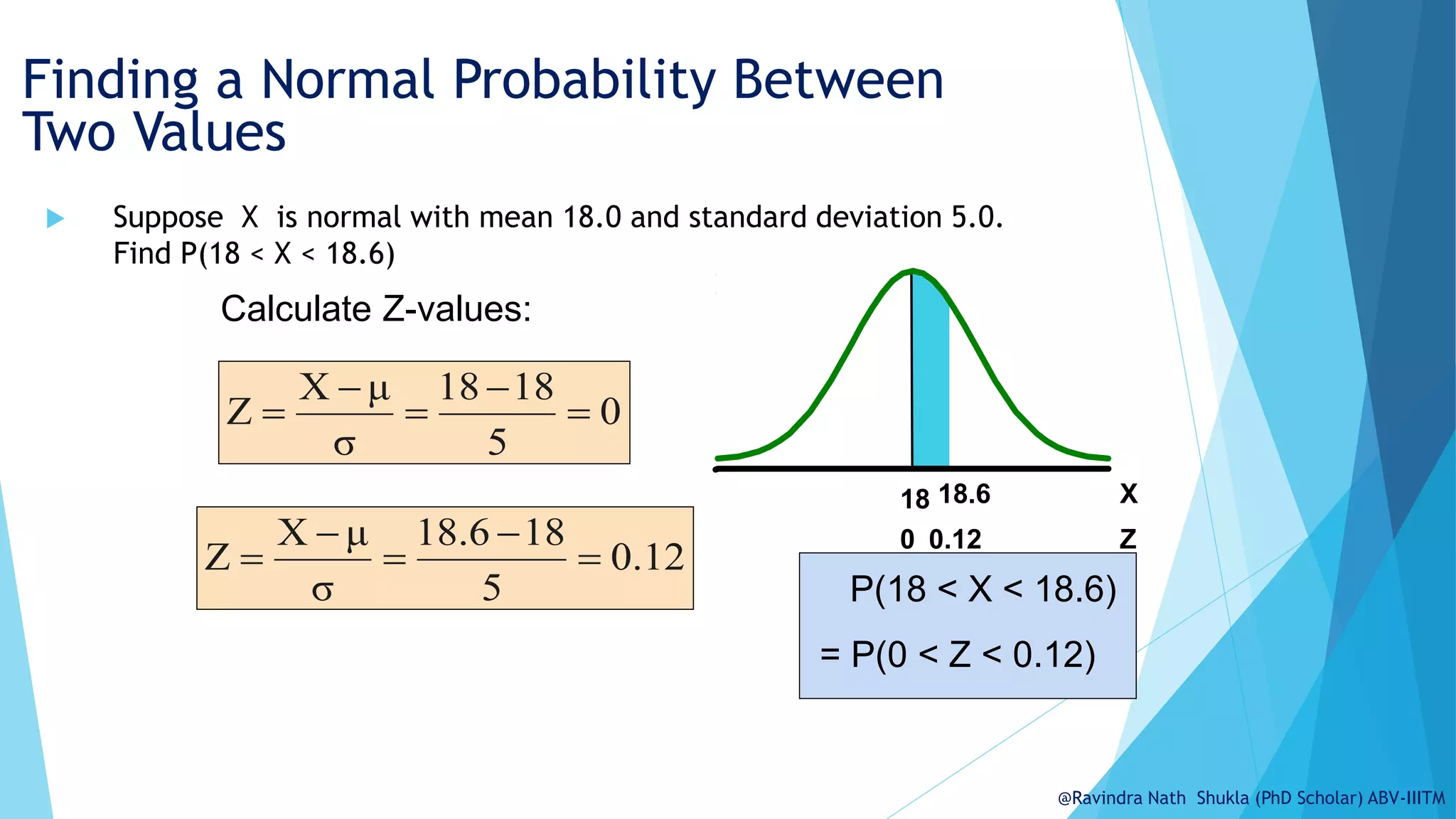
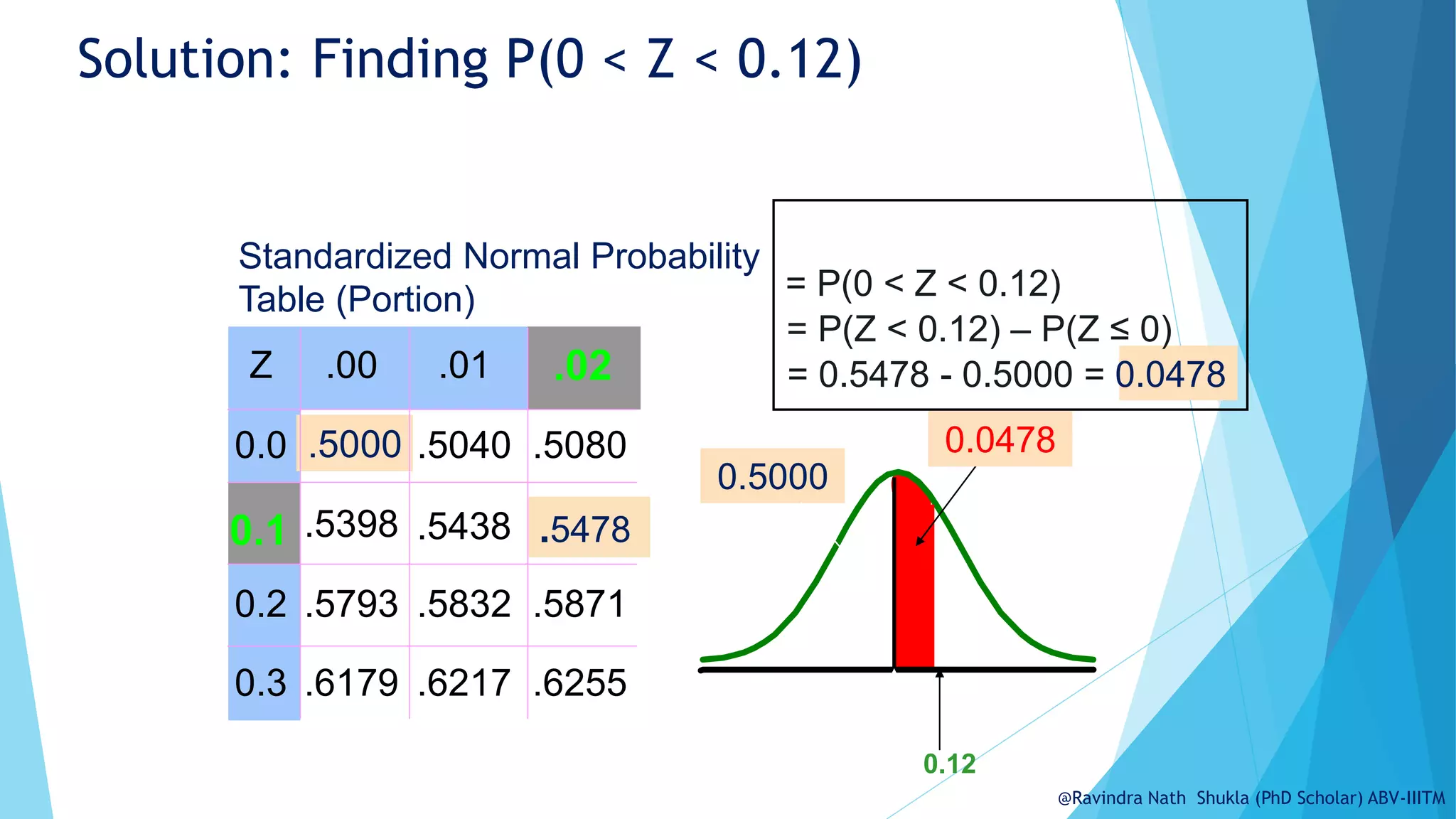
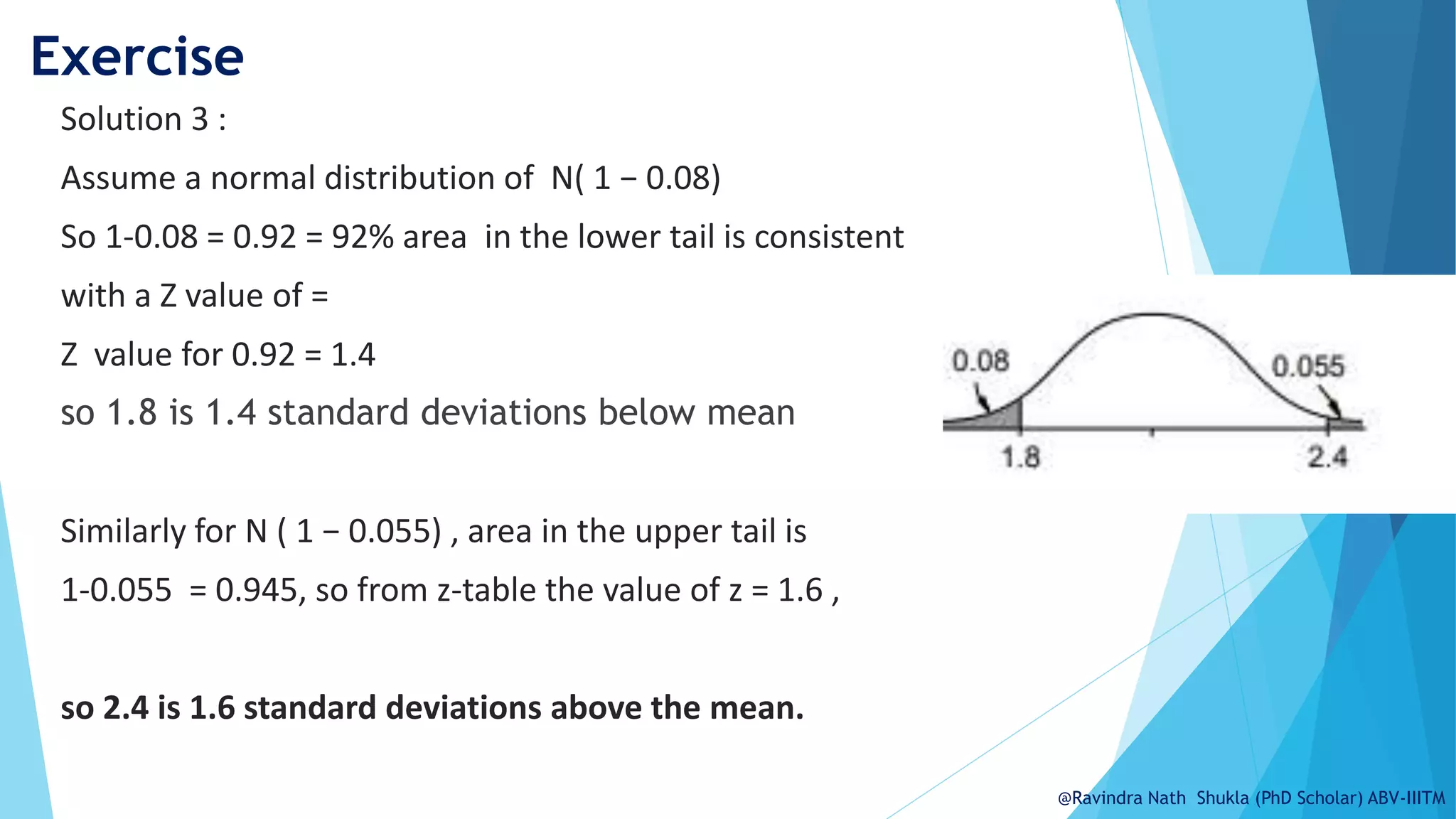
The document explains the normal distribution, emphasizing its significance as a continuous probability distribution described by a symmetric, bell-shaped curve. It covers key concepts such as mean, standard deviation, and the probability density function, along with methods for calculating probabilities and transforming values using standardized normal distribution (z-scores). Additionally, it discusses the empirical rule which outlines the proportion of data falling within one, two, and three standard deviations from the mean.