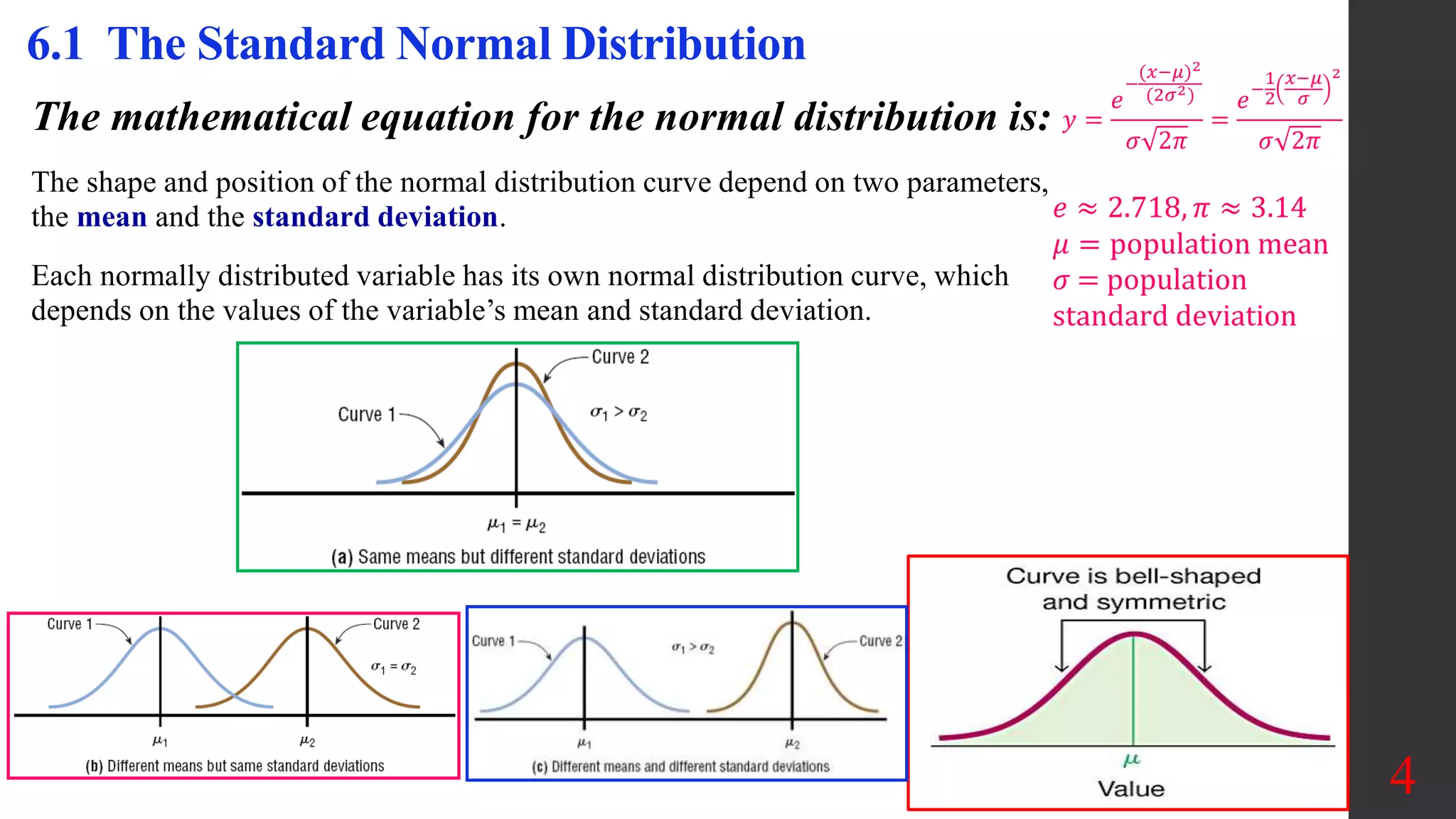
Chapter 6 covers the normal probability distribution, focusing on the standard normal distribution, its properties, and practical applications. It discusses identifying normal distributions, calculating areas under the curve, using the central limit theorem, and applying normal approximation to binomial variables. The chapter emphasizes the relationship between z-scores and areas, and provides tools for finding probabilities related to normally distributed data.

1. Elementary Statistics
Chapter 6:
Normal Probability
Distribution
6.1 The Standard
Normal Distribution
1

2. Chapter 6: Normal Probability Distribution
6.1 The Standard Normal Distribution
6.2 Real Applications of Normal Distributions
6.3 Sampling Distributions and Estimators
6.4 The Central Limit Theorem
6.5 Assessing Normality
6.6 Normal as Approximation to Binomial
2
Objectives:
• Identify distributions as symmetric or skewed.
• Identify the properties of a normal distribution.
• Find the area under the standard normal distribution, given various z values.
• Find probabilities for a normally distributed variable by transforming it into a standard normal variable.
• Find specific data values for given percentages, using the standard normal distribution.
• Use the central limit theorem to solve problems involving sample means for large samples.
• Use the normal approximation to compute probabilities for a binomial variable.

3. 6.1 The Standard Normal Distribution
Normal Distribution
If a continuous random variable has a distribution with a graph that is
symmetric and bell-shaped, we say that it has a normal distribution.
3
Key Concept: the standard normal distribution is a specific normal distribution having
the following three properties:
1. Bell-shaped: The graph of the standard normal distribution is bell-shaped.
2. µ = 0: The standard normal distribution has a mean equal to 0.
3. σ = 1: The standard normal distribution has a standard deviation equal to 1.
In this section we develop the skill to find areas (or probabilities or relative frequencies)
corresponding to various regions under the graph of the standard normal distribution. In
addition, we find z scores that correspond to areas under the graph.
For a continuous random variable, the probability of a single value of x is always zero.

4. The mathematical equation for the normal distribution is:
The shape and position of the normal distribution curve depend on two parameters,
the mean and the standard deviation.
Each normally distributed variable has its own normal distribution curve, which
depends on the values of the variable’s mean and standard deviation.
4
6.1 The Standard Normal Distribution
𝑒 ≈ 2.718, 𝜋 ≈ 3.14
𝜇 = population mean
𝜎 = population
standard deviation
𝑦 =
𝑒
−
(𝑥−𝜇)2
(2𝜎2)
𝜎 2𝜋
=
𝑒
−
1
2
𝑥−𝜇
𝜎
2
𝜎 2𝜋

5. • The normal distribution curve is bell-shaped.
• The mean, median, and mode are equal and located at the center of the distribution.
• The normal distribution curve is Unimodal (i.e., it has only one mode).
• The curve is symmetrical about the mean, which is equivalent to saying that its shape
is the same on both sides of a vertical line passing through the center.
• The curve is continuous—i.e., there are no gaps or holes.
• The curve never touches the x-axis. Theoretically, no matter how far in either
direction the curve extends, it never meets the x-axis—but it gets increasingly
closer.
• The total area under the curve = 1.00 or 100%.
• The area under the normal curve that lies within
 one standard deviation of the mean is approximately 0.68 (68%).
 two standard deviations of the mean is approximately 0.95 (95%).
 three standard deviations of the mean is approximately 0.997 ( 99.7%).
5
6.1 The Standard Normal Distribution
𝑦 =
𝑒
−
(𝑥−𝜇)2
(2𝜎2)
𝜎 2𝜋

6. Uniform Distribution
A continuous random variable has a uniform distribution if its values are spread evenly
over the range of possibilities. The graph of a uniform distribution results in a rectangular
shape.
Properties of uniform distribution:
1. The area under the graph of a continuous probability distribution is equal to 1.
2. There is a correspondence between area and probability, so probabilities can be found by
identifying the corresponding areas in the graph using this formula for the area of a
rectangle:
Area = height × width
Density Curve:
 The graph of any continuous probability distribution is called a density curve, and any
density curve must satisfy the requirement that the total area under the curve is exactly 1.
Because the total area under any density curve is equal to 1, there is a correspondence
between area and probability.
6
Uniform Distribution
6.1 The Standard Normal Distribution

7. Example 1
At JFK airport in New York City, passengers arriving at the security checkpoint
have waiting times that are uniformly distributed between 0 minutes and 5
minutes. All of the different possible waiting times are equally likely. Waiting
times can be any value between 0 min and 5 min (it’s a continuous value), so it
is possible to have a waiting time of 1.234567 min. Find the probability that a
randomly selected passenger has a waiting time of at least 2 minutes.
7
Uniform Distribution
Given: The total area under the curve = 1.00, 𝑤𝑖𝑑𝑡ℎ = 5
Height (the probability) =
1
𝑤𝑖𝑑𝑡ℎ
→ ℎ =
1
5
= 0.2
Solution: P(wait time of at least 2 min) = P x ≥ 2 =
= height × width of shaded area in the figure = 0.2 × 3 = 0.6

8. Standard Normal Distribution: Parameters of µ = 0 and σ = 1
Since each normally distributed variable has its own mean and standard deviation, the
shape and location of these curves will vary. In practical applications, one would have
to have a table of areas under the curve for each variable. To simplify this, statisticians
use the standard normal distribution.
We can find areas (probabilities) for different regions under a normal model using
technology or a Z-Table. Calculators and software generally give more accurate results
than a Z-Table.
8
6.1 The Standard Normal Distribution
𝑧 =
value − mean
standard deviation
𝑧 =
𝑥 − 𝜇
𝜎

9. Formats Used for Finding Normal Distribution Areas
9
1. To the left of any z
value: Look up the z value in the
table and use the area given.
2. To the right of any
z value: Look up the z value
and subtract the area from 1.
3. Between two
z values: Look up
both z values and
subtract the
corresponding areas.

10. A bone mineral density test can help identify the presence or likelihood of osteoporosis
which is measured as a z score: ND (µ = 0 & σ = 1).
Q: A randomly selected adult undergoes a bone density test. Find the probability that
this person has a bone density test score less than 1.27.
10
Example 2 Normal Distribution
Locate 1.2 in the left column and 0.07 in the top row: Read the value
Interpretation: The probability that a randomly selected person
has a bone density test result below 1.27 is 0.8980 (Or: Conclude
that 89.80% of people have bone density levels below 1.27.
𝑃(𝑧 < 1.27) = 0.8980

11. P(a < z < b) denotes the probability that the z score is between a and b.
P(z > a) denotes the probability that the z score is greater than a.
P(z < a) denotes the probability that the z score is less than a.
11
SND: Standard Normal Distribution
Finding Areas from the z Scores
a. Find the area to the left of z = 2.06.
b. Find the area to the right of z = –1.19.
Example 3
𝑃(𝑧 < 2.06) = 0.9803
𝑃(𝑧 > −1.19) = 0.8830
TI Calculator:
Normal Distribution Area
1. 2nd + VARS
2. normalcdf(
3. 4 entries required
4. Left bound, Right
bound, value of the
Mean, Standard
deviation
5. Enter
6. For −∞, 𝒖𝒔𝒆 − 𝟏𝟎𝟎𝟎
7. For ∞, 𝒖𝒔𝒆 𝟏𝟎𝟎𝟎

12. 12
a. Find the area between z = +1.68 and z = –1.37.
b. Find the probability: P(0 < z < 2.32)
Example 4 SND: Standard Normal Distribution
𝑃(0 < 𝑧 < 2.32) =
𝑃(−1.37 < 𝑧 < 1.68) =
0.9535 − 0.0853 = 0.8682
= 0.9898 − 0.5 = 0.4898

13. Using the same bone density test
ND (µ = 0 & σ = 1), find
a. the probability that a
randomly selected person has
a result above −1.00 (which
is considered to be in the
“normal” range of bone
density readings).
b. A bone density reading
between −1.00 and −2.50
indicates the subject has
osteopenia, which is some
bone loss. Find the
probability that a randomly
selected subject has a reading
between −1.00 and −2.50.
13
Example 5 Normal Distribution
1 − 0.1587
= 0.8413
𝑃(𝑧 > −1) =
Interpretation: The probability of randomly
selecting someone with a bone density reading
above −1 is 0.8413. We could also say that 84.13%
of people have bone density levels above −1.00.
𝑃(−2.5 < 𝑧 < −1) = 0.1525
Interpretation: There is a
probability of 0.1525 that a
randomly selected subject has a
bone density reading between −1.00
and −2.50. Or: 15.25% of people
have osteopenia (Weak Bones), with
bone density readings between
−1.00 and −2.50.

14. Notation & Finding z Scores from Known Areas
14
Draw a bell-shaped curve and identify the region under the curve that
corresponds to the given probability. If that region is not a cumulative region
from the left, work instead with a known region that is a cumulative region
from the left.
Use technology or the Z-Table find the z score. With Table A-2, use the
cumulative area from the left, locate the closest probability in the body of the
table, and identify the corresponding z score.
Critical Value: For the standard normal distribution, a critical value is a z
score on the borderline separating those z scores that are significantly low or
significantly high.
Notation: The expression zα denotes the z score with an area of α to its right.

15. Find the value of z0.025. (Let α = 0.025 in the expression zα.)
15
Example 6 Normal Distribution
Solution
The notation of z0.025 is used to represent the z score with an area of 0.025 to its right.
Note: that the value of z = 1.96 has an area of 0.025 to its right, so z0.025 = 1.96.
Note that z0.025 corresponds to a cumulative left area of 0.975.
CAUTION:
When finding a value of zα for a particular value of α, note that α is the area to the right of zα,
but the Table and some technologies give cumulative areas to the left of a given z score. To
find the value of zα, resolve that conflict by using the value of 1 − α. For example, to find z0.1,
refer to the z score with an area of 0.9 to its left.
TI Calculator:
Normal Distribution: find
the Z-score
1. 2nd + VARS
2. invNorm(
3. 3 entries required
4. Left Area, value of the
Mean, Standard
deviation
5. Enter

16. 16
Find the z value such that
a. the area under the standard normal distribution
curve between 0 and the z value is 0.2123.
b. Find 𝑃10, the 10th percentile.
Example 7 SND: Standard Normal Distribution
𝑃(0 < 𝑧 < 𝑧 − 𝑣𝑎𝑙𝑢𝑒) = 0.2123
Add 0.5000 to 0.2123 to get the
cumulative area = 0.7123, why?
The z value is 0.56.
𝑃10 = −1.28, why?
Area = 𝟏𝟎% = 𝟎. 𝟏