This document summarizes Newton's method, an iterative process for finding approximations of the zeroes of a function. It works by using tangent lines to get better approximations with each iteration. The method starts with an initial guess x1 and calculates successive approximations x2, x3, etc. by finding the x-intercept of the tangent line at the previous point. If the approximations converge to a limit, Newton's method has found a zero of the function. The document provides examples of functions where Newton's method does and does not converge.

1. Approximate a zero of a function using Newton’s Method

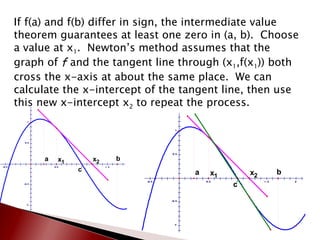
2. This method, named Newton’s Method, uses tangent lines to approximate the value of the x-intercepts of a function. Consider a function that is continuous on interval [a, b]. If the graph crosses the x-axis somewhere between a and b, or in other words, if f(a) and f(b) are different signs, then a tangent line crosses the x-axis at about the same location as the actual x-intercept of f .

3. If f(a) and f(b) differ in sign, the intermediate value theorem guarantees at least one zero in (a, b). Choose a value at x 1 . Newton’s method assumes that the graph of f and the tangent line through (x 1 ,f(x 1 )) both cross the x-axis at about the same place. We can calculate the x-intercept of the tangent line, then use this new x-intercept x 2 to repeat the process.

4. By the third x-intercept from a tangent, we are SOOOO close to the actual x-intercept for f. Here’s the math behind things. The tangent line through (x 1 , f(x 1 )) with a slope of f’(x 1 ) is Letting y = 0 and solving for x: This new x we’ll call x 2: Repeat again and we get: This repeated application is called Newton’s Method.

5. This process could be how the calculator is solving for zeros.

6. Isaac Newton wrote about his method in 1671 in a text called Method of Fluxions . It wasn’t published until 1736, and another man, Joseph Raphson published a paper in 1690 describing a method very similar to Newton’s. So this method is often called the Newton-Raphson method. Luckily for us there is a calculator program that will apply Newton’s Method for us and count how many repeated times it is applied, the iterations. It is on the list of programs that you already have been given.

7. I also found a calc program for the TI-83/84 that shows all the table values and works well. I entitled it NEWTON2, so come and get that one if you would like. This would be especially helpful if you are planning on taking the AP Calculus exam, where they expect you to show each iteration and the values you get that way. I didn’t find one like this for TI-86, but if you find one, let me know. If each subsequent approximations approach some limit, the sequence x 1 , x 2 , x 3 , . . . X n ,. . . is said to converge . Newton’s method doesn’t give you answers if the process doesn’t result in a convergent sequence. One way it fails is if f’(x n ) is zero. Usually you can overcome that by choosing a different initial guess.

8. Another way it fails is by having an x-intercept where the function’s derivative is not defined. Ex 3 p.231 The function: The derivative: The method: In this case, x n continues to increase in absolute value, switching between negative and positive, so the limit of the sequence doesn’t exist.

9. Condition for convergence: for interval. For f(x) = x 2 -2, f’(x) = 2x, f”(x) = 2, So you can find zero. So you can’t find zero with Newton’s method for any interval.

10. 3.8 p. 233/ 5-18, 21-24 (find approximations)