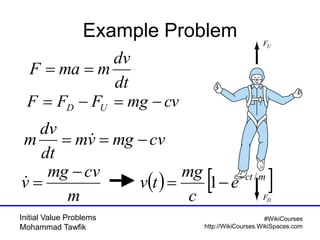
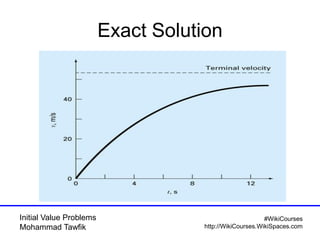
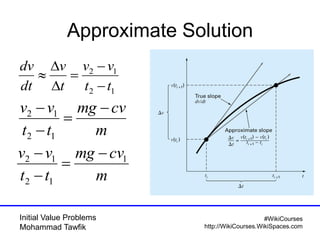
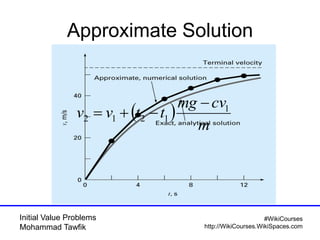
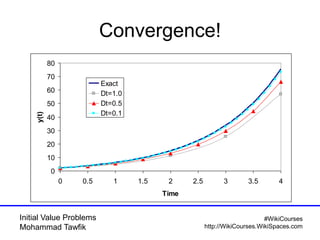
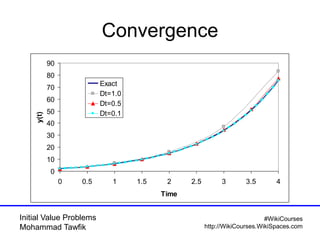
The document covers initial value problems and methods for solving them, particularly focusing on the Euler method and the Runge-Kutta methods. It provides examples and mathematical formulations for applying these methods to specific differential equations, along with convergence analysis. Additionally, it includes assignments for further practice on the discussed methods.

1. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Initial Value Problems
Mohammad Tawfik

2. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Objectives
• Understand the applications of initial-value
problems
• Be able to apply the Euler method for
solving initial value problems
• Be able to apply the Runge-Kutta method
for solving initial value problem

3. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Example Problem
dt
dv
mmaF 
cvmgFFF UD 
cvmgvm
dt
dv
m  
m
cvmg
v

    mct
e
c
mg
tv /
1 


4. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Exact Solution

5. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Approximate Solution
12
12
tt
vv
t
v
dt
dv






m
cvmg
tt
vv 



12
12
m
cvmg
tt
vv 1
12
12 




6. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Approximate Solution
 
m
cvmg
ttvv 1
1212



7. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Euler Method
• Given the differential
equation:
• We may write:
• Giving:
 tyf
dt
dy
,
 tyf
t
yy
t
y
dt
dy ttt
,





 
 tytfyy ttt ,

8. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Example
• Given the differential
equation:
• The exact solution is:
• At t=0, y=2
• Find y(4) using Euler
method with step
t=1
ye
dt
dy t
5.04 8.0

  tt
eety 5.08.0
08.108.3 


9. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Solution
ye
dt
dy t
5.04 8.0
  yetyy t
tttt 5.04 8.0
 
 
  5142
5.04 0
0
01

 yeyy  
  4.115.245
5.04
8.0
1
8.0
12


e
yeyy
 
  5.254.11*5.044.11
5.04
6.1
2
2*8.0
23


e
yeyy
 
  8.565.25*5.045.25
5.04
4.2
3
3*8.0
34


e
yeyy

10. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Convergence!
0
10
20
30
40
50
60
70
80
0 0.5 1 1.5 2 2.5 3 3.5 4
Time
y(t)
Exact
Dt=1.0
Dt=0.5
Dt=0.1

11. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Runge-Kutta Methods
• The Runge-Kutta methods achieves the
Taylor series accuracy
• Many forms of the method are available;
we will use 2nd order and 3rd order
methods only

12. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
2nd Order Runge-Kutta method
• For the DE:
• The 2nd order R.K. solution
is:
• Where:
 tyf
dt
dy
,
 21
2
kk
t
yy ttt 


 tyfk t ,1 
 tttkyfk t  ,12

13. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Example
• Given the differential
equation:
• The exact solution is:
• At t=0, y=2
• Find y(4) using 2nd
order R.K. method
with step t=1
ye
dt
dy t
5.04 8.0

  tt
eety 5.08.0
08.108.3 


14. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Solution
• At t=0
32*5.04 0
1  ek
 
  4.61*325.04 108.0
2  
ek
  7.6
2
2101 

 kk
t
yy
• Repeat for all t

15. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Solution
yk2k1t
20
6.7010826.40216431
16.3197813.685785.5516232
37.1992530.106711.652243
83.3377766.7839625.493084
yk2k1t
20
3.8043254.21729930.5
6.3165385.9837174.0651361
9.9240688.6862255.7438951.5
15.196312.770498.3184342
22.9759418.9045812.213982.5
34.5149228.0876718.068263
51.6768141.8123226.835253.5
77.2385262.3066739.940184

16. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Convergence
0
10
20
30
40
50
60
70
80
90
0 0.5 1 1.5 2 2.5 3 3.5 4
Time
y(t)
Exact
Dt=1.0
Dt=0.5
Dt=0.1

17. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
3rd Order Runge-Kutta method
• For the DE:
• The 3rd order R.K.
solution is:
• Where:
 tyf
dt
dy
,
 321 4
6
kkk
t
yy ttt 


 tyfk t ,1 





 



2
,
2
1
2
t
t
tk
yfk t
 tttktkyfk t  ,2 213

18. Initial Value Problems
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Assignment
• Solve:
• Given y(0)=1
1. Analytically
2. Using Euler method until t=2, with t=0.5
3. Repeat part 2 using 2nd order RK method
4. Repeat part 2 using 3rd order RK method
5. Repeat parts 2 through 4 using t=0.25
6. Compare results of all parts above
yyt
dt
dy
2.12
