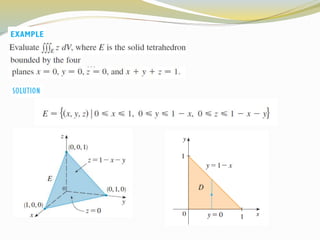
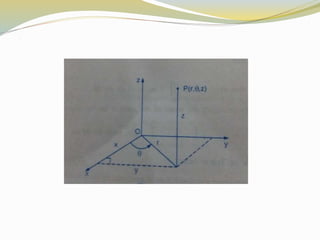
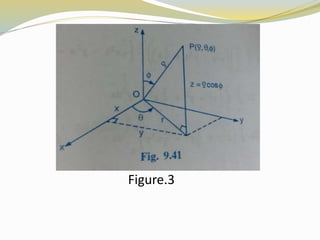
This document discusses triple integrals and their evaluation in different coordinate systems. It begins by defining a triple integral as the generalization of a double integral to three dimensions. It then discusses evaluating triple integrals in rectangular, cylindrical, and spherical coordinate systems. For each system it provides the coordinate transformations between rectangular and the other system and the formula for the volume element used in the triple integral.

1. L. D. College Of Engineering,
Ahmedabad

2. Calculus
Multiple Integrals
- Triple Integrals

3. Index:-
Triple Integrals
Triple Integrals in Cylindrical Co-
ordinates
Triple Integrals in Spherical Co-
ordinates
Change of order of Integration
Jacobian of several variables

4. Triple Integrals:
The triple integral is defined in a similar manner to that
of the double integral if f(x,y,z) is continuous and
single-valued function of x, y, z over the region R of
space enclosed by the surface S. We sub divide the
region R into rectangular cells by planes parallel to the
three co-ordinate planes(fig 1).The parallelopiped cells
may have the dimensions of δx, δy and δz.We number
the cells inside R as δV1, δV2,…..δVn.

5. .
In each such parallelopiped cell we choose an arbitrary
point in the k th pareallelopiped cell whose volume is
δVk and then we form the sum
=

6. .

7. .

8. .

9. .

10. Triple Integrals In Cylindrical
Coordinates:
 We obtain cylindrical coordinates for space by
combining polar coordinates (r, θ) in the xy-plane with
the usual z-axis.
 This assigns every point in space one or more
coordinates triples of the form (r, θ, z) as shown in
figure.2.

11. .

12. Definition : Cylindrical coordinate
Cylindrical coordinate represent a point P in space by orders triples (r, θ, z) in which
1. (r, θ) are polar coordinates for the vertical projection of P on xy-plane.
2. z is the rectangular vertical coordinates.
The rectangular (x , y , z) and cylindrical coordinates are related by the
usual equations as follow :
x = r cosθ, y = r sinθ , z = z
𝑟2
= 𝑥2
+ 𝑦2
, tanθ =
𝑦
𝑥
.

13. Formula for tripple integral in
cylindrical coordinates
where,volume element in cylindrical coordinates is given
by dV = rdzdrdθ

14. Triple Integrals in Spherical Co-
ordinates:
 Spherical coordinates locate points in space is with two
angles and one distance, as shown in figure.3.
 The first coordinate P = |OP|, is the point’s
distance from the origin.
The second coordinate ф, is the angle OP make with the
positive z-axis.
It is required to lie in the interval 0 ≤ ф ≤ π.
The third coordinate is the angle θ as measured in
cylindrical coordinates.

15. Figure.3

16. Definition : Spherical coordinates
Spherical coordinates represent a point P in ordered triples (ƍ , θ , ф) in
which
1. ƍ is the distance from P to the origin.
2. θ is the angle from cylindrical coordinates.
3. ф is the angle OP makes with the positive z-axis (0 ≤ ф ≤ π).
The rectangular coordinates (x , y, z) and spherical coordinates are related
by the
following equations :
x = ƍ sinф cosθ , y = ƍ sinф sinθ, z = P cosф.

17. Formula for Triple integral in
spherical coordinates:-
where, D = {(ƍ , θ , ф) | a ≤ ƍ ≤ b, α ≤ θ ≤ β,
c ≤ ф ≤ d}
and dV = ƍ2 sin фdƍdф.