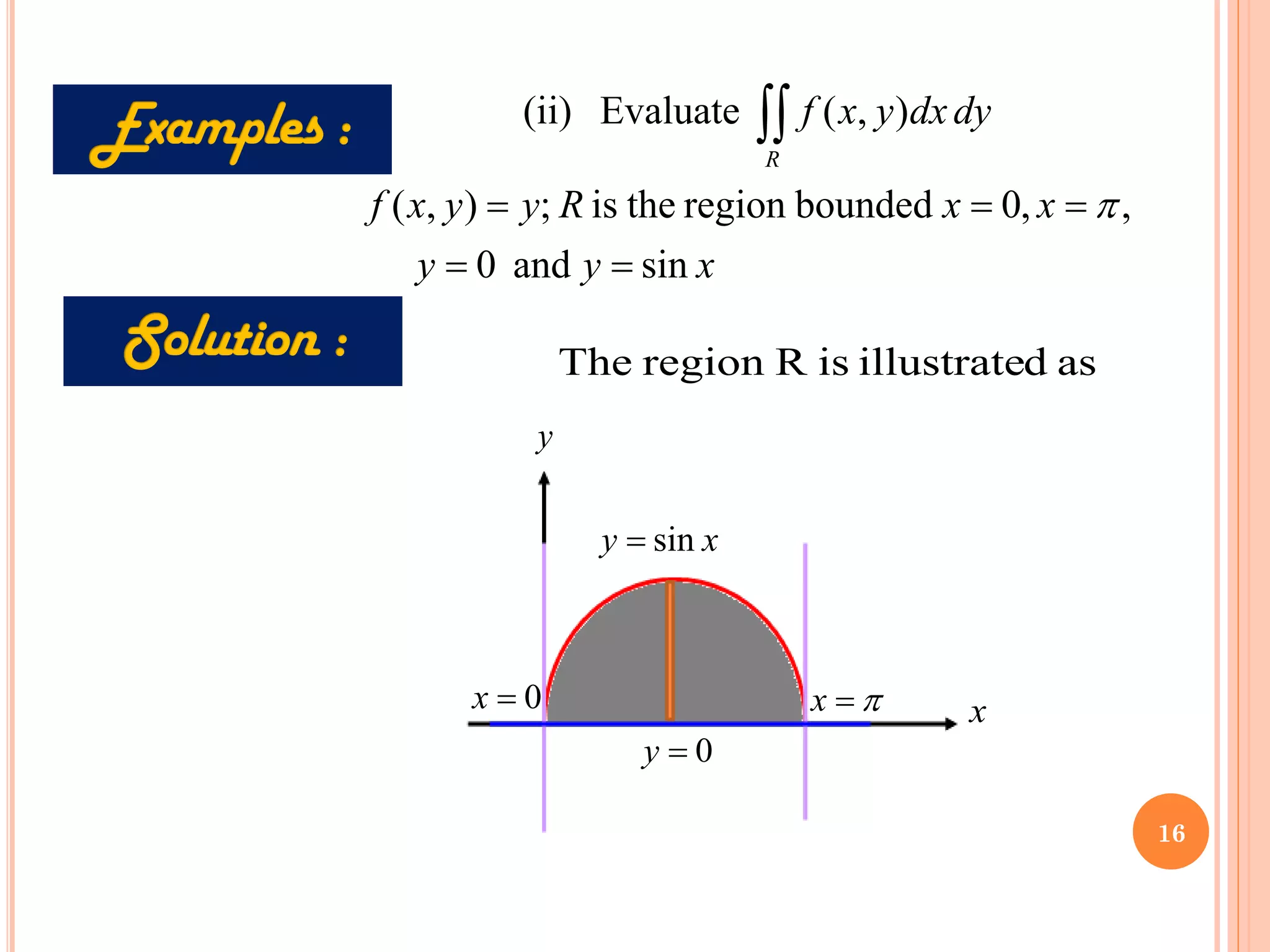
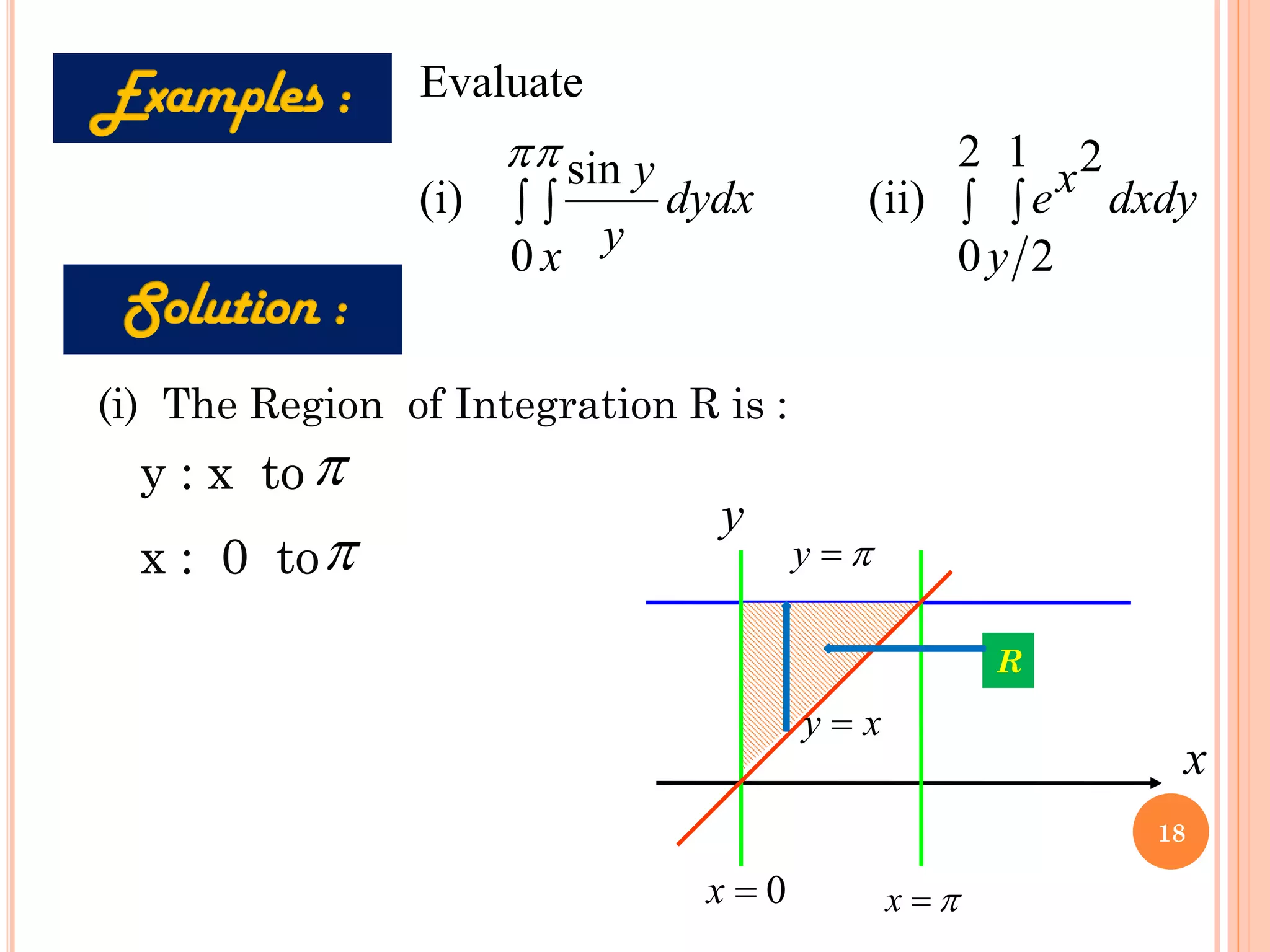
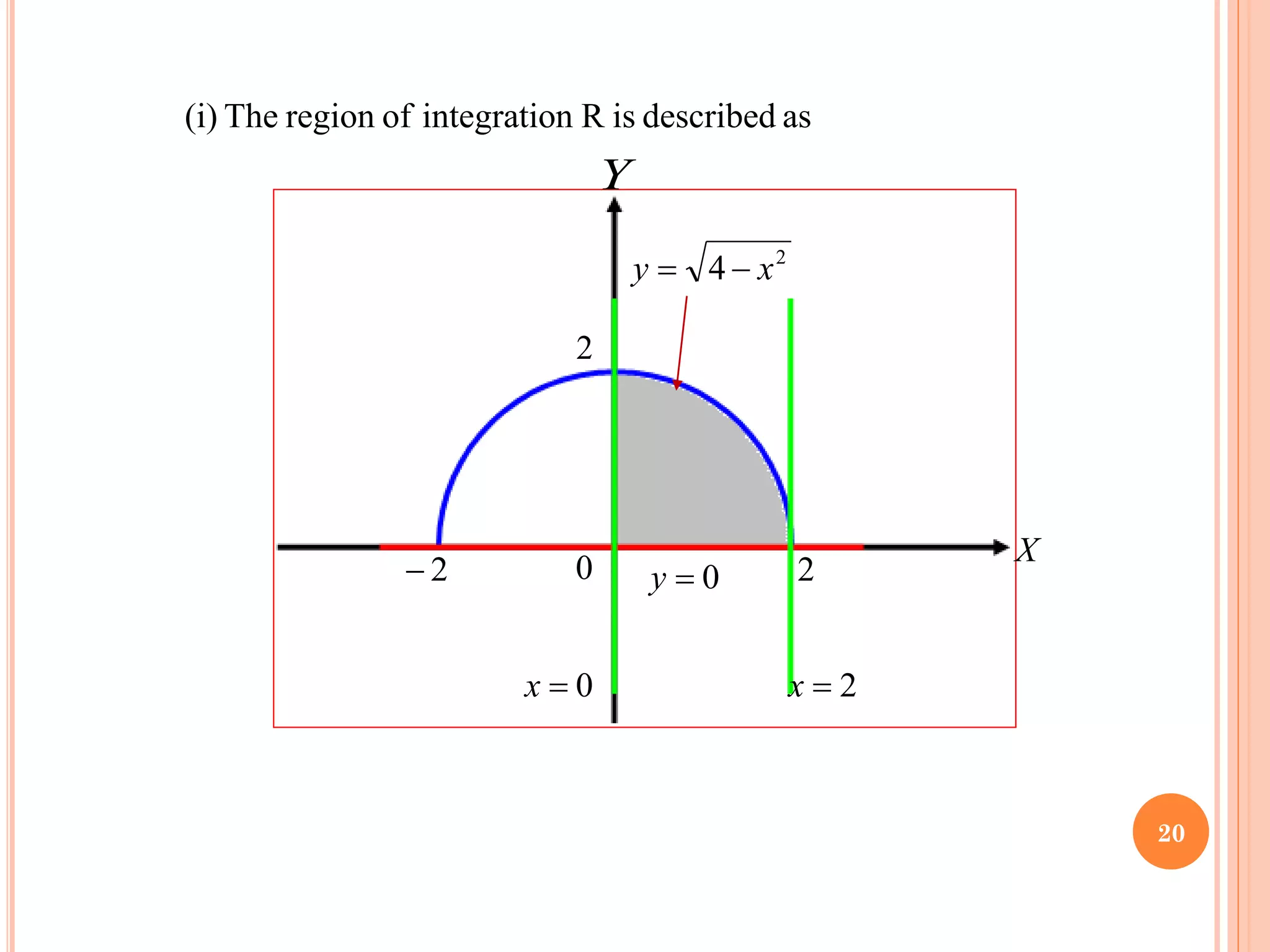
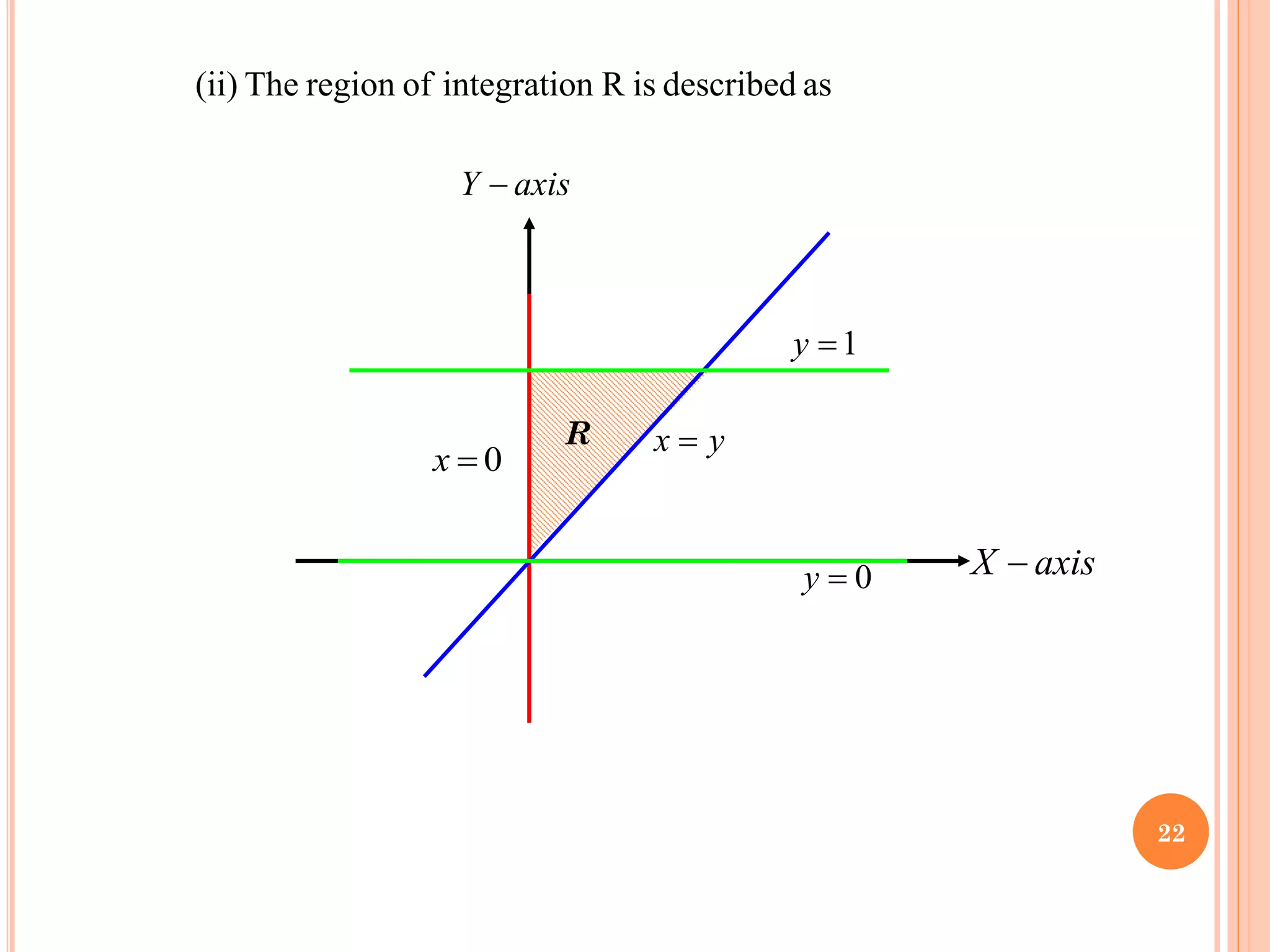
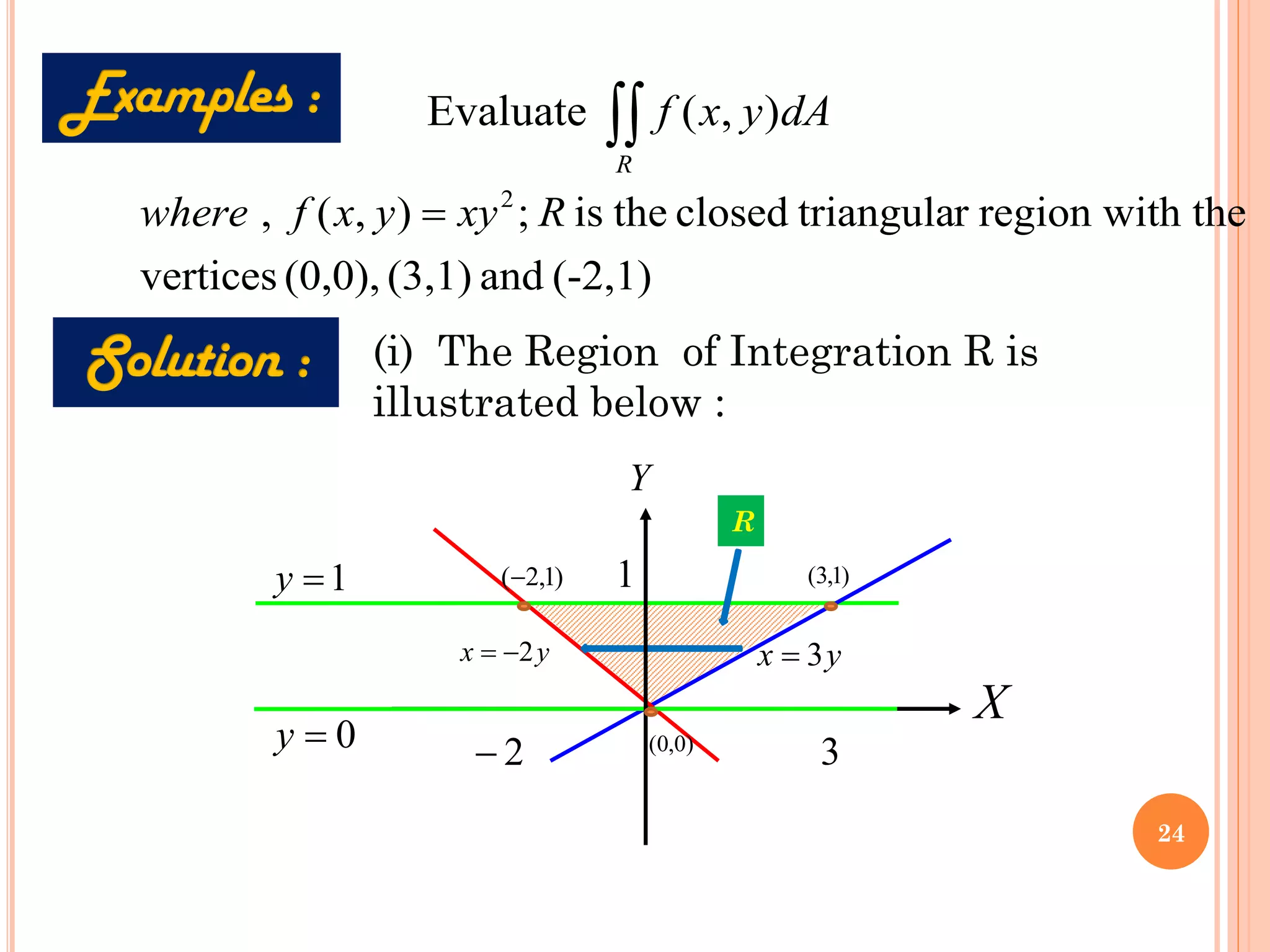
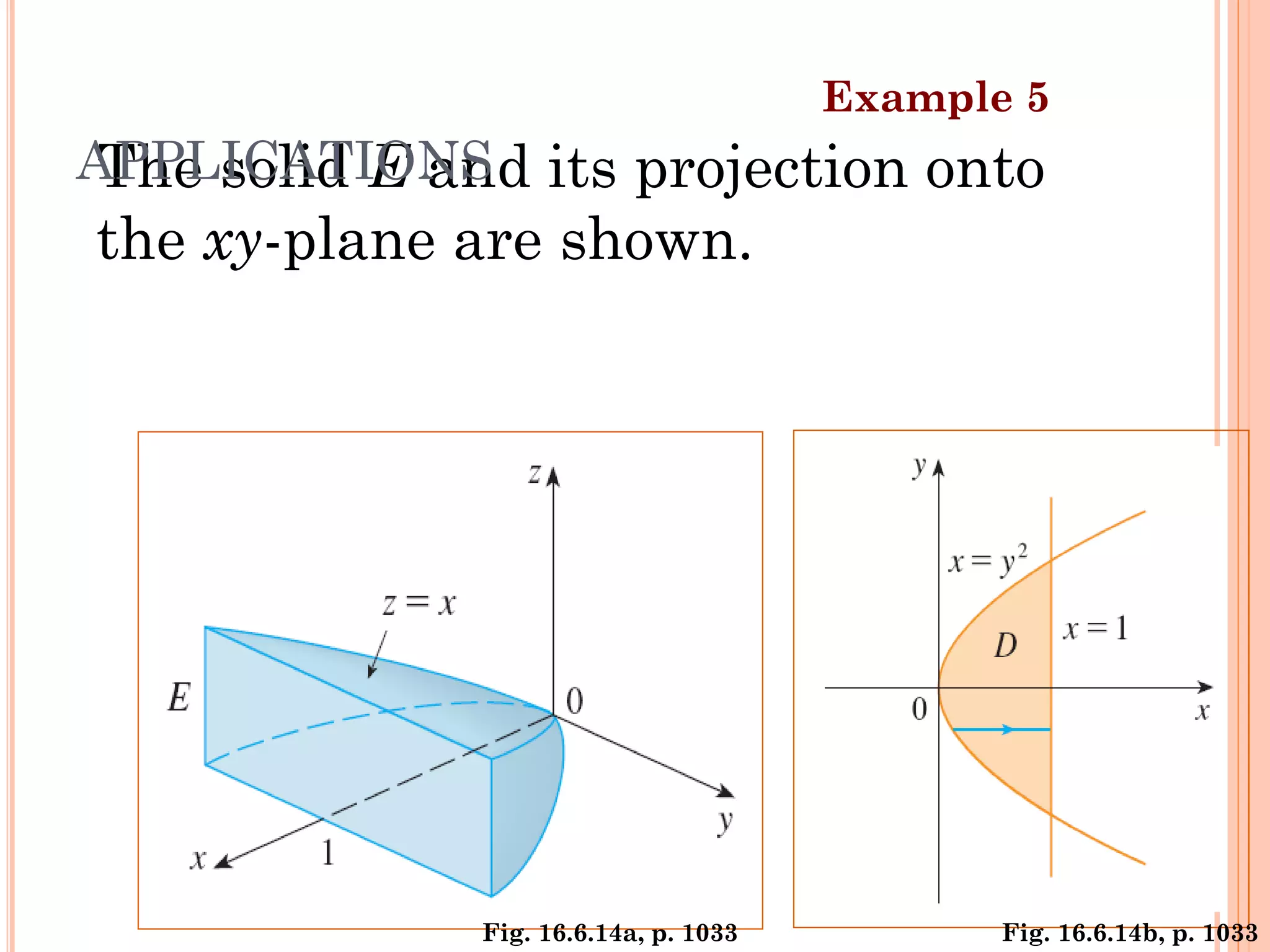
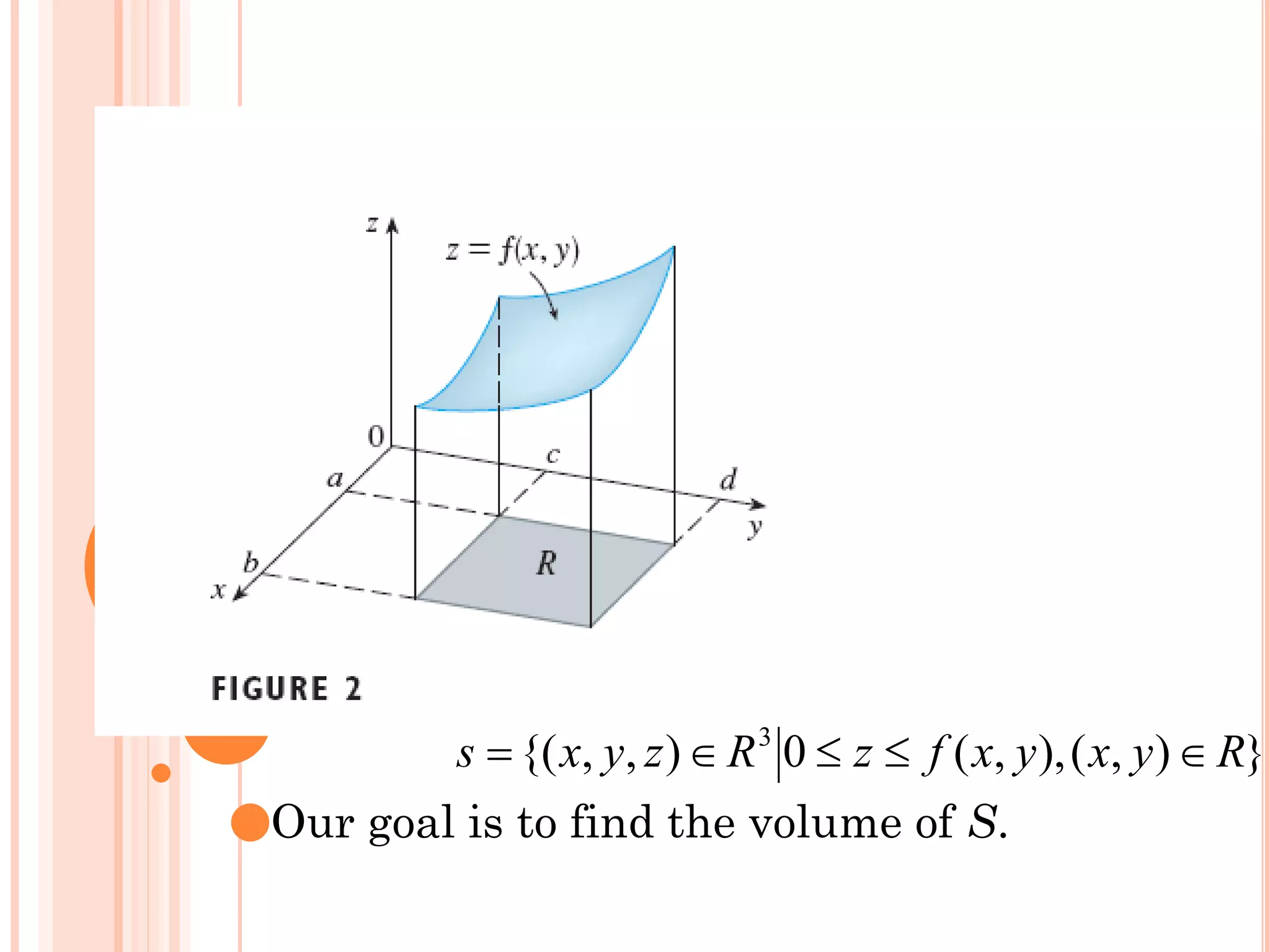
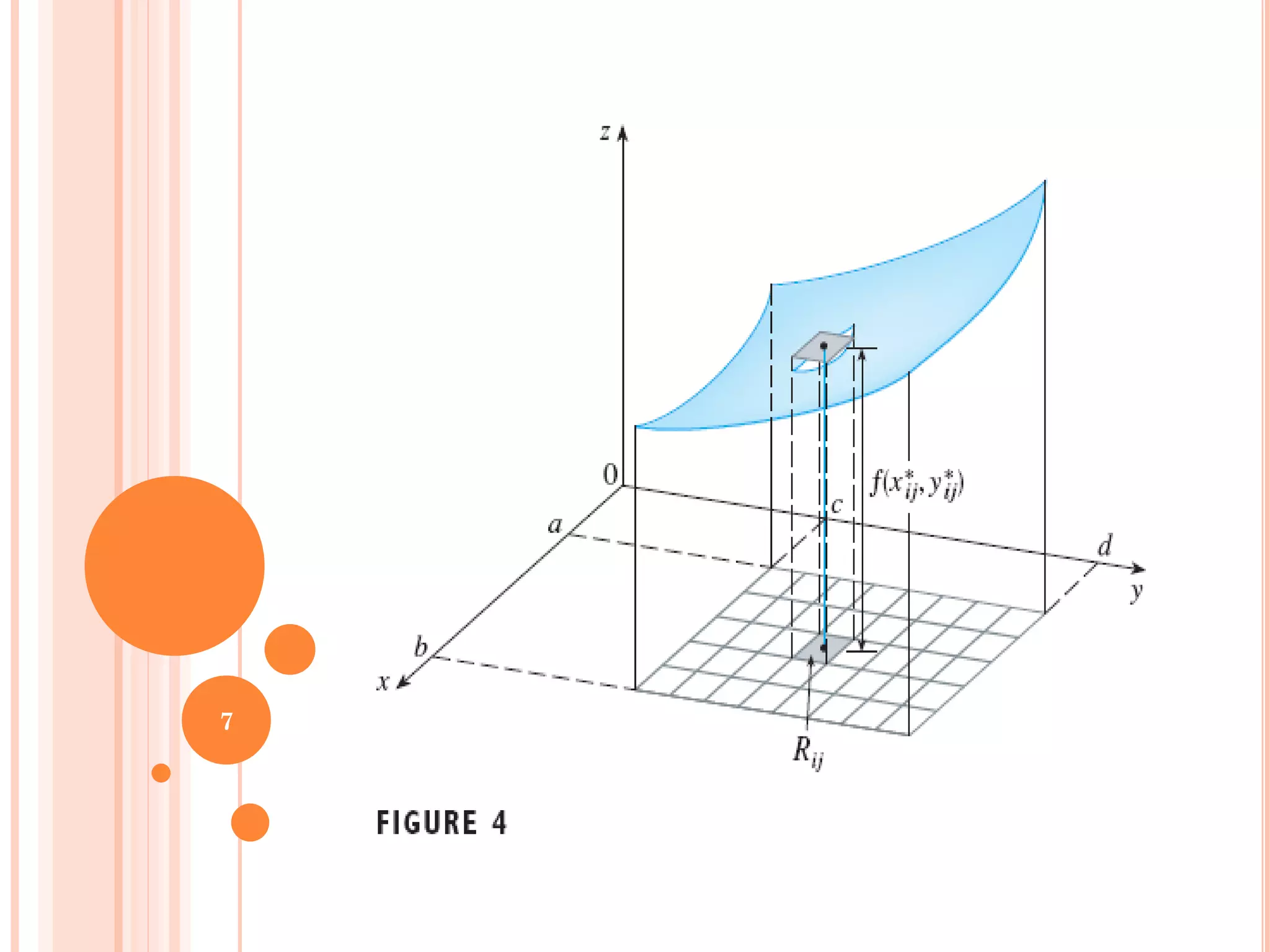
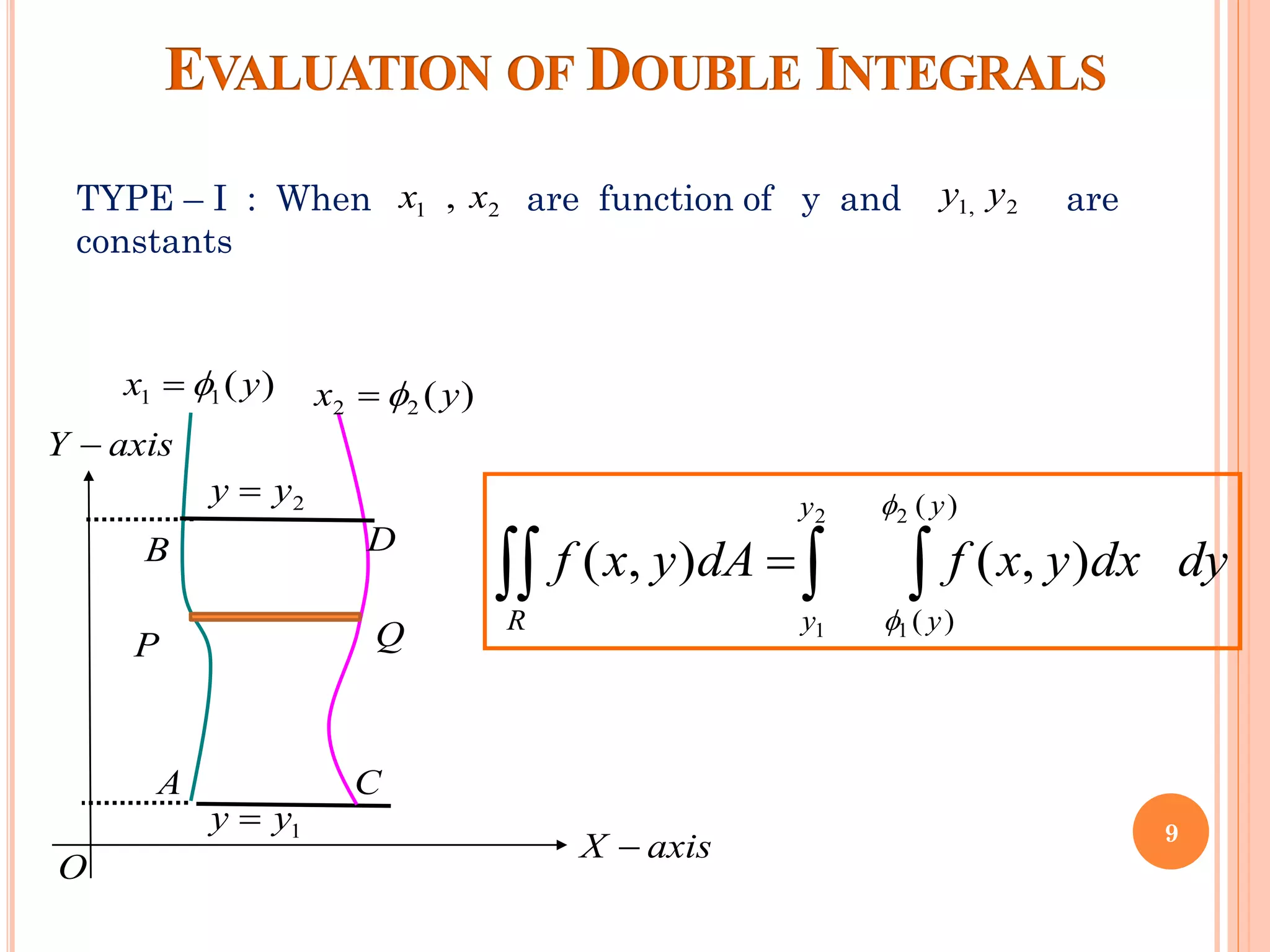
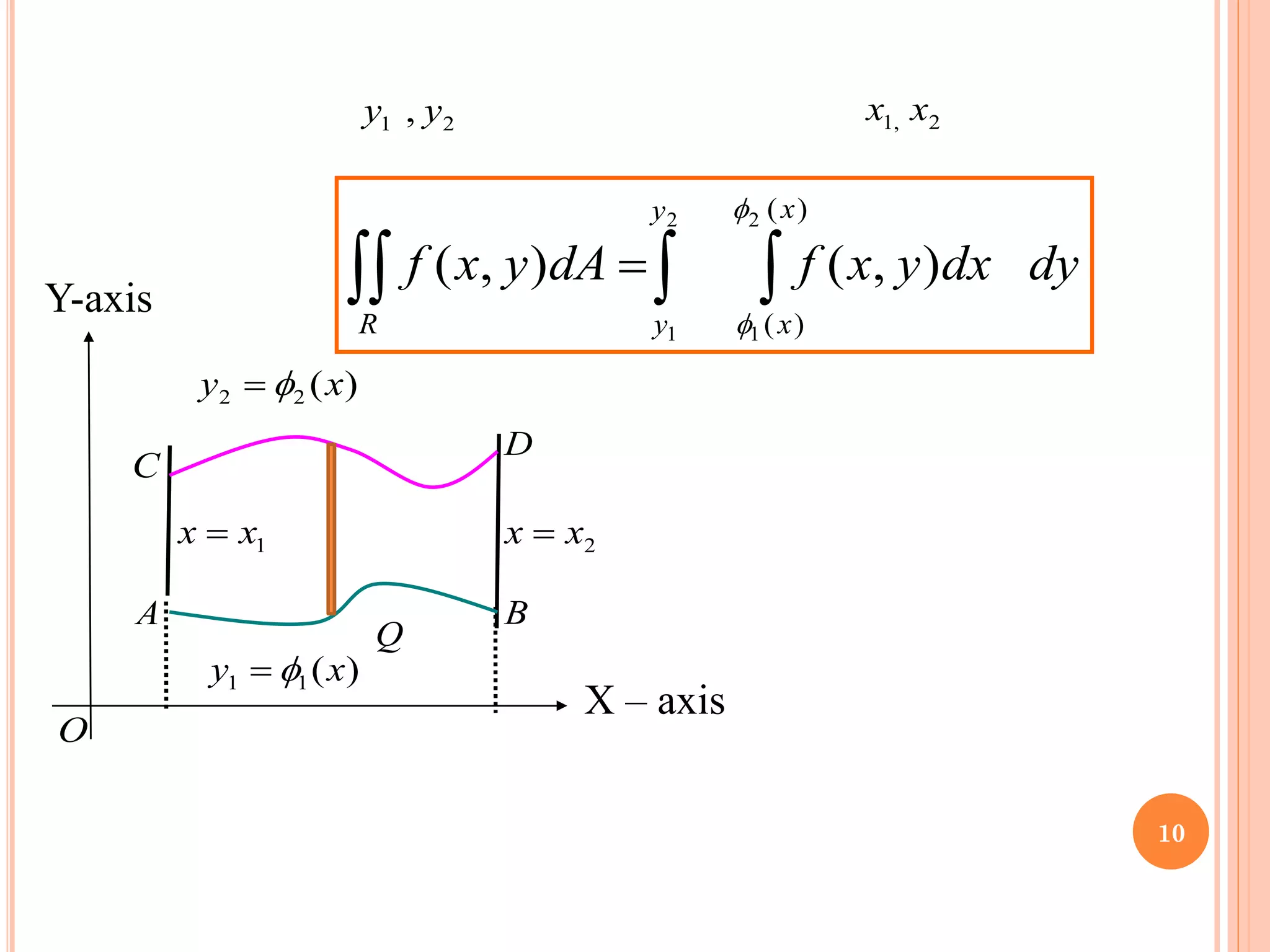
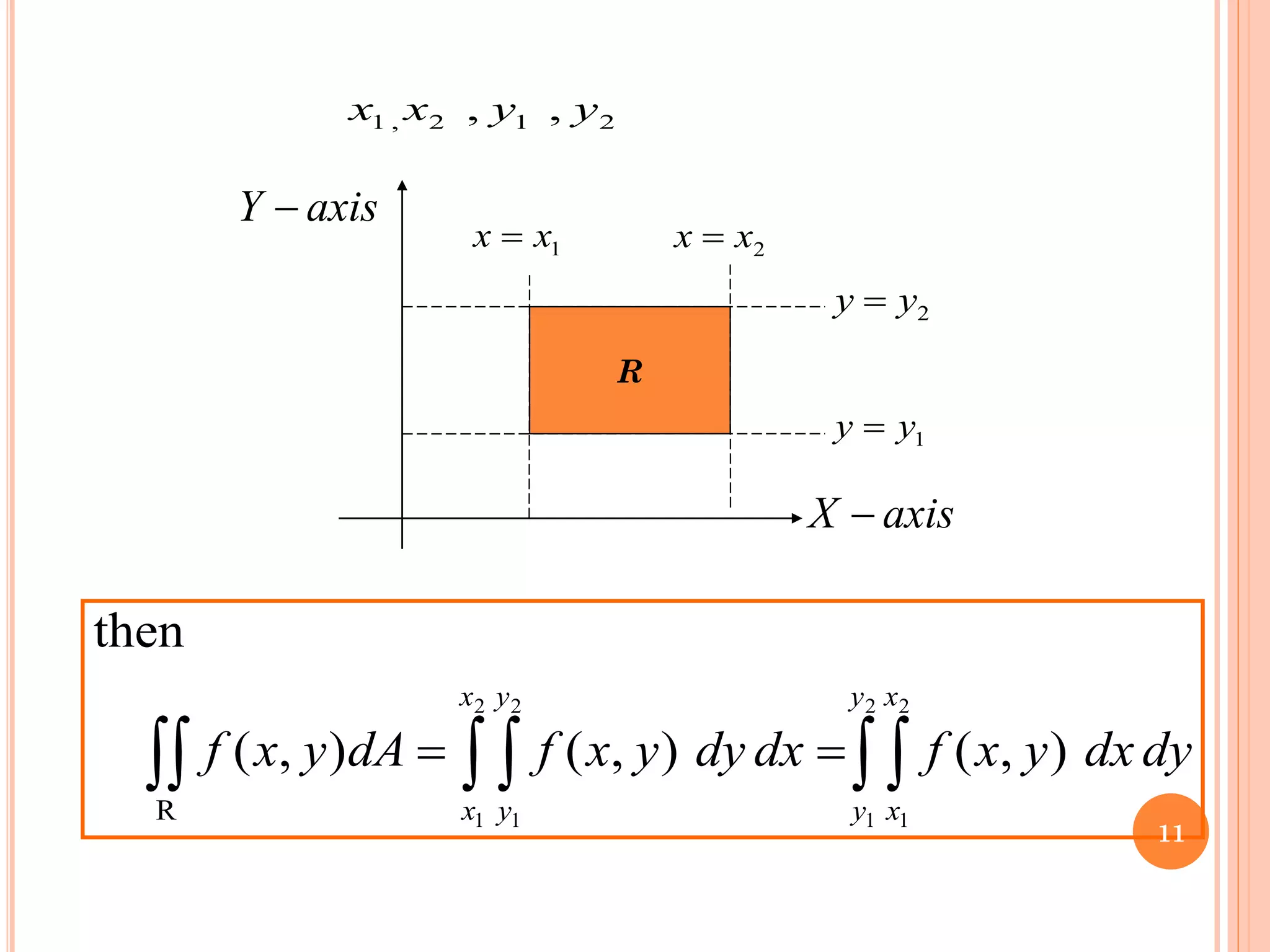
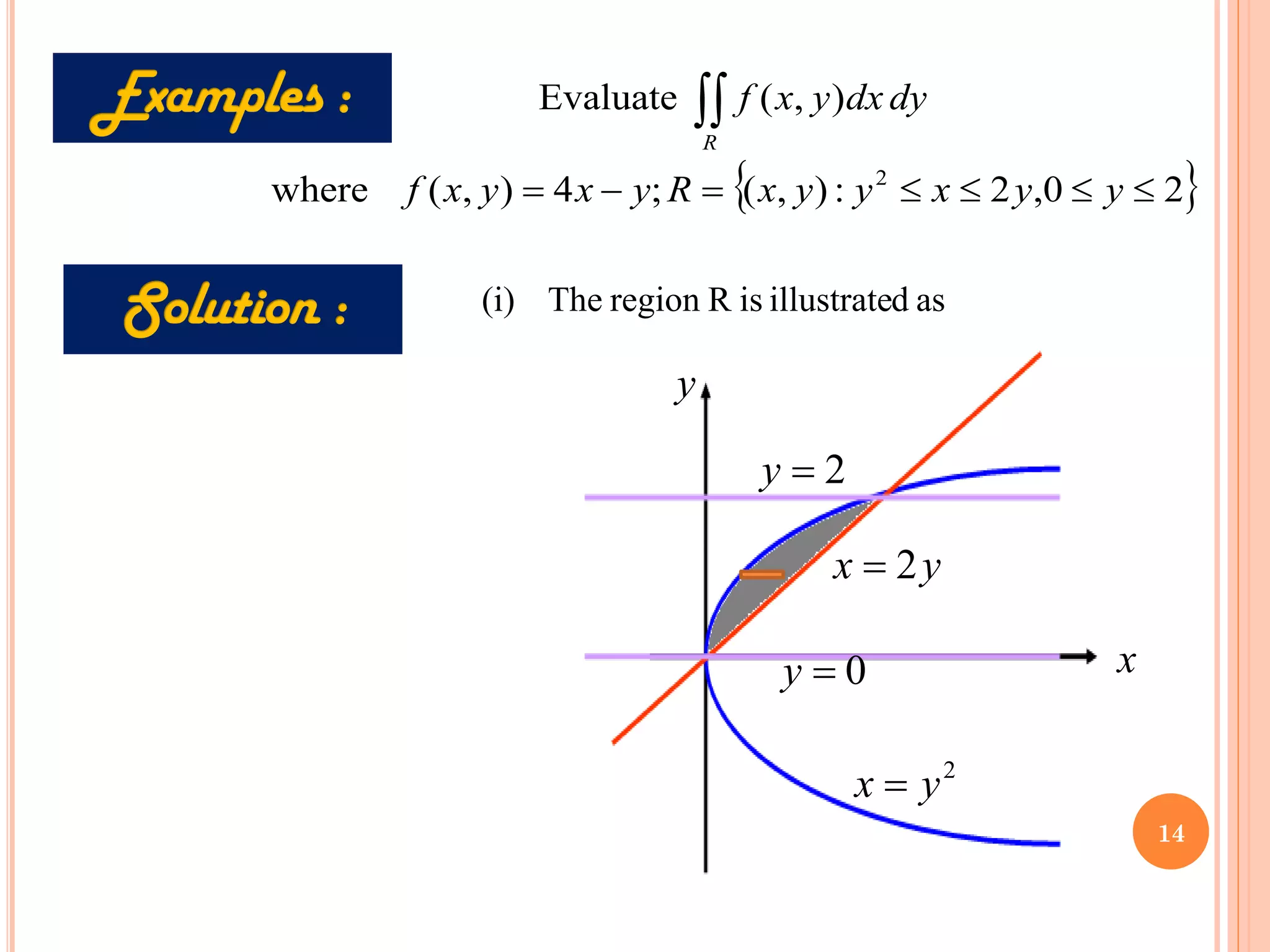
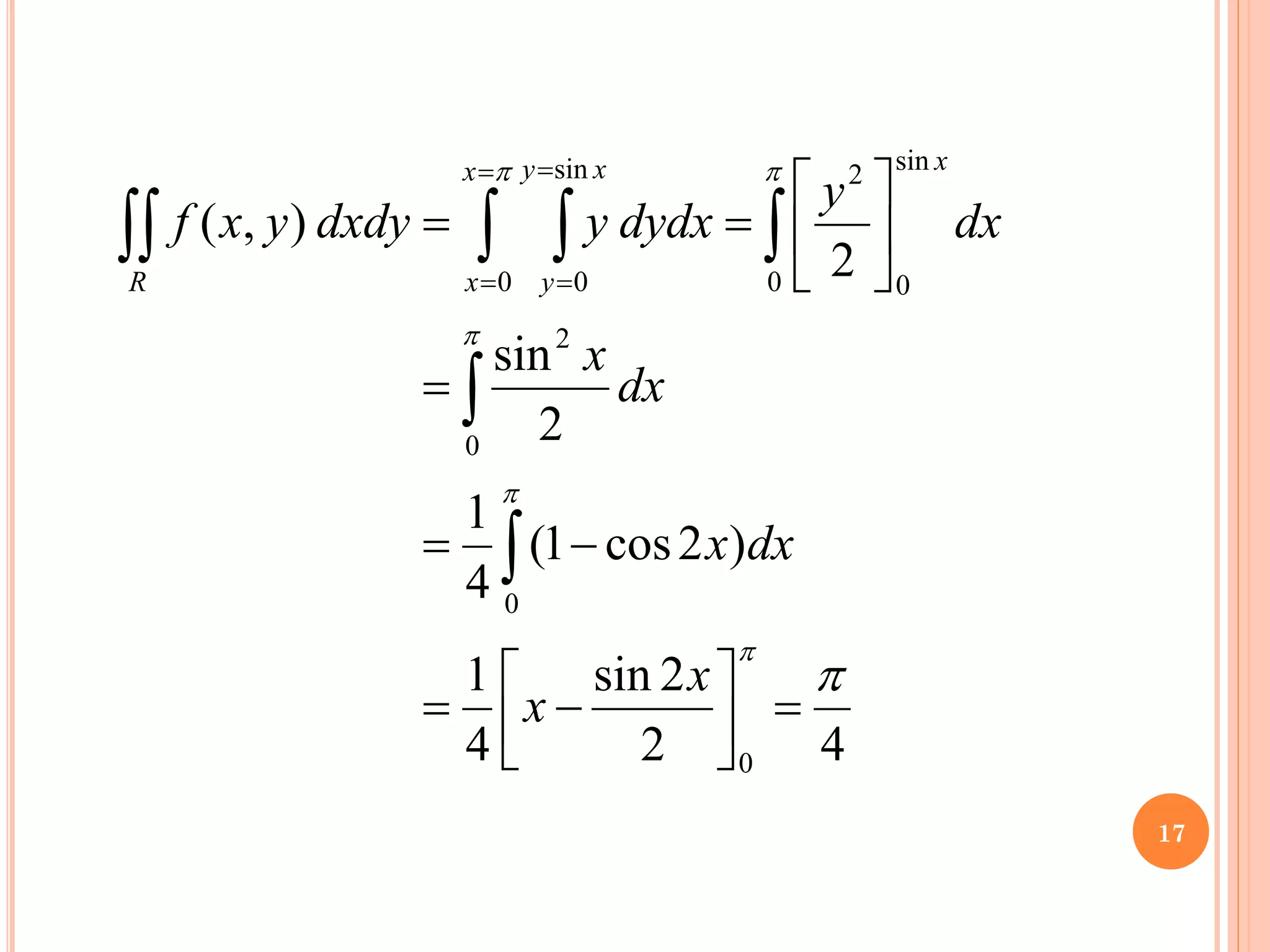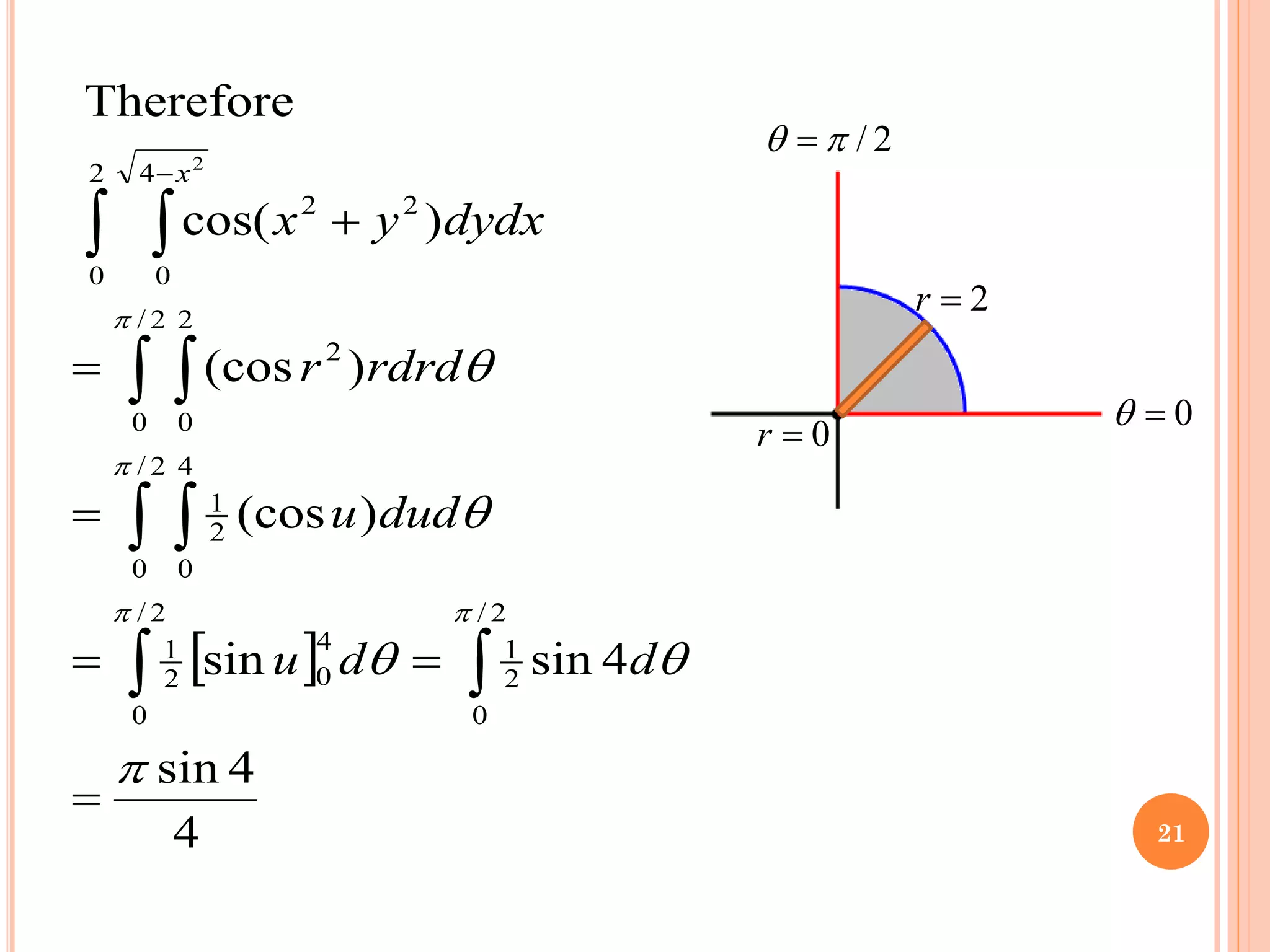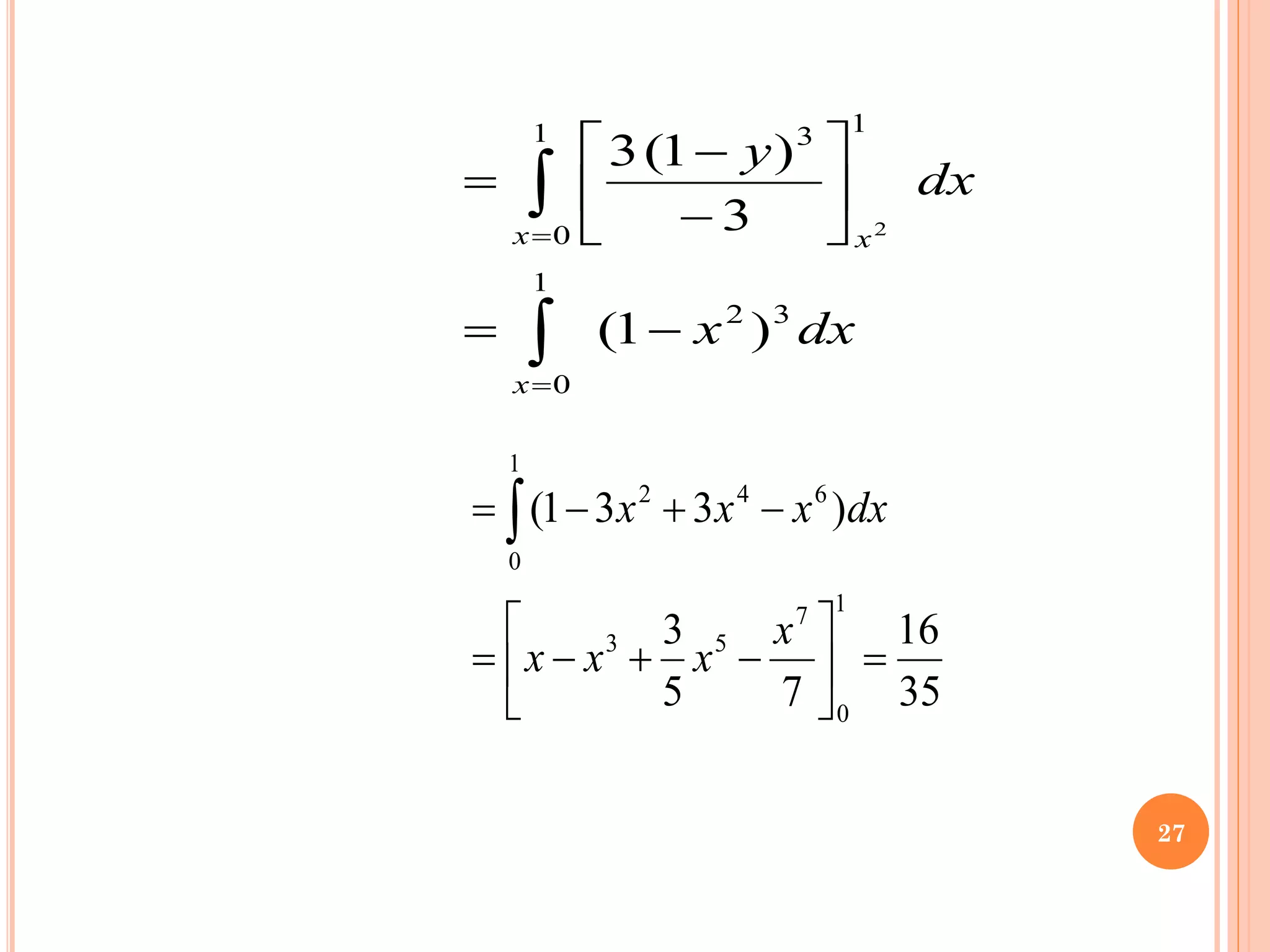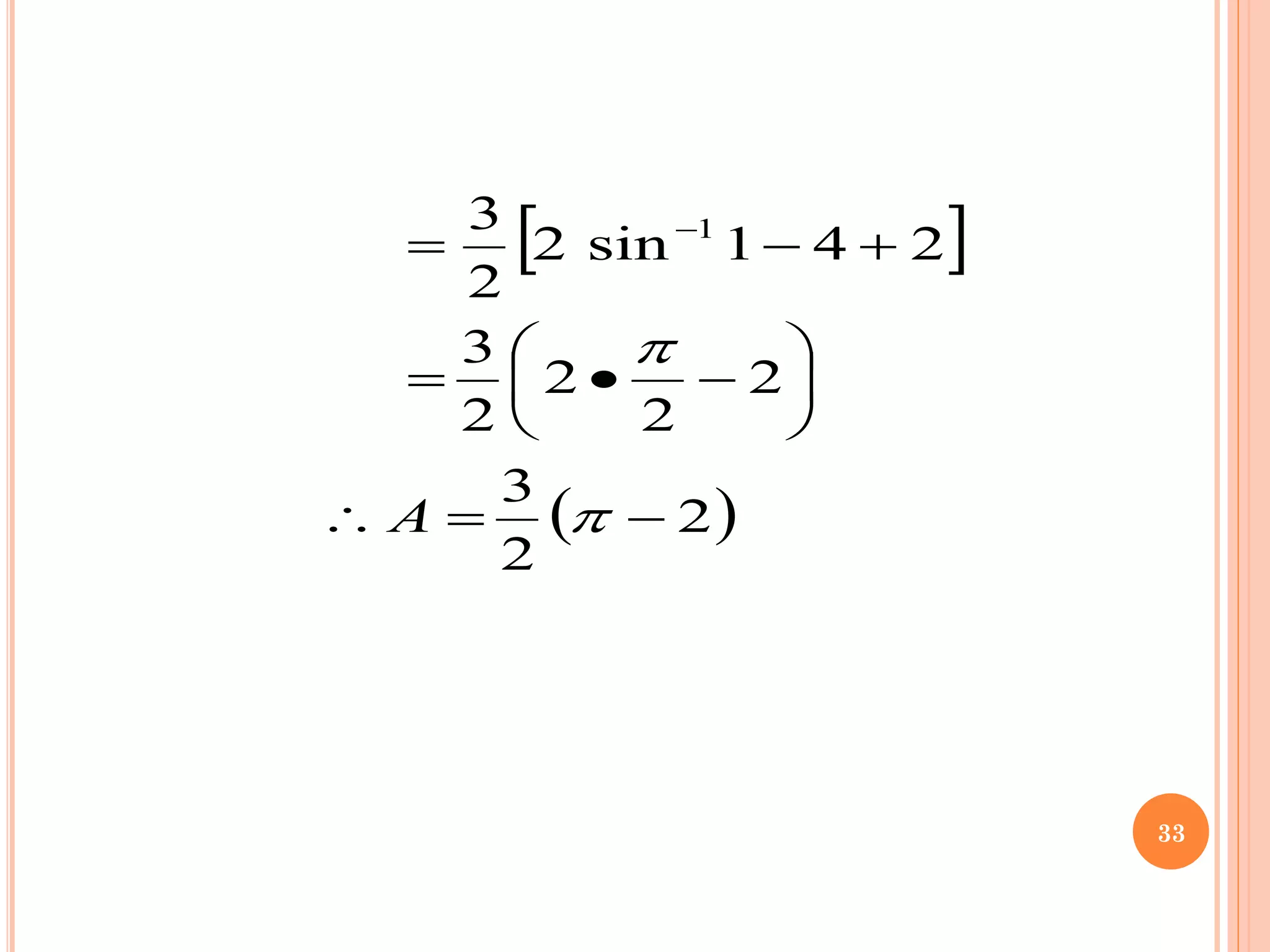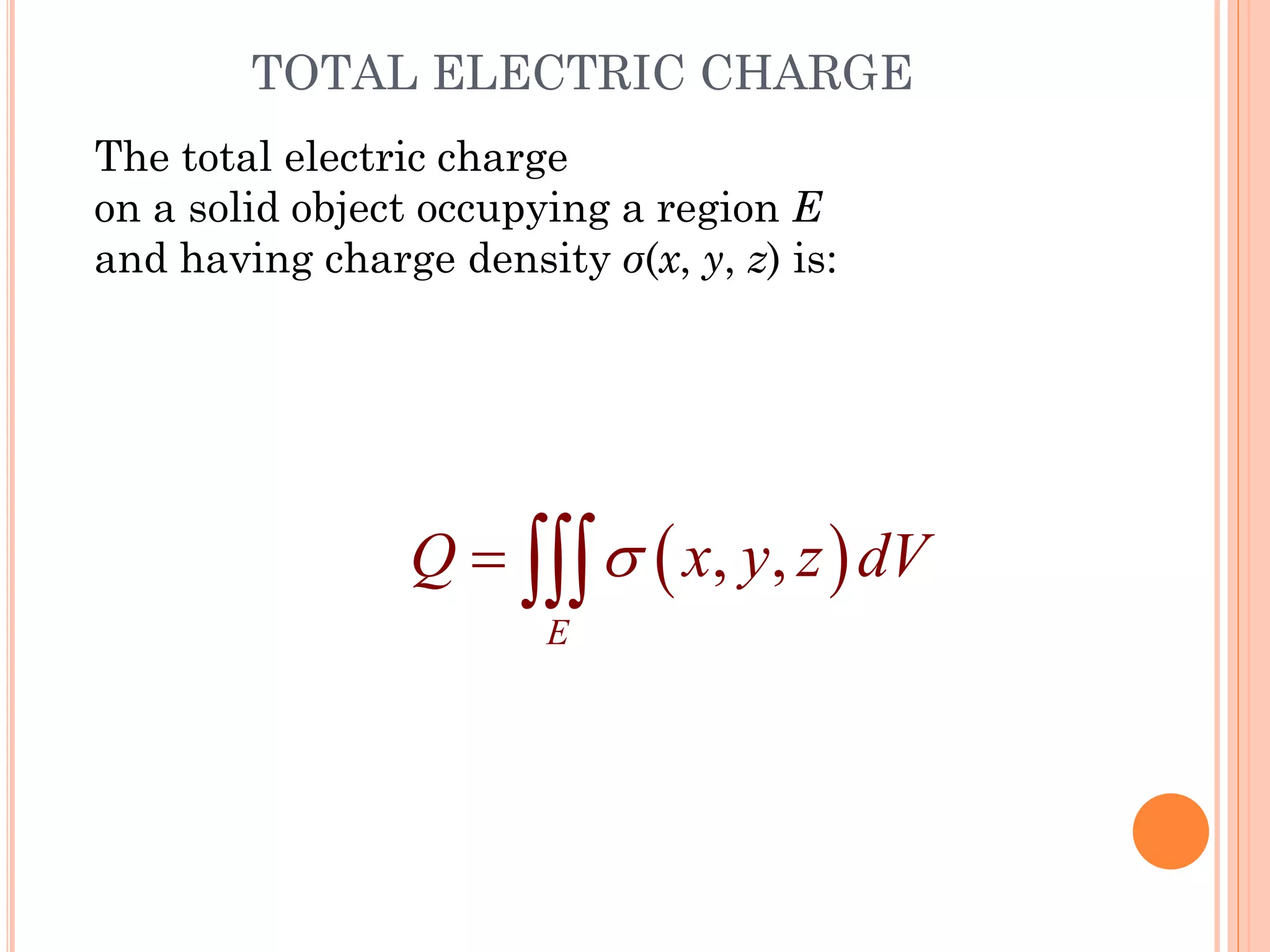The document discusses multiple integrals, including double and triple integrals, and their applications in engineering, such as finding areas, volumes, and mass. It also covers techniques like changing the order of integration, and relates these integrals to fundamental theorems in vector calculus. Additionally, the document presents various examples and methods for evaluating these integrals using Cartesian and polar coordinates.






![
14
)
1
(
2
)
2
(
2
2
6
]
)
1
(
)
1
(
3
[
]
)
1
(
)
1
(
3
[
3
)
2
3
(
)
2
3
(
have
we
,
constants
are
n
integratio
of
limits
the
Since
3
3
2
1
3
2
1
2
2
1
2
2
2
2
2
1
1
1
2
2
2
1
1
1
2
2
1
1
1
2
=
−
=
=
=
−
+
−
−
+
=
+
=
+
=
+
=
−
=
=
=
=
−
=
−
x
dx
x
dx
x
x
x
x
dx
xy
y
x
dx
dy
xy
x
dydx
xy
x
y
y
x
x
y
y
13](https://image.slidesharecdn.com/appliedmathematicsmultipleintegrationbymrs-220628064913-195df68e/75/Applied-Mathematics-Multiple-Integration-by-Mrs-Geetanjali-P-Kale-pdf-13-2048.jpg)
![
5
36
5
2
4
2
)
2
6
(
]}
)
(
2
[
]
2
)
2
(
2
{[
2
)
4
(
)
4
(
2
0
5
4
3
2
0
4
3
2
2
0
3
2
2
2
2
2
0
2
2
2
0
2
2
2
=
−
+
=
−
+
=
−
−
−
=
−
=
−
=
−
=
=
=
=
=
=
y
y
y
dy
y
y
y
dy
y
y
y
y
dy
xy
x
dxdy
y
x
dxdy
y
x
y
x
y
x
y
y
y
x
y
x
R
15](https://image.slidesharecdn.com/appliedmathematicsmultipleintegrationbymrs-220628064913-195df68e/75/Applied-Mathematics-Multiple-Integration-by-Mrs-Geetanjali-P-Kale-pdf-15-2048.jpg)