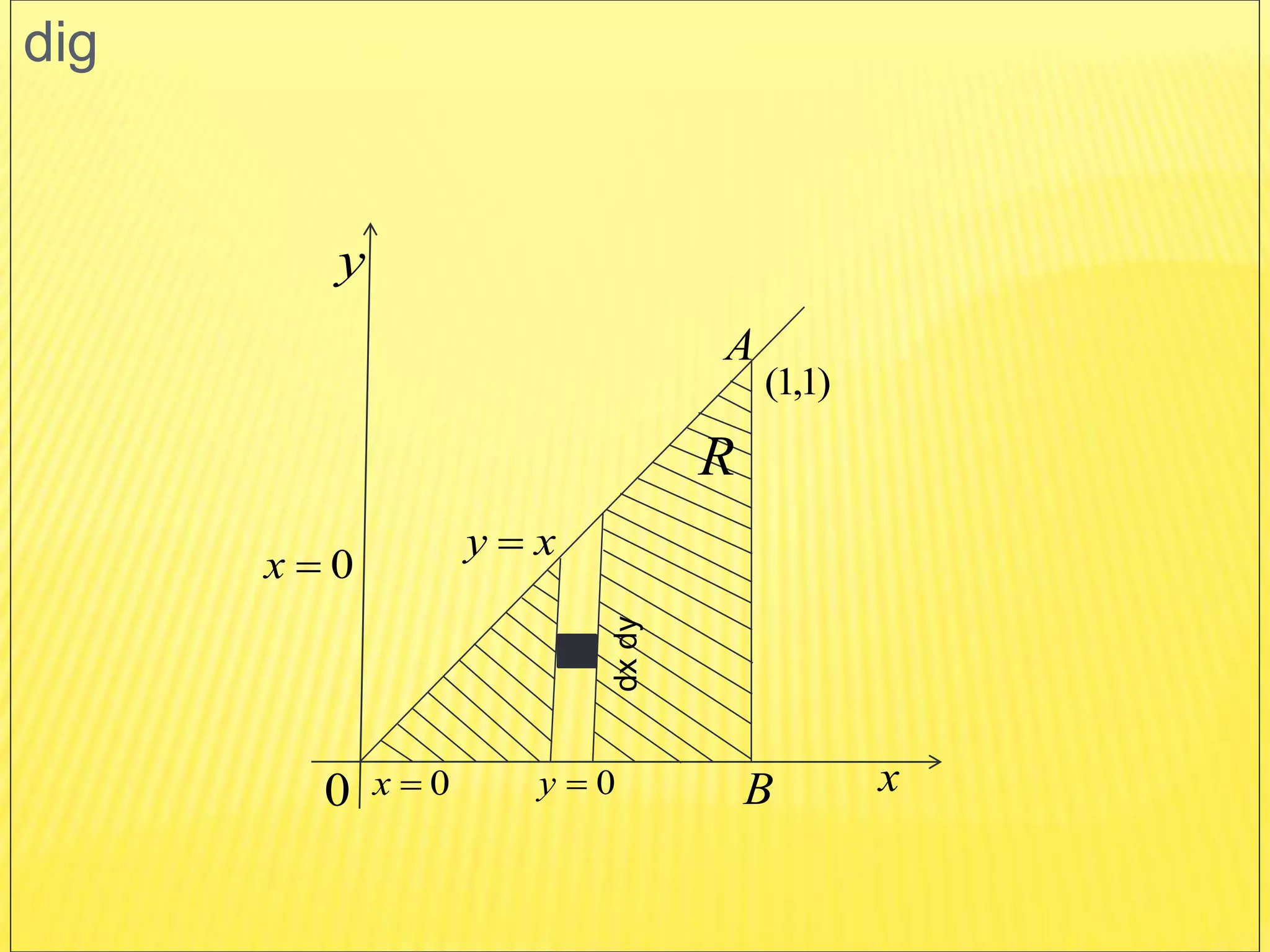
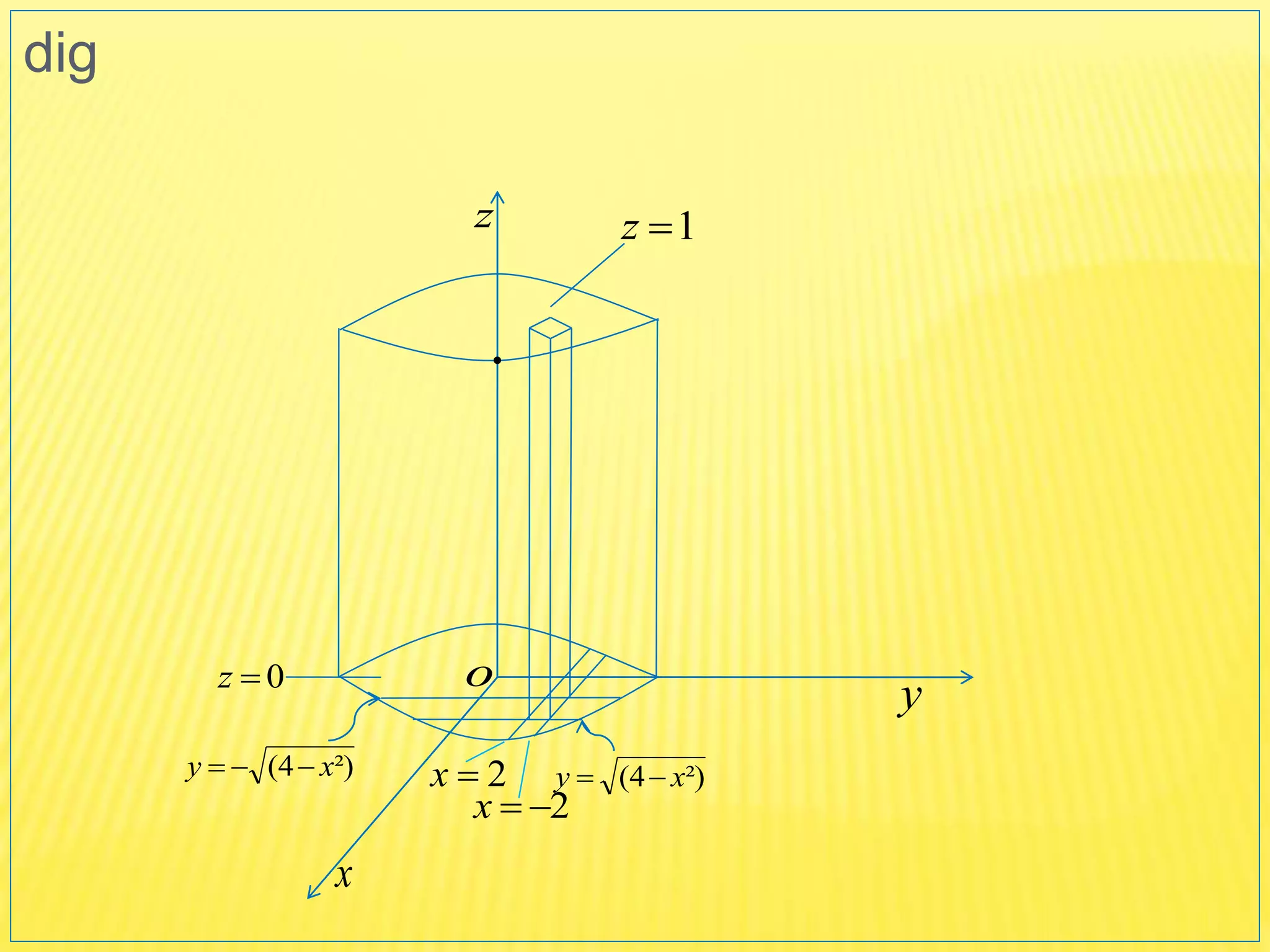
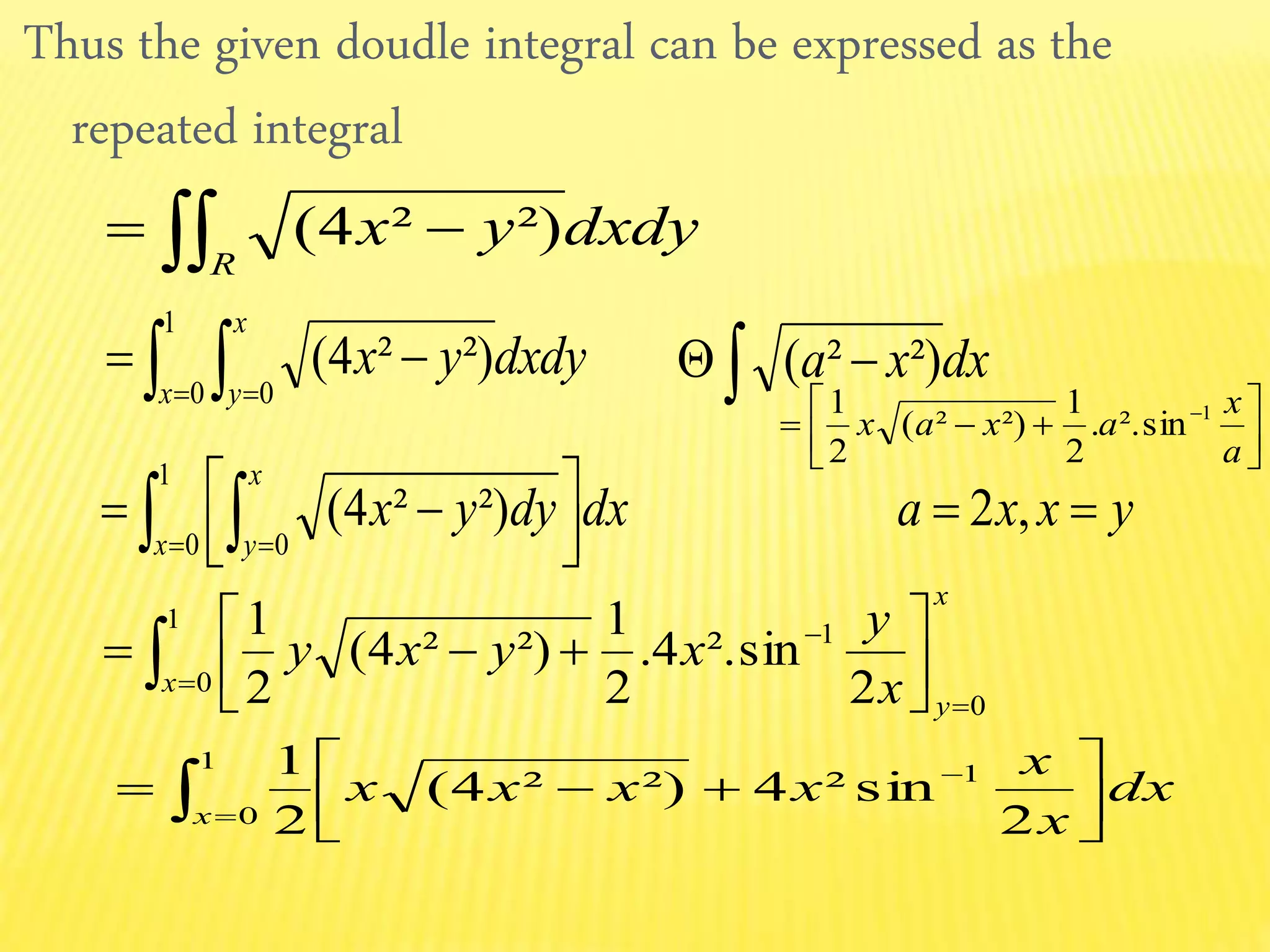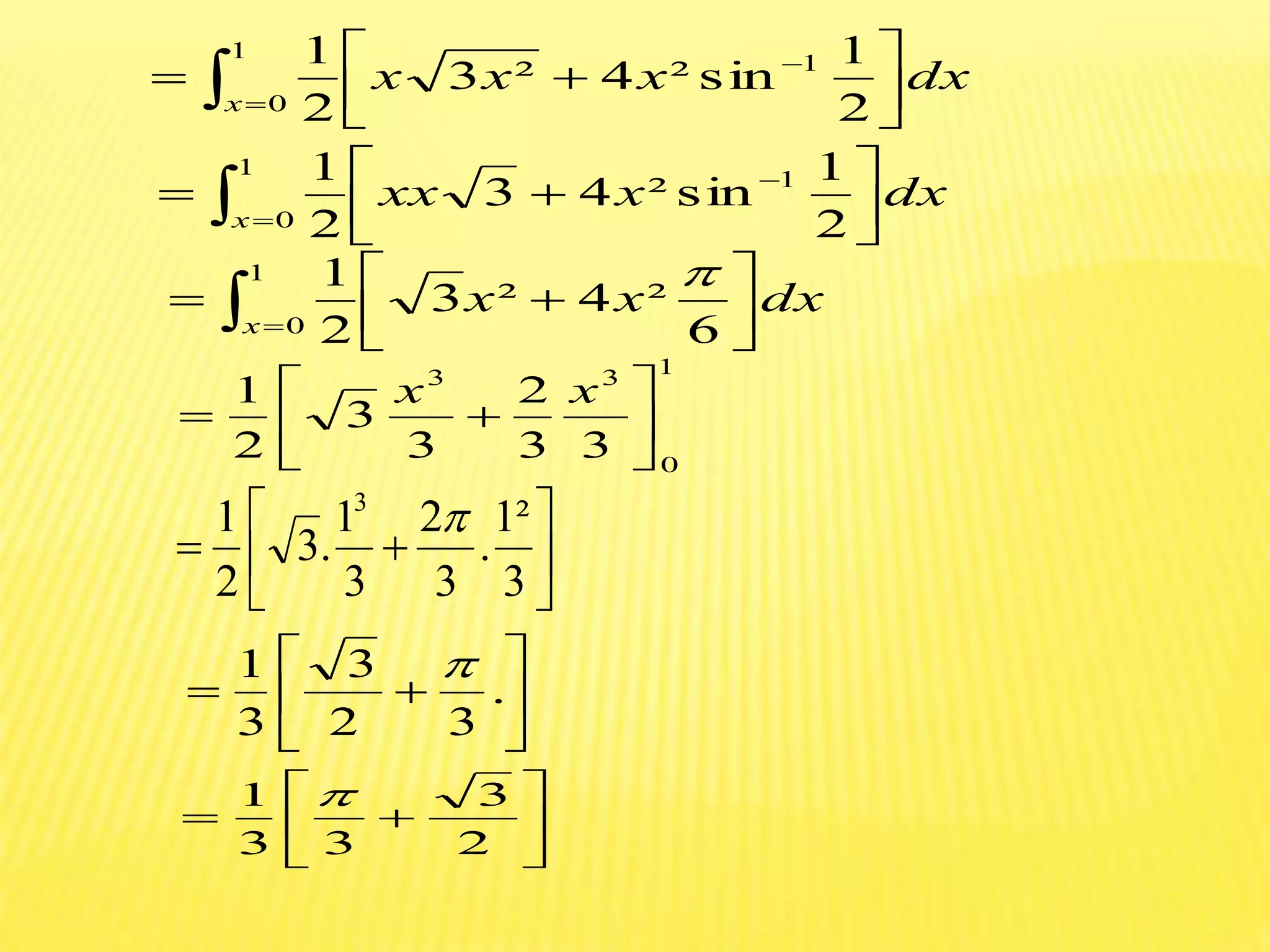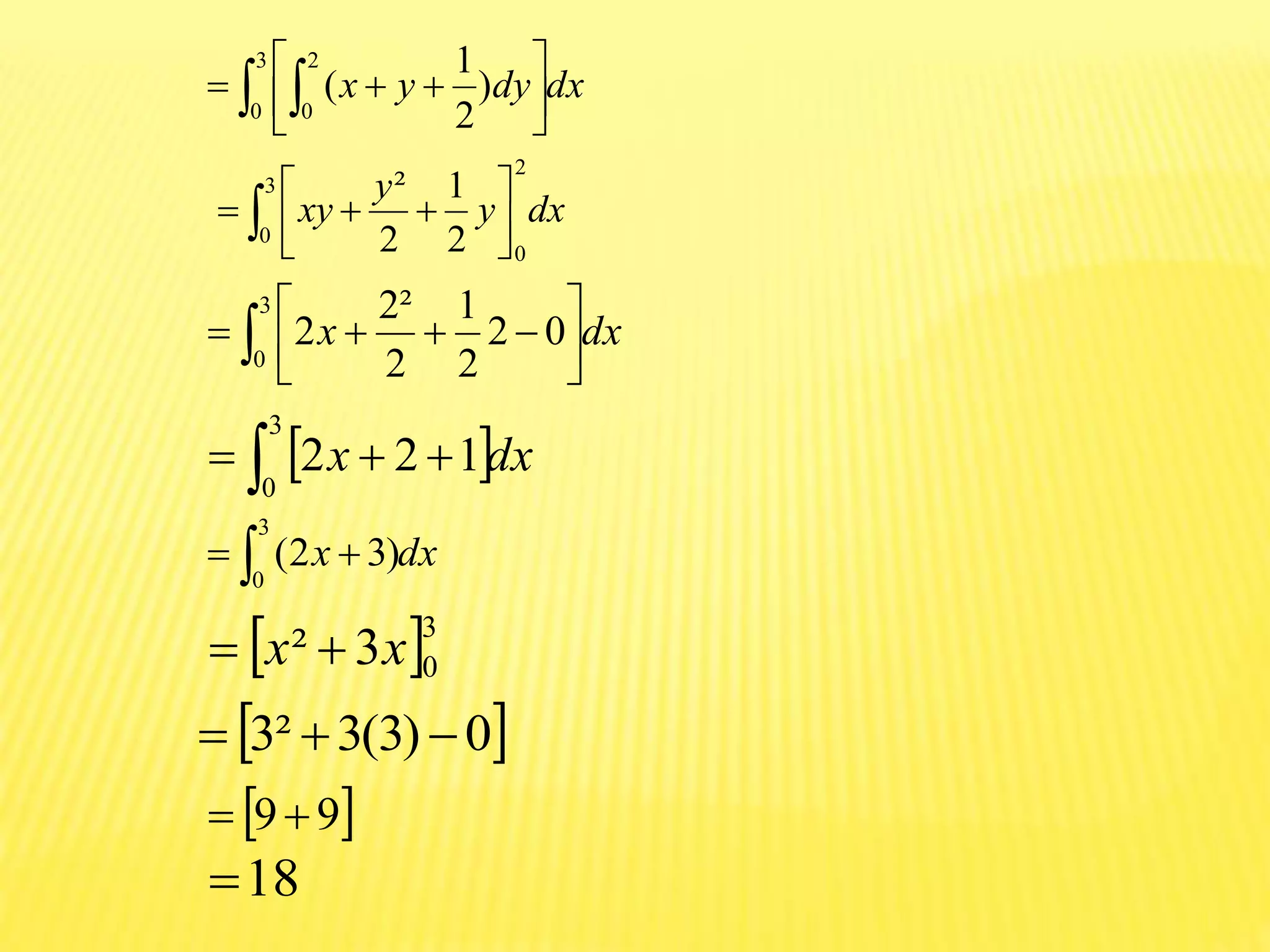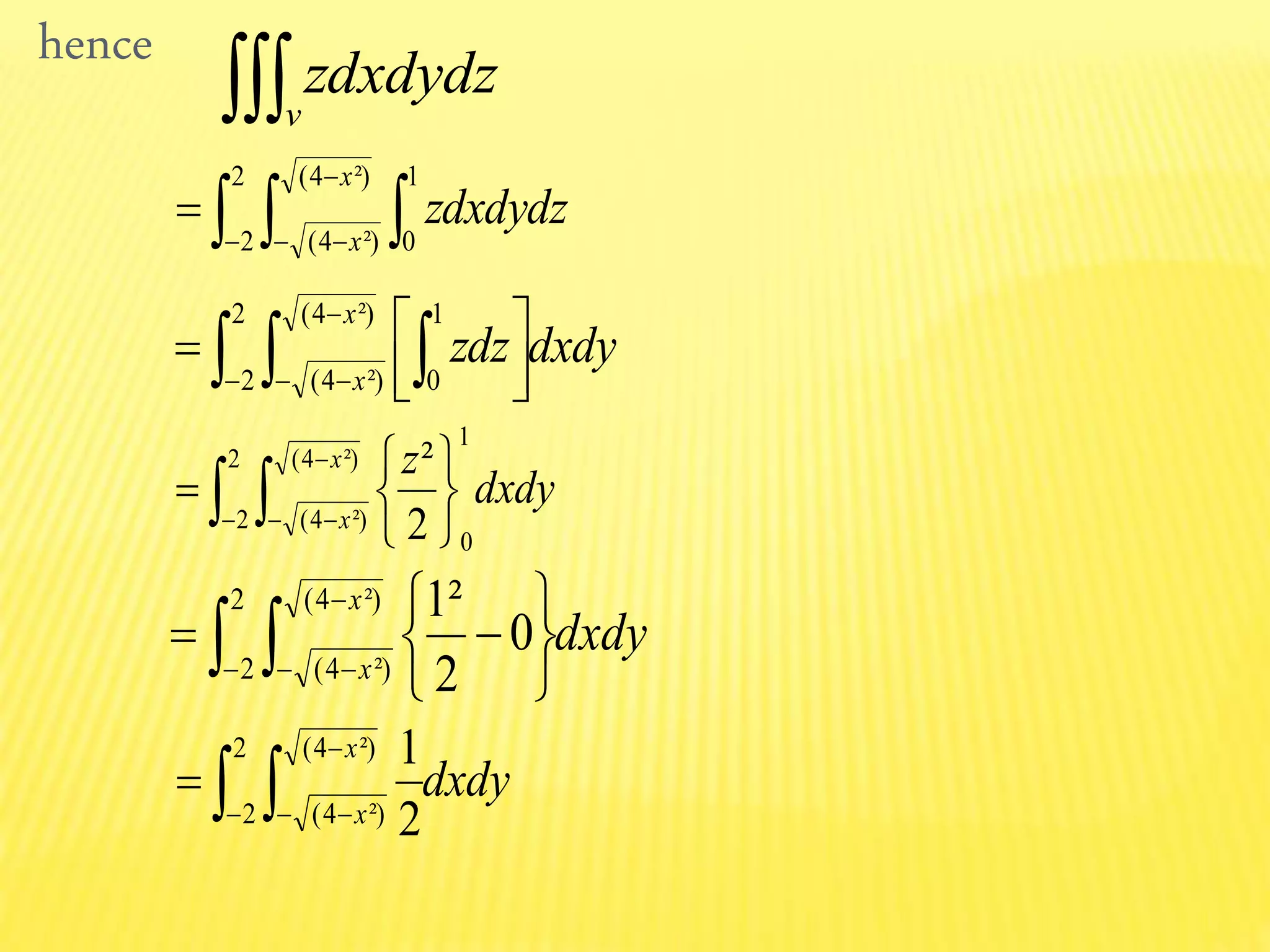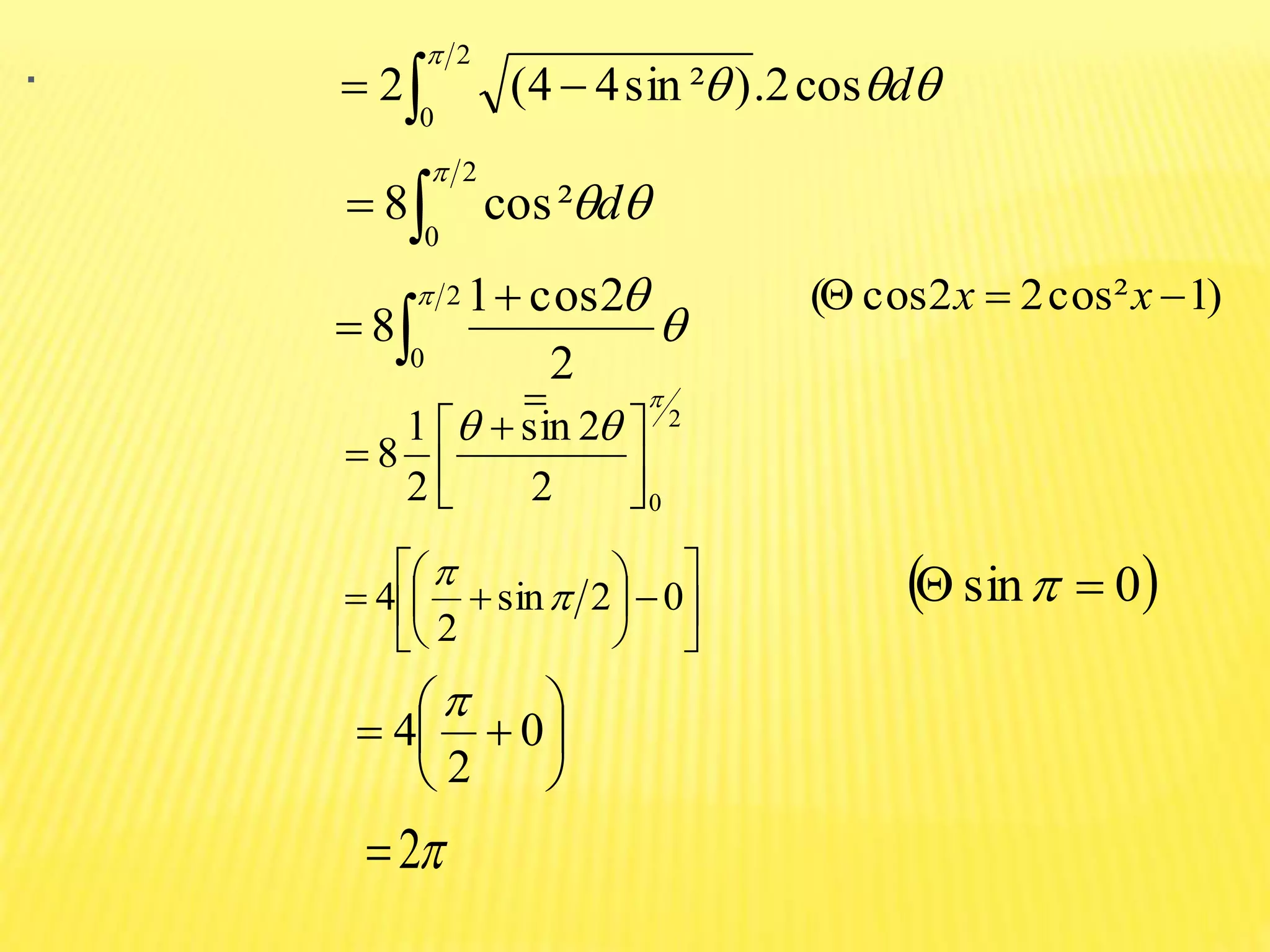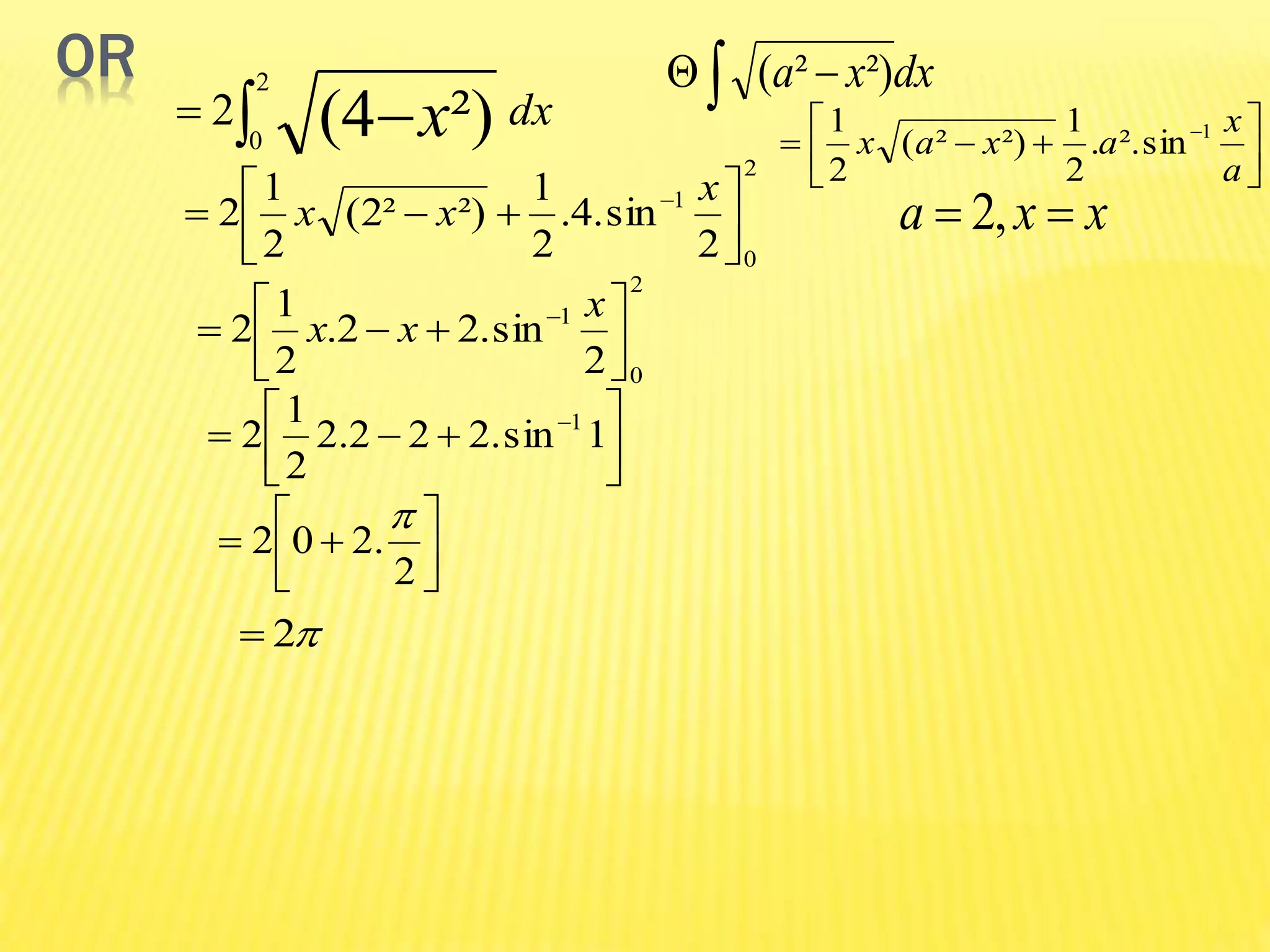The document discusses the concepts of double and triple integrals in calculus, extending the idea of definite integrals from single-variable functions to multi-variable functions. It defines double and triple integrals, outlines their properties, and provides examples demonstrating their evaluation. The document serves as an introduction to understanding integrals over multiple dimensions.

1. “ DOUBLE AND TRIPLE INTEGRAL”

2. INTRODUCTION
DEFINE DOUBLE INTEGRALS
PROPERTIES OF DOUBLE INTEGRALS
EXAMPLE OF DOUBLE INTEGRALS
DEFINE TRIPLE INTEGRALS
EXAMPLE OF TRIPLE INTEGRALS
index

3. Introduction:-
In elementary calculus, students have studied the
definite integral of a function of one variable . In this
chapeter we show how the notion of the definite integral
can be extended to functions of several variables. In
particular, we shall discuss the double integral of a
functions of two variable and the triple integral of a
function of three variables.

4. Define double integrals:-
Let f(x,y) be a function of two independent
variables x,y in - plane defined at all points in a finite
region A. let the region A be divided into n subregions
(k=1,2,…,n) of areas
let be any point inside the kth element
Let us form the sum
let us the number of subdivision becomes
infinite in such a way that the dimensions of each subdivision
approaches to zero.
kR nAAA  ,....,, 21
 kk  , kR


n
k
kkk Af
1
),( 
xy

5. If under these conditions, the limit
which is independent of the way in which the point
are chosen exists, then this limit is called the double
integral of over the region A, written
is defined by



n
k
kkk
n
Af
1
),(lim 
 kk  ,
),( yxf
A
dxdyyxf ),(
kk
n
k
k
A n
Afdxdyyxf   

),(lim),(
1


6. Properties of double integral:-
if f and g are continuous over the bounded
region R, then:
where R is composed of two subregions R1 and
R2 or
 
R R
dAyxfkdAyxkfP ),(),(.
1
    
R RR
dAyxgdAyxfdAyxgyxfP ),(),(),(),(.2
  
R R R
dAyxfdAyxfdAyxfP 1 23
),(),(),(.
  

21 1 2
),(),(),(
RR R R
dAyxfdAyxfdAyxf
dxdydA 

7. Example of double integrals:-
1. evaluate:
sol:-
  
1
0
2
0
.)( dxdyyx
dx
y
xy
2
0
1
0 2
²
 




 
1
0
)22( dxx
  
1
0
2
0
.)( dxdyyx
 1
02² xx 
 0)21( 
3

8. Example 2- when the region of integration R is the triangle
bounded by y= 0, y= x and x = 1 , show that
sol. The region of interation is shown shaded in the
adjoining figure. Let us divide the triangle OAB into
vertical strips. Then it is evident that in an elementary
strips y varies from y = 0 to y = x while x varies from
x = 0 to x = 1
).
2
3
3
(
3
1
²)²4( 

R
dxdyyx

9. dig
x
y
A
)1,1(
xy 
0x
0 0x 0y
R
B
dxdy

10. Thus the given doudle integral can be expressed as the
repeated integral
dxdyyx
R  ²)²4(
dxdyyx
x
x
y  

1
0 0
²)²4(
x
y
x x
y
xyxy
0
1
0
1
2
sin².4.
2
1
²)²4(
2
1



 






dx
x
x
xxxx
x 



 
 2
sin²4²)²4(
2
1 1
1
0




 
a
x
axax 1
sin²..
2
1
²)²(
2
1  dxxa ²)²(
   


 
1
0 0
²)²4(
x
x
y
dxdyyx yxxa  ,2

11. 





 .
32
3
3
1 







3
²1
.
3
2
3
1
.3
2
1 3

dxxxx
x 



 
 2
1
sin²4²3
2
1 1
1
0
dxxxx
x 



 
 2
1
sin²43
2
1 1
1
0
dxxx
x 



   6
²4²3
2
11
0

1
0
33
33
2
3
3
2
1







xx







2
3
33
1 

12. DEFINE TRIPLE INTEGRALS0:-
Let be a function
of three independent variables x,y,z defined for all points
in a finite closed three dimensional region V of space.
Divide V into n sub- regions of volumes , k= 1,2,….,n.
let us select an arbitrary point in each
and form the sum
let the number of sub-division become infinite in such a
way that the maximum dimensions of each
approaches to zero.
 zyxf ,,
kV)( ,, kkkkP 
kV
k
n
k
kkk V1
,, )( 
kV

13. If under these conditions, the limit
Exists, which is independent of the way in which the points
are chosen, then this limit is called the triple
integral of over the region V, written
is defined by
kkk
n
k
k
n
Vf 
)( ,
1
,lim 
)( ,, kkk 
),,( zyxf
,),,( dVzyxf
v
dVzyxf
v ),,(



n
k
kkkk
n
Vf
1
, )(lim 

14. Example of triple integrals:-
(1).Evaluate:
Sol:- let the given triple integral be denoted by . Then
   
3
0
2
0
1
0
)( dxdydzzyx
I
   
3
0
2
0
1
0
)( dxdydzzyxI
dxdydzzyx   


 
3
0
2
0
1
0
)(
dxdy
z
yzxz  




3
0
2
0
1
02
²
dxdyyx  




3
0
2
0
0
2
²1

15. dxdyyx  




3
0
2
0
)
2
1
(
dxy
y
xy 




3
0
2
02
1
2
²
dxx 
3
0
)32(
dxx 




3
0
02
2
1
2
²2
2
 dxx 
3
0
122
 3
03² xx 
 0)3(3²3 
 99
18

16. (2).evaluate:-
where the region of integration V is a cylinder,which is
bounded by the following surfaces:
z = 0, z = 1,x²+y² = 4
Sol:-
form the adjoining figure it is evident that in the region
of integration V, z varies from z = 0 to z = 1, y varies from
y = to y = and x varies from x = -2 to
x = 2
dxdydzz
v
²)4( x ²)4( x

17. dig
1zz
2x
0z o
²)4( xy  ²)4( xy 
x
y
2x


18. hence
v
zdxdydz
  



2
2
²)4(
²)4(
1
0
x
x
zdxdydz
dxdyzdz
x
x  

 



2
2
²)4(
²)4(
1
0
dxdy
zx
x 









2
2
²)4(
²)4(
1
02
²
dxdy
x
x 









2
2
²)4(
²)4(
0
2
²1
dxdy
x
x 



2
2
²)4(
²)4( 2
1

19. dxdy
x
x 

 



2
2
²)4(
²)4(
1
2
1
  dxy
x
x



2
2
²)4(
²)4(2
1
 dxxx 

2
2 ²)4(²)4(2
1
dxx 

2
2 ²)4(22
1
dxx 
2
0 ²)4(2
dxx²)4(  Is an even
function,so
 

a
a
a
dxxfdxxf
0
)(2)(
On substituting so thatsin2x ,cos2 ddx 


dcos2.)²sin44(2
2
0 
dxdy
x
x 



2
2
²)4(
²)4(
1
2
1

20. .

2
0
²cos8

d



2
0 2
2cos1
8



2
02
2sin
2
1
8





 


)1²cos22cos(  xx












 02sin
2
4 







 0
2
4

2
 0sin 


dcos2.)²sin44(2
2
0 

21. OR
dxx 
2
0 ²)4(2   dxxa ²)²(




 
a
x
axax 1
sin²..
2
1
²)²(
2
1
xxa  ,2
2
0
1
2
sin.4.
2
1
²)²2(
2
1
2 



  x
xx
2
0
1
2
sin.22.
2
1
2 



  x
xx




 
1sin.222.2
2
1
2 1





2
.202

2

22. THANK YOU