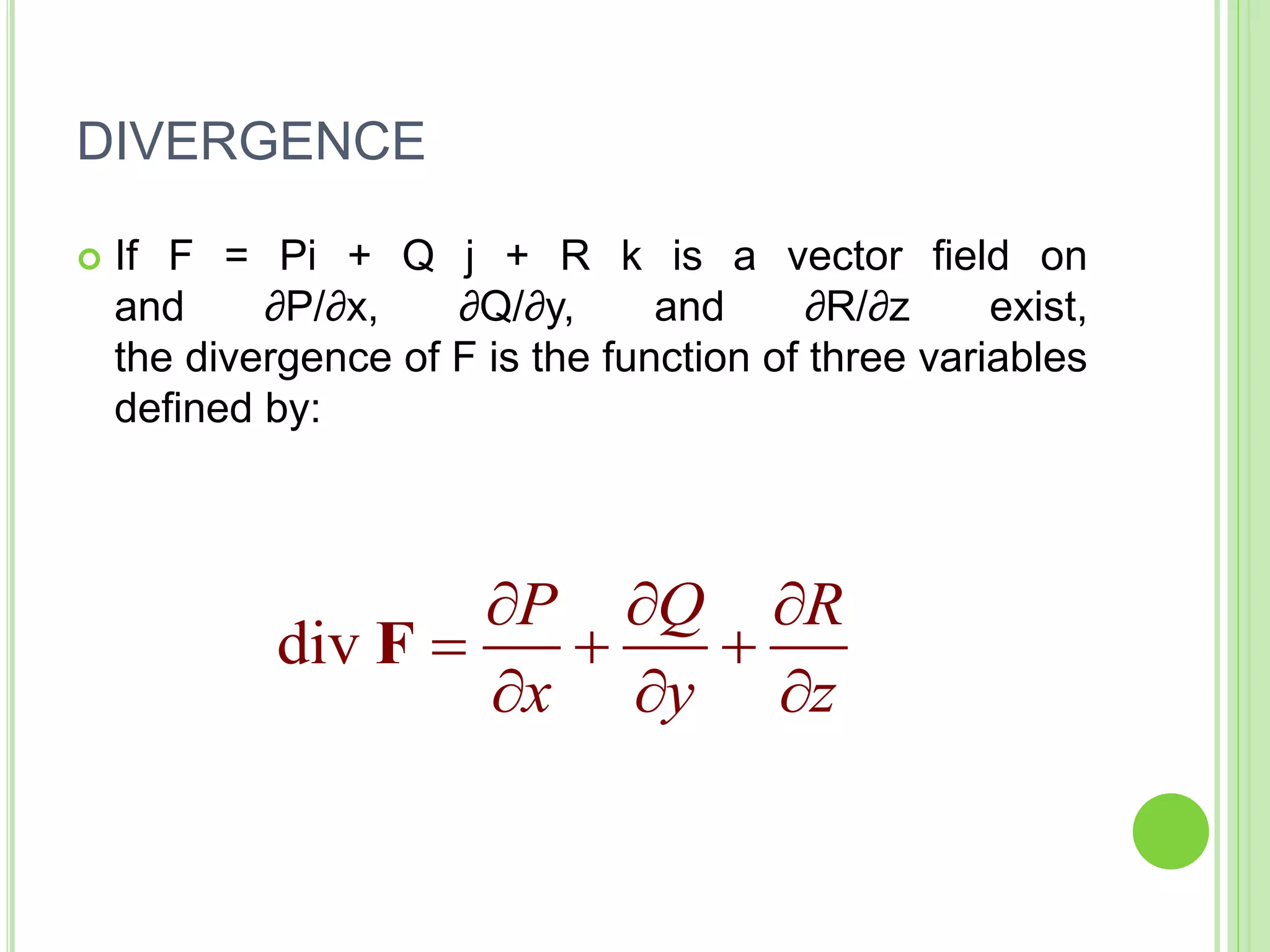This document provides an overview of key concepts in vector calculus and linear algebra, including: - The gradient of a scalar field, which describes the direction of steepest ascent/descent. - Curl, which describes infinitesimal rotation of a 3D vector field. - Divergence, which measures the magnitude of a vector field's source or sink. - Solenoidal fields have zero divergence, while irrotational fields have zero curl. - The directional derivative describes the rate of change of a function at a point in a given direction.

1. VECTOR CALCULUS AND LINEAR
ALGEBRA
Presented by:-
Hetul Patel- 1404101160
Jaina Patel - 1404101160
Kinjal Patel - 1404101160
Kunj Patel -1404101160
Matangi Patel -1404101160

2. CONTENTS
 PHYSICAL INTERPRETATION OF GRADIENT
 CURL
 DIVERGENCE
 SOLENOIDAL AND IRROTATIONAL FIELDS
 DIRECTIONAL DERIVATIVE

3. GRADIENT OF A SCALAR FIELD
 The gradient of a scalar function f(x1, x2, x3, ..., xn) is
denoted by ∇f or where ∇ (the nabla symbol) denotes the
vector differential operator, del. The notation "grad(f)" is
also commonly used for the gradient.
 The gradient of f is defined as the unique vector field
whose dot product with any vector v at each point x is the
directional derivative of f along v. That is,
 In 3-dimensional cartesian coordinate system it is
denoted by:
f f f
f
x y z
f f f
x y z
  
   
  
  
  
  
i j k
i j k

4. PHYSICAL INTERPRETATION OF
GRADIENT
 One is given in terms of the graph of some
function z = f(x, y), where f is a reasonable
function – say with continuous first partial
derivatives. In this case we can think of the
graph as a surface whose points have
variable heights over the x y – plane.
 An illustration is given below.
If, say, we place a marble at some point
(x, y) on this graph with zero initial force, its
motion will trace out a path on the surface,
and in fact it will choose the direction of
steepest descent.
 This direction of steepest descent is given
by the negative of the gradient of f. One
takes the negative direction because the
height is decreasing rather than increasing.

5. PHYSICAL INTERPRETATION OF
GRADIENT
 Using the language of vector fields, we may restate
this as follows: For the given function f(x, y),
gravitational force defines a vector field F over the
corresponding surface z = f(x, y), and the initial
velocity of an object at a point (x, y) is given
mathematically by – ∇f(x, y).
 The gradient also describes directions of maximum
change in other contexts. For example, if we think
of f as describing the temperature at a point (x, y),
then the gradient gives the direction in which the
temperature is increasing most rapidly.

6. CURL
 In vector calculus, the curl is a vector operator that
describes the infinitesimal rotation of a 3-
dimensional vector field.
 At every point in that field, the curl of that point is
represented by a vector.
 The attributes of this vector (length and direction)
characterize the rotation at that point.
 The direction of the curl is the axis of rotation, as
determined by the right hand rule, and the
magnitude of the curl is the magnitude of that
rotation.

7. CURL
 Definition:
 It is also defined as:

8. POINTS TO BE NOTED:
 If curl F=0 then F is called an irrotational vector.
 If F is irrotational, then there exists a scalar point
function ɸ such that F=∇ɸ where ɸ is called the
scalar potential of F.
 The work done in moving an object from point P to
Q in an irrotational field is
= ɸ(Q)- ɸ(P).
 The curl signifies the angular velocity or rotation of
the body.

9. DIVERGENCE
 In vector calculus, divergence is a vector operator
that measures the magnitude of a vector
field's source or sink at a given point, in terms of a
signed scalar.
 More technically, the divergence represents the
volume density of the outward flux of a vector field
from an infinitesimal volume around a given point.

10. DIVERGENCE
 If F = Pi + Q j + R k is a vector field on
and ∂P/∂x, ∂Q/∂y, and ∂R/∂z exist,
the divergence of F is the function of three variables
defined by:
div
P Q R
x y z
  
  
  
F

11. DIVERGENCE
 In terms of the gradient operator
 The divergence of F can be written symbolically as the dot
product of and F:
x y z
                   
i j k
div  F F

12. SOLENOIDAL AND IRROTATIONAL
FIELDS
 The with null divergence is called solenoidal, and
the field with null-curl is called irrotational field.
 The divergence of the curl of any vector field A must
be zero, i.e.
∇· (∇×A)=0
 Which shows that a solenoidal field can be
expressed in terms of the curl of another vector
field or that a curly field must be a solenoidal field.

13. SOLENOIDAL AND IRROTATIONAL FIELDS
 The curl of the gradient of any scalar field ɸ must
be zero , i.e. ,
∇ (∇ɸ)=0
 Which shows that an irrotational field can be
expressed in terms of the gradient of another scalar
field ,or a gradient field must be an irrotational field.

14. DIRECTIONAL DERIVATIVE
 The directional derivative is the rate at which the
function changes at a point in the direction . It is a
vector form of the usual derivative, and can be
defined as:-
=
=
Where ▼ is called "nabla" or "del"
and denotes a unit vector.